Спектральные свойства нелинейных поверхностных поляритонов среднего ИК-диапазона в структуре «полупроводник - слоистый метаматериал»

Поверхностные поляритоны (ПП) на границах нелинейных и линейных сред являются объектом активных исследований [1 –4]. Области применения поверхностных поляритонов обширны: это оптическое хранение данных, биосенсоры, генерация и управление светом, схемы фотоники, солнечные элементы и т.д. [5, 6].

Нелинейным ПП свойственны замечательные особенности, не встречающиеся в линейной теории, например, существование ТМ-поляритонов, распространяющихся вдоль границы сред с диэлектрическими проницаемостями одного знака, нелинейное просветление для волн большой мощности в непрозрачной среде, наличие пространственных поверхностных плазмон-солитонов, т.е. недифрагирующих самолокализованных поверхностных волн [7]. В ряде случаев электромагнитное поле поверхностного поляритона может существенно превышать поле падающего света, например, на металлической и рельефной поверхности, в системах с неупорядоченными средами при низких температурах. Усиление поля поверхностного поляритона может происходить при нелинейных оптических явлениях, которые зависят от интенсивности возбуждающей световой волны, в частности, при усиленном поверхностью комбинационном рассеянии, генерации второй гармоники, нелинейности Керра, самофокусировке электромагнитного поля и т.д. Несмотря на немалое количество научных публикаций в этой области, 1D-структуры с нелинейными ПП продолжают оставаться в фокусе внимания исследователей. Так, нелинейные ПП TE- и TM-поляризаций на границе «левая среда – диэлектрик»

рассмотрены в статье Шадривова и др. [8], а распространение TE-волн вдоль поверхности нелинейного диэлектрика с графеновым покрытием исследованы в работе [9]. Рассматриваемая структура, кроме нелинейности и гиротропных свойств, обладает ещё и наноструктурированностью, приводящей, например, к анизотропии ТЕ- и ТМ-волн [10] в направляющей 4слойной структуре, что нетипично для волноводов на основе традиционных (однородных) сред.

В недавних работах авторов [11, 12] приведён подробный обзор использования нелинейных ПП в различных областях физики и техники, а также рассмотрены нелинейные ПП в направляющей системе на основе полупроводника и нанокомпозитной среды – слоистого метаматериала (СМ).

В настоящей статье, являющейся продолжением указанных работ, проводится сравнение аналитических методов описания направляющих систем с нелинейным откликом (т.е. «одноосного» и «двуосного» приближений), и на основе полученных результатов рассматриваются возможности эффективного управления дисперсией нелинейных ПП.

1.    Постановка задачи

Рассмотрим структуру, в которой ось x перпендикулярна границе раздела сред, область x < 0 занимает гиротропный СМ на основе чередующихся слоёв висмут-содержащего феррит-граната (BLIG, Lu3-x Bix Fe5-y Gay O12) и гадолиний-галлиевого граната (GGG, Gd3Ga5O12). В области x >0 располагается полупроводник (n-InSb), обладающий кубической нелинейностью третьего порядка. Будем считать, что электромагнитная волна распространяется вдоль оси z, а вектор намагниченности M поперечен направлению распространения волны и направлен вдоль оси y (рис. 1). Электрическое и магнитное поля волны при этом имеют гармонические зависимости вида exp[i (ωt – βz)], где i – мнимая единица, ω – частота излучения, t – время, β – константа распространения,

z – координата.

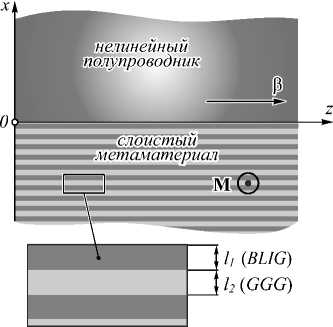
Рис. 1. Геометрия структуры

Для выбранных материалов собственными волнами рассматриваемой структуры являются ТМ- и ТЕ-волны поляритонного типа, имеющие компоненты напряженностей электрического и магнитного полей ( h x , e y , h z ) и ( e x , h y , e z ) соответственно. Далее будет рассматриваться случай ТМ-поляризации, представляющий б о льшую сложность для описания, нежели случай ТЕ-волн [13].

2. Волновые поля в слоистом метаматериале

СМ состоит из чередующихся слоёв тонких плёнок BLIG и слоёв галлий-гадолиниевой подложки с толщинами слоёв l 1 и l 2 и тензорами диэлектрической проницаемости (ДП) ε ˆ _BIG и ε ˆ _GGG соответственно:

ε ˆ _GGG = I ˆ ε ₂ , ε ˆ _BIG = I ˆ ε ₁ - ie_ijk ε _a , (1) где I ˆ – единичный тензор, а e ijk – тензор Леви–Чевиты.

Для описания отклика СМ на внешнее электромагнитное поле необходимо провести усреднение ДП по составляющим его слоям. После процедуры усреднения, описанной в [14], тензор эффективной ДП многослойной нанокомпозитной среды запишется в виде:

/х εef

( £ ε _xx

I ^e z,

ε yy 0

£

.

^e zz J

Здесь компоненты тензора

ε xx

ε ₁ ε ₂ ( Θ+ 1)         Θε ₁ +ε ₂

, ε= ,

Θε ₂ +ε ₁      ^yy Θ+ 1

ε

Θ+ 1

ε ²

- ^a ) +ε 2 + ε ₁

Θε ² _a ε ₂

e i ( 0£ 2 +e i ) J

ε

xz

-

ε

zx

i Θε _a ε ₂

Θε ₂ +ε ₁ ,

где Θ = l 1 / l 2 – отношение толщин нанослоёв, составляющих СМ.

Компоненты электрического и магнитного полей ТМ-волны в СМ можно записать в следующей форме:

E_z = E_{z 0} exp( q_gx ),

H_y = ( i βε _xz -ε _xxq_g ) k ⁰ E ₂ ^z ,                           (4)

K

E_x = ( ik ₀ ² ε _xz -β q_g ) E^z ₂ ,

K

где q g и K имеют смысл поперечных волновых чисел в СМ для ТМ-волны и компонента волнового вектора, отвечающая ДП ε xx :

q g ² = ( β ² - k 0 ² ε ⊥ ) ^{ε zz} , K ² =β ² - k 0 ² ε xx , ε ⊥ =ε xx +^{ε xz} , εε xx                                                   zz

а ε ⊥ – поперечная ДП в СМ. Здесь k 0 = ω/ c – волновое число, c – скорость света в вакууме. В выбранном частотном диапазоне магнитные проницаемости СМ (и составляющих его слоёв) и полупроводника приняты равными единице.

3. Волновые поля и дисперсионное соотношение для поляритонов в структуре: полупроводник с линейным откликом

Линейная часть тензора ДП полупроводника имеет частотную зависимость, определённую с помощью модели Друде [15, 16]:

εs = ε∞ (1-ω2p/ω2), ωp = 4πne2 / m∗ε∞ , где ε∞ – высокочастотная ДП, ωp – плазменная частота, в которую входят концентрация носителей заряда n (в данном случае – электроны), заряд электрона e и его эффективная масса m*. Компоненты поля ТМ-волны в полупроводнике связаны соотношениями:

βhy =k0εsex, hy′ = ik0εsez ,                                              (5)

e_z ′ + i β e_x = ik ₀ h_y .

Здесь штрихом обозначена производная по координате x. Учёт граничных условий (при x =0) для тангенциальных компонент вектора напряжённости электрического поля и нормальных компонент вектора электрической индукции приводит к дисперсионному соотношению q q ε -iε q β+K2ε =0,                     (6)

s g xx xz s             s где qs2 = β2 - k02εs – поперечная компонента волнового вектора в линейном полупроводнике.

4. «Одноосное» (продольное) приближение

В продольном приближении тензор ДП полупроводника может быть записан в виде [2, 17]:

ε ˆ _s ( x ) =

( £ e ^

I ⁰

0      1

2 , ^e _s +X e z ⁽ x )| J

где χ – скалярная нелинейная восприимчивость 3-го порядка. Тогда компоненты поля ТМ-волны связываются соотношениями:

e hy = k0£ sex, hy= iko(Es + Xe2)ez,                                  (8)

e ¹ i ^e e x = ik 0 h y .

Решая систему (8), получим уравнение для продольной компоненты электрического поля в виде:

e Z '" q e z — ( X q 2 / e s ) e Z = 0.                            (9)

Уравнение (9) аналогично нелинейному уравнению Шрёдингера, а его решение формально может быть записано с помощью функции гиперболического секанса или косеканса. В случае косеканса решение на границе раздела сред ( x =0) бесконечно, поэтому касательные составляющие полей ТМ-волны в нелинейной среде запишем в виде:

ez = A • sech [qs (x - x0)], ex = -( iPA / qs)th [ qs(x—xo)]sech [ qs(x " xo)],     (10)

hy = -(ik0^ sA 1 qs) th [ qs(x—x0)] sech [ qs(x - x0)], где амплитуда A = ^-2£s IX , а параметр x0, возникающий при интегрировании уравнения (9), определяет положение максимума амплитуды электрического поля. Таким образом, в данном приближении в нелинейной среде может возникать самофокусировка поля, приобретающего вид пространственного солитона [18, 19]. При этом ПП существуют лишь в частотной области, где εs ≤ 0. Учитывая электродинамические граничные условия, получаем дисперсионное уравнение для нелинейных поверхностных ТМ-поля-ритонов:

^£ s K ²t ^h( q s x 0 ) + E xx q s q g ^- i £ xz P q s = ^{0            (11)}

• 5.    Компоненты полей и дисперсионное уравнение для ТМ-поверхностных поляритонов в «двуосном» случае нелинейности

Антимонид индия относится к кристаллографической группе 43m , поэтому с учётом кубической нелинейности тензор ДП кристалла InSb можно представить в виде [7, 20]:

£ s ( x ) = £ s + £ NL = £ s +

А

+

X 1 e x ^{( x} )|^{2 +} X 2 e z ^{( x} )|^{2                0}

₄             0               X 1 e z ( x )|² +X 2 e x ( x )|²

.

Соотношение между компонентами χ 1 и χ 2 тензора нелинейной восприимчивости может соответствовать одному или нескольким механизмам нелинейности (например, тепловой механизм, электрострикция, электронная дисторсия, молекулярный ориентационный эффект Керра и т.п.) [7, 21].

Компоненты поля ТМ-волны в полупроводнике запишутся в следующем виде:

Phy = k0(£s +X1 ex Г +X2 ez |2)ex , hy= ik0(£ s +X1 ez |2 +X2 |ex|2) ez ,                    (13)

e z ⁺ i P e x = ^ik 0 h y .

Далее для выражения отдельных компонент поля перейдём от комплексных полей к действительным, следуя [7, 20–22]:

e z = E z , e x =" iE x , h y =" iH y ,                (14)

где E x , H y , E z – вещественные величины.

Преобразуя систему (13), запишем биквадратное уравнение относительно вещественной компоненты E z :

AE_z ⁴ + ВЕ ^ + C = 0,                          (15)

где коэффициенты

A = ( k 0 I P ) ² •X 2 E x + 0,5 X 1 ,

В = 2 ( k 0 I P ) ² ^2E x ²( X 1 E x +£ s ) + £ s "X 2 E x ²,

C = [ ( k 0 I P ) ² • ( X 1 E x + £ s ) 2 "  ((3I2) X 1 E x + £ s ) ] E x '.

Уравнение (15) имеет в общем случае четыре корня, отвечающие разным сочетаниям знаков «+» и «–» перед обоими квадратными корнями:

E_z = ±V ( - В ± Bl " - 4 AC )I2 A .              (16)

Обозначим X = E x, (x ), Z = E_z ²( x ). Тогда, согласно (15), величина Z является функцией X , что даёт возможность решить обратную задачу о нахождении профильной функции E x ( x ) в полупроводнике с помощью численного интегрирования [20]:

xx d x = ¹ x т----- ^£ xx + ^{2 X 1} X ---------d Ex . (17)

^J0       p E ^J(0, V z [2 X 2 X (1 - k 0 ² £ xx I в ²) -£ zz ]

При записи граничных условий необходимо также учесть замену (14) при подстановке компонент полей ТМ-волны (4) в СМ

E z (0) + ME x (0) £ NL = 0,                        (18)

где вспомогательный параметр [12]

M = K ²( £ xx q g p- i £ xz в ²),                       (19)

а E x (0) – амплитуда электрического поля на границе в полупроводнике.

6.    Сравнительный анализ и обсуждение результатов

Для расчёта дисперсионных характеристик ПП в рассматриваемой системе в области длин волн АХ=5 ^ 20 мкм выбраны следующие параметры сред. Показатель преломления висмут-замещенного железоиттриевого граната (Lu,Bi) 3 (Fe,Ga) 5 O 12 n 1 = ^Ё? =2,33 [23], недиагональная компонента ДП ε a = 0,005 (исходя из того, что угол Фарадея в данном случае не меняется в рассматриваемом диапазоне и равен θ F ≈ 50 рад/см [24 – 27]). Для гадолиний-галлиевого граната Gd 3 Ga 5 O 12 также можно считать ДП постоянной и равной ε 2 =3,6 [28]. Толщины нанослоёв выбраны следующими: l 1 =400 нм для слоя висмут-замещенного железо-иттриевого граната, l 2 = 100 нм для слоя Gd 3 Ga 5 O 12 .

В качестве полупроводника выбран легированный n-InSb с концентрацией электронов n ≈ 6∙1018 см-3 и значениями нелинейно-оптических восприимчиво-стей 3-го порядка χ1 = χ2=0,01 см3/эрг [29]. Вследствие большого значения кубической восприимчивости у InSb [30] вклад χE2 в ДП оказывается заметным при полях порядка десятков единиц СГСЭ. Нелинейностью 2-го порядка в кристалле InSb можно пренебречь из-за наличия симметрии инверсии.

Известно, что для железо-иттриевого и гадолиний-галлиевого гранатов существует окно прозрачности в диапазоне длин волн Δλ = 1 –6 мкм. Более того, в случае висмут-легированного железо-иттриевого граната этот диапазон может расширяться в длинноволновую область до 8–10 мкм [24, 28, 31]. Оптические потери в полупроводнике также можно считать относительно низкими (порядка 102 см-1) в рассматриваемом диапазоне длин волн [32, 33]. В связи с этим далее мы полагаем потери в системе пренебрежимо малыми.

На рис. 2 изображены дисперсионные зависимости ω(β), рассчитанные в рамках трёх описываемых подходов для значений величины E x (0) =5 и E x (0) = 15 (эрг/см³)^1/2 (рис. 2 а и 2 б соответственно).

Штрихпунктирные линии 1 –4 отвечают решениям ДУ (6) для линейного случая, штриховые линии 1'–2' отвечают решениям ДУ (11) для «одноосного» приближения, сплошные линии 1" –4" соответствуют решениям ДУ (18) для «двуосного» приближения. Все дисперсионные кривые ограничиваются асимптотами A 1 и A 2 , соответствующими объёмным волнам в СМ (при этом ω = c β / ε _⊥ , т.е. q g = 0).

Объёмным волнам в полупроводнике в линейном и «одноосном» приближениях соответствуют асимптоты C 1 и C 2 (для них закон дисперсии следует из решения уравнения q s =0), а в «двуосном» приближении – асимптоты C 1 " и C 2 ", полученные из условия обнуления продольной компоненты электрического поля ПП, т.е. из решения уравнения

• - B +V B ² - 4 AC = 0.

Указанные асимптоты типа « С » ограничивают ветви 3, 4, 3" и 4" в точках пересечения с линиями A 1 и A 2 и имеют нули на частоте

ω _s = ω _p Vε ∞ /( ε ∞ +χ 1 E x ²(0)). (20)

Формула (20) сводится к линейному случаю при χ 1 → 0. Пунктирные линии D 1 и D 2 ограничивают режим распространения солитоноподобных ПП и соответствуют условию обнуления поперечной компоненты волнового вектора в нелинейном полупроводнике:

β

• ² - k ₀ ² ε _x ^N _x ^L = 0 ,

xx s 1 E_x (0) ² + χ ₂ E_z (0) ² . При этом величина E x (0) фиксируется, а поле E z (0) находится как частное решение уравнения (15):

Ez(0) =±V(-B+VB2 -4AC)/2A , где знак «+» соответствует ветви 3", а «–» отвечает ветви 4".

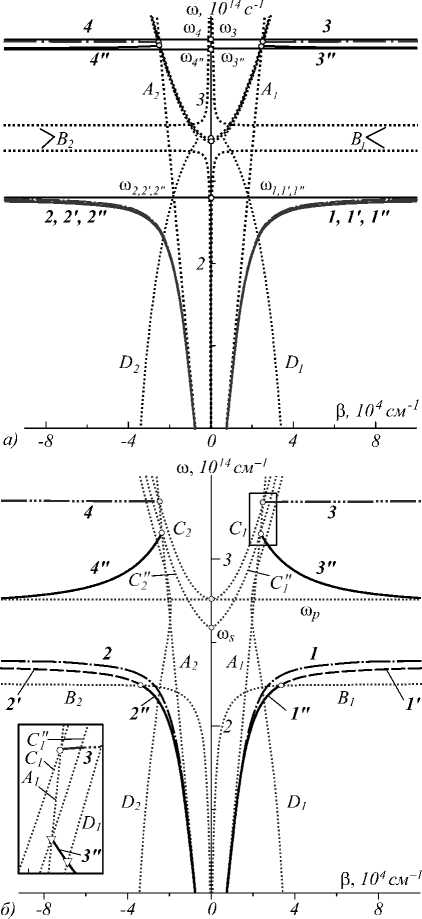
Рис. 2. Дисперсионные зависимости ω(β) для ПП при E x = 5 (а) и 15 (эрг/см³)^1/2 (б). Кривые (1,2,3,4), (1',2') и (1", 2'', 3",4") – отвечают соответственно линейному случаю, «одноосной» и «двуосной» моделям. Асимптоты А 1,2 соответствуют объёмным волнам в СМ, а С 1,2 и С 1,2 " – объёмным ПП в полупроводнике в линейном и «двуосном» приближениях соответственно; линии D 1,2 определяют отсечку солитоноподобных ПП, а B 1 и B 2 – отсечку низкочастотных ветвей в «двуосном» приближении

ДУ (6), (11) и (18) при β → ∞ дают асимптоты ω k ( k = 1, 2, 3, 4), ω l ( l = 1', 2') и ω m ( m = 1", 2", 3", 4"), ограничивают дисперсионные кривые в линейном, «одноосном» и «двуосном» приближениях соответственно.

Как видно на рис. 2, низкочастотные ветви решений ДУ для «одноосного» (1' и 2') и «двуосного» (1" и 2") приближений практически совпадают как при малом значении поля Ex(0) (рис. 2а), так и с его увеличением (рис. 2б), однако во втором случае происходит отсечка ветвей 1" и 2". В дисперсионных спектрах для «одноосного» приближения отсутствуют высокочастотные ветви, т.к. при выводе ДУ в данном подходе накладывается условие εs <0, т.е. действительные решения существуют только при ω < ωp.

При вычислении интеграла (17) необходимо выбрать «физичные» решения, удовлетворяющие условию E x → 0 при x → ∞. Это приводит к появлению асимптот B 1 и B 2 , отвечающих решениям уравнения e NL + 2 % 1 E x (0) = 0 и ограничивающих низкочастотные ветви в «двуосном» приближении. Анализ показывает, что отсечка для ветвей 1" и 2" наступает при значении поля E x (0) > 13,1 (эрг/см³)^1/2.

С ростом E x (0) диапазон существования высокочастотных ПП увеличивается, но ветви 3" и 4" начинают ограничиваться снизу частотой ω p , что обусловлено указанным требованием «физичности» решений. В «одноосном» приближении данное требование выполняется во всём частотном диапазоне существования решений ДУ, а ветви 1' и 2' ограничиваются сверху асимптотическими частотами ω 1 ' и ω 2 ' (на рис. 2 б не показаны).

О невзаимном характере распространения ПП можно судить, исходя из различия между значениями асимптотических частот для дисперсионных кривых с разными по знаку величинами β (ω 1 = 2,3991∙10¹⁴ с^-1, ω 2 = 2,3996∙10¹⁴ с^-1 для E x (0) =5 (эрг/см³)^1/2). Малое (в четвёртом знаке после запятой) различие частот в данном случае вызвано слабой гиротропией и малым значением недиагональных компонент тензора ДП СМ.

На рис. 3 представлены пространственные распределения компонент полей электромагнитной ТМ-волны E x ( x ) (рис. 3 а ), H y ( x ) (рис. 3 б ), E z ( x ) (рис. 3 в ), а также продольной компоненты вектора Умова–Пойн-тинга S z ( x ) (рис. 3 г ), полученные для значения амплитуды поля поверхностной волны в полупроводнике E x (0) = 15 (эрг/см³)^1/2. Плотность потока энергии S z ( x ) (рис. 3 г ) вычисляется по формуле

S z = ( c /8 n )Re( e_xh „ y (21)

В табл. 1 приведены частоты и соответствующие значения констант распространения β, используемые в расчётах, а также значение координаты x 0 .

Табл. 1. Параметры к рис. 3

Номер кривой (приближение)	ω, 1014 с-1	β, 104 см-1	x 0 , 10-4 см
1 (одноосное)	2,0	2,0166	0,387026
2 (двуосное)	2,0	1,9735	0
3 (двуосное)	3,14	–2,4204	0,367874

Разрыв компоненты Ex имеет место для всех случаев, однако для «двуосной» модели имеет место также изменение знака (кривая 2 на рис. 3a). Компонента Sz(x) в этом случае также меняет знак. При этом значение и соответственно знак поля Ex на границе (x = 0+0) фиксированы во всех случаях. Видно, что знаки тангенциальных компонент полей Hy и Ez различаются в «одноосном» и «двуосном» приближении: поле Hy в «одноосном» приближении положительно в обеих средах и отрицательно в «двуосном», в то время как поле Ez в обеих средах в «одноосном» приближении отрицательно и положительно в «двуосном» (кривые 1 и 2 на рис. 3б, в). Амплитуды полей, рассчитанных в «одноосном» при- ближении, примерно в два раза выше амплитуд, рассчитанных в «двуосном» приближении. Для низкочастотных ПП с увеличением координаты поле Ez, например, уменьшается до значений менее 1 (эрг/см3)1/2 при x > 1,82 мкм в «одноосном» приближении (кривая 1) и при x > 0,87 мкм в «двуосном» приближении (кривая 2). Высокочастотные ПП, однако, в «двуосном» приближении затухают более медленно: Ez < 1 (эрг/см3)1/2 при x > 2,13 мкм (линия 3 на рис. 3в). Подобная картина наблюдается и для компонент Ex и Hy, и для потоков Sz.

Отличительной чертой «одноосного» приближения является наличие ярко выраженного пика распределения компоненты Ez (линия 1 на рис.3в), координата которого рассчитывается как x 0 = ArcCosh

1 ¹ f, I,   4 q ; E Xo

I 2 1" V1"

I V

x ' -1/2

/ q_s .

ПП с подобным профилем волнового поля принято называть солитоноподобными [22, 34–37]. Профильные функции H y и E x , в отличие от E z , имеют тангенциальную зависимость от х (см. систему (10)), вследствие чего координата x 0 соответствует положению узла в распределениях этих компонент. Таким образом, точке x 0 в полупроводнике соответствует максимум поля E z , в то время как компоненты H y , E x и S z равны нулю. Компоненты E x и H y с увеличением координаты достигают максимума, затем переходят через ноль и достигают минимума, после чего затухают, а распределение S z в этом случае имеет два максимума (кривая 1 на рис. 3 а , б, г ). В «двуосном» приближении солитоноподобные профили распределения E z ( x ) имеют только высокочастотные ПП (кривая 3 на рис. 3 в ). Область существования солитоноподобных ПП в «двуосном» приближении ограничивается асимптотами A 1,2 и D 1,2 и выделена треугольниками на вставке на рис. 2 б . Координаты максимумов поля E z ( x ) приведены в табл. 1.

Заключение

Проведены теоретические исследования дисперсионных, полевых и энергетических свойств поверхностных ТМ-поляритонов в направляющей структуре на основе полупроводника (n-InSb) и СМ (чередующиеся слои висмут-содержащего феррит-граната и галлийгадолиниевого граната) в среднем ИК-диапазоне (5÷20 мкм). Рассмотрение проведено для линейного случая (скалярная ДП полупроводника) и нелинейных случаев «одноосного» и с физической точки зрения более корректного «двуосного» представления тензора ДП полупроводника. В обеих нелинейных моделях на дисперсионных спектрах найдены частотные области, соответствующие солитоноподобным распределениям компоненты Ez электрического поля ТМ-поляритона. Обнаружено, что рост характерного масштаба нелинейности χE2 приводит к заметной перестройке дисперсионных спектров ω(β). Важнейшим выводом работы является то, что, несмотря на сходные с «двуосной» моделью результаты моделирования дисперсионных спектров нелинейных поляритонов в структуре, часто используемое «одноосное» приближение может стать непригодным для построения полей и потоков электромагнитной энергии в структурах, подобных рассмотренной.

В качестве экспериментального аспекта развития данной тематики можно указать на возможность создания гиротропии в InSb за счет существенного увеличения внешнего магнитного поля. В антимониде

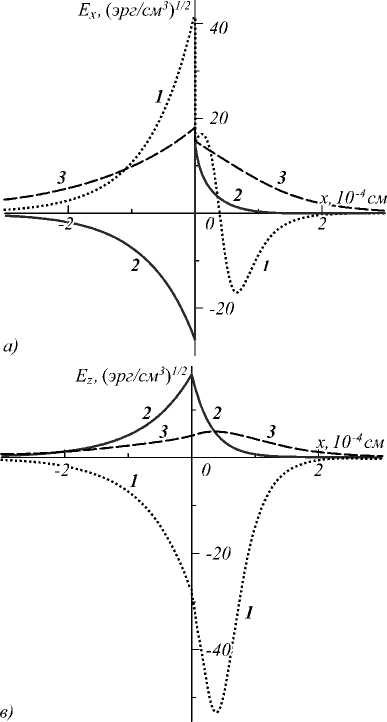
Рис. 3. Распределения компонент поля электромагнитной волны E x (x) (а), H y (x) (б), E z (x) (в) и продольной компоненты вектора Умова–Пойнтинга S z (x) ПП ТМ-типа в «одноосном» и «двуосном» приближениях при E x = 15 (эрг/см³)^1/2.

Нумерация кривых – в соответствии с табл. 1

Работа выполнена при поддержке Министерства образования и науки РФ в рамках государственного задания на НИР (№3.8154.2017/БЧ) и проекта №14.Z50.31.0015.