Спектральный метод голографического помехоустойчивого кодирования

В современных оптических исследованиях ставятся и решаются на основе новых подходов задачи, связанные с регистрацией, обработкой и анализом амплитудных и фазовых характеристик, изменяющихся во времени оптических сигналов произвольной структуры. Одним из методов решения этих задач является введение дополнительной спектральной модуляции [1]. Поскольку речь идет об амплитудной и фазовой информации, решение таких задач для сигналов, изменяющихся во времени, обычно проводится с помощью голографических методов, в том числе с помощью спектральной голографии [2].

В настоящее время применение математических моделей и методов обработки изображений все больше выходит за рамки области обработки собственно изображений. В первую очередь это относится к цифровой голографии и использованию ее принципов, например, для квантовых вы- числений. Практическая реализация квантовых вычислений ограничена рядом проблем, среди которых следует выделить погрешность измерения состояния квантовой системы, нестабильность квантовых состояний вследствие декогерентности. Использование квантовых кодов коррекции ошибок позволяет бороться с декогерентностью, восстанавливая квантовые состояния, уменьшая одновременно погрешность измерений. В [3] высказано предположение, что квантовый код исправления ошибок можно рассматривать как голографическое проявление пространства-времени. Применение голографических кодов для исправления ошибок квантовых компьютеров рассмотрено в работах [4–7]. В 2019 г. Министерство обороны США выделило финансирование на исследования голографических кодов исправления ошибок для квантовых компьютеров [8].

Другим примером расширения сферы применения голографических принципов является помехоустойчивое кодирование. В [9–11] рассмотрено использование голографического кодирования произвольной цифровой информации для повышения помехоустойчивости каналов связи и надежности передачи информации.

Дальнейшим расширением области применения голографических методов обработки информации является переход в спектральную область, спектральная голография. Непосредственная обработка спектра сигнала и пространственного спектра изображения представляет интерес и для задач фильтрации, модуляции и кодирования.

Спектральная модуляция применима, например, в беспроводных системах передачи информации, использующих сверхширокополосные шумоподобные сигналы. Это дает высокую помехоустойчивость, электромагнитную совместимость и способность передавать информационые сообщения “глубоко под шумами” в каналах связи с сильными помехами [12].

Спектральное кодирование

Объединение двух методов – голографического кодирования и непосредственной обработки спектра сигнала в метод спектрального голографического кодирования – дает еще более высокий результат в повышении помехоустойчивости систем передачи информации.

В [13] показана возможность кодовой спектральной модуляции потока двоичных информационных символов и когерентного сжатия широкополосных шумоподобных сигналов в приемнике в результате двойной спектральной обработки с последующим восстановлением передаваемой информации.

В системах цифровой радиосвязи, например в GSM, широко применяется модуляция GMSK (Gaussian Minimum Shift Keying) – гауссовская двухпозиционная частотная манипуляция с минимальным сдвигом. Для GMSK обычно используют одну из двух схем модуляции – с управляемым по частоте генератором или квадратурным модулятором. Модуляторы/демодуляторы могут быть как аналоговыми, так и цифровыми, но в любом случае в них существуют переходные процессы, связанные с установлением частоты, а также групповые задержки фильтров, огранивающие минимальную длительность пачки импульсов.

При спектральном голографическом кодировании с дискретной частотной манипуляцией процесс кодирования заключается в формировании N радиоимпульсов на ортогональных частотах (набор частот определен голографическим кодером для каждой посылки) путем коммутации (манипуляции) выходов N генераторов гармонических сигналов, работающих в постоянном режиме. Поэтому переходные процессы, связанные с изменением частоты, отсутствуют, как отсутствуют и фильтры любого вида. Формирование группового сигнала происходит суммированием манипулированных гармоник на входе усилителя передатчика или прямо в антенне.

При декодировании необходимо провести обнаружение в принятом сигнале каждой из N используемых частот. В аналоговой технике для этого нужно N избирательных фильтров с очень узкой полосой пропускания. При цифровой обработке необходимо оцифровать принятый сигнал (без фильтрации), выполнить дискретное преобразование Фурье и определить в принятой посылке наличие или отсутствие каждой из N частот. Полученная двоичная последовательность (1 – наличие гармоники, 0 – отсутствие), представляющая собой спектр сигнала, подвергается голографическому декодированию, и из нее извлекается переданное двоичное слово.

Спектральное голографическое кодирование с дискретной частотной манипуляцией обеспечивает выигрыш в помехоустойчивости за счет совместного действия трех механизмов: частотная манипуляция, спектральное кодирование и голографическое кодирование.

В [11] описано голографическое помехоустойчивое кодирование, применяемое к сигналу, подлежащему передаче по цифровому каналу связи. Двоичный k -разрядный блок исходных данных заменяется N -разрядным ( N = 2 ^k ) кодовым словом, представляющим собой линейную одномерную голограмму виртуального точечного источника, позиция которого в пространстве определяется значением кодируемого блока.

Однако в силу дуальности представления сигналов аналогичные преобразования возможны и в частотной области, применимо к спектру сигнала. В зависимости от условий передачи и характеристик канала связи это может дать выигрыш в помехоустойчивости. Одним из таких способов является спектральное голографическое кодирование.

В отличие от описанного в [11] метода кодирования изменяющегося во времени сигнала путем замены его формы формой его виртуальной голограммы, при спектральном голографическом кодировании создается сигнал с заданным спектром. Форма спектра при этом является той же одномерной голограммой, значения которой округлены до одного бита, и представляет собой двоичную последовательность.

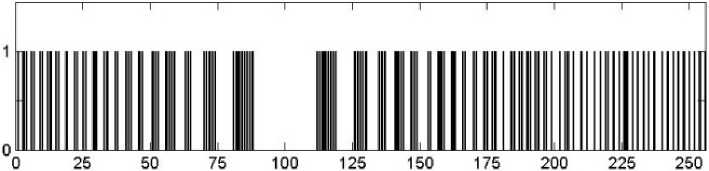
Рисунок 1. Форма спектра – линейная голограмма (последовательность нулей и единиц) длиной N = 256

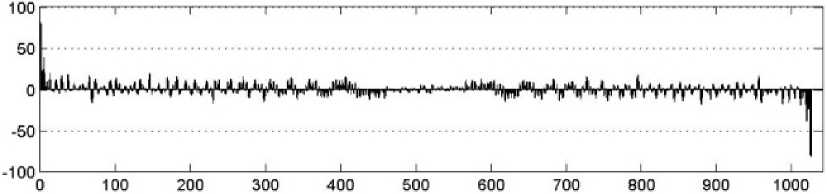
Рисунок 2. Сигнал, образованный суммой синфазных гармоник

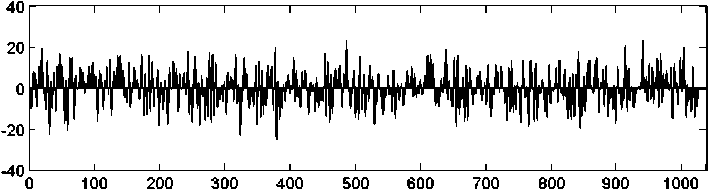
Рисунок 3. Сигнал, образованный суммой гармоник со случайной фазой

Кодируемое значение блока – это номер позиции центра голограммы (центра зон Френеля) в кодовом слове, в данном случае X = 100 (рисунок 1).

Для создания сигнала со спектром такой формы достаточно сложить набор гармоник равной амплитуды с номерами, соответствующими номерам позиций единиц в голограмме. Гармоники с номерами, соответствующими позициям нулей, в образовании сигнала не участвуют. Эта операция является дискретной частотной манипуляцией N гармониками.

Вопросы минимизации погрешности передачи информации с помощью многоимпульсной позиционно-импульсной модуляции по лазерным каналам связи рассмотрены в [16]. Этот способ модуляции имеет общие черты с голографическим кодированием, так как в обоих случаях используется позиционное кодирование.

Если все гармоники имеют одинаковую начальную фазу, суммарный сигнал содержит большой выброс в начале и конце (рисунок 2), что нежелательно из энергетических соображений. Поэтому фазы гармоник должны быть распределены, например, по случайному закону. Сигнал в этом случае имеет шумоподобную форму (рисунок 3).

Важным требованием является необходимость того, что длительность сигнала (кодового слова) должна быть равна целому числу периодов всех используемых гармоник (в данном примере – один период низшей гармоники и 256 периодов высшей). В этом случае спектр сигнала является дискретным (линейчатым) и строго соответствует рисунку 1.

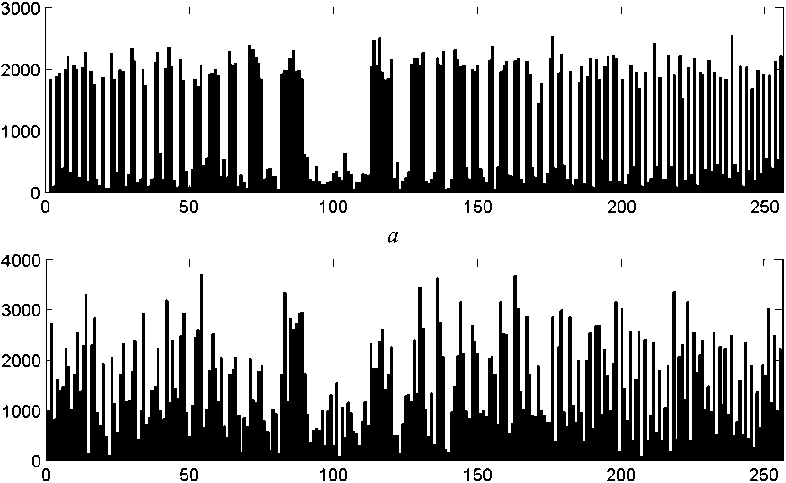
При наложении на сигнал аддитивного белого шума спектр сигнала также искажается (рисунок 4).

Результаты моделирования

Исследование спектрального голографического кода проведено путем моделирования в среде MATLAB процесса кодирования и передачи информации в присутствии белого гауссовского шума.

Декодирование сигнала в приемнике производилось путем вычисления спектра принятого сигнала, а к нему применялось обратное голографическое преобразование, которое восстанавливает номер позиции центра голограммы – значение исходного блока данных (рисунок 5).

Ключевым фактором, определяющим помехоустойчивость рассматриваемого метода, является относительная длительность суммарного гармо-

б

Рисунок 4. Спектр сигнала на входе приемника при отношении сигнал/шум +5 дБ ( а ) и –5 дБ ( б )

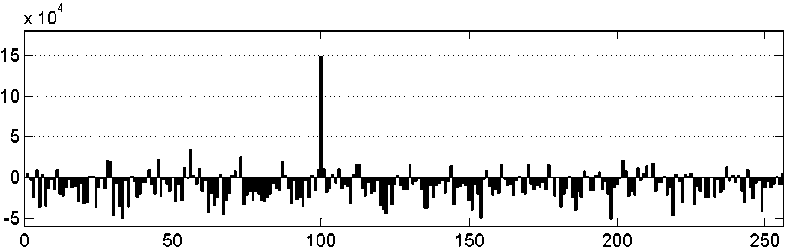
Рисунок 5. Результат восстановления голограммы при отношении сигнал/шум –10 дБ

б

а

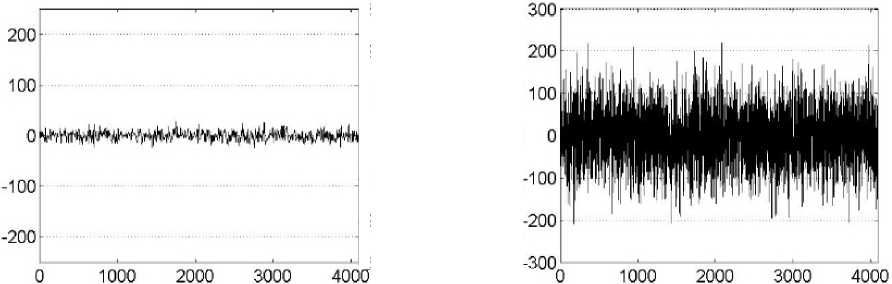
Рисунок 6. Сигнал ( а ) и шум ( б ) при отношении сигнал/шум –18 дБ

нического сигнала. В рассматриваемом примере частота высшей гармоники в 16 раз меньше частоты дискретизации сигнала в приемнике. При этом вероятность ошибки декодирования составляет 0,01 при отношении сигнал/шум –18 дБ. На рисунке 6 приведены графики сигнала и шума в одном масштабе для этого случая.

Увеличение количества отсчетов в периоде высшей гармоники (увеличение частоты дискретизации) увеличивает выигрыш в помехоустойчивости.

Для оценки помехоустойчивости спектрального голографического кодирования проведено сравнительное моделирование процесса переда-

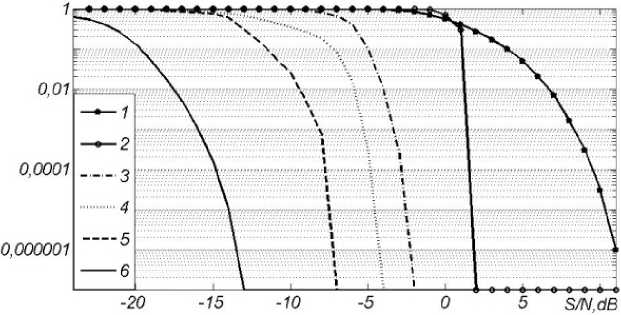
Рисунок 7. Зависимость вероятности ошибки декодирования P o от отношения сигнал/ шум при скорости кода R = 1/32: 1 - без кодирования; 2 - РС-код; 3 - РМ-код;

4 – мажоритарный код; 5 – голографический код; 6 – спектральный код

чи информации по каналу с аддитивным белым гауссовским шумом при использовании широко применяемых кодов. Рассмотрена зависимость вероятности ошибки декодирования от отношения сигнал/шум в канале для кода Рида – Соломона (РС-кода), кода Рида – Маллера (РМ-кода), мажоритарного кода, голографического и спектрального кода. Для этого к результатам, полученным в [11], добавлены результаты моделирования работы спектрального кода. Во всех случаях число разрядов исходного слова – 8, длина кодового слова – 256 бит (скорость кодов R = 1/32). Результаты приведены на рисунке 7. Из графиков видно, что спектральное голографическое кодирование обеспечивает выигрыш в помехоустойчивости на 7–8 дБ по сравнению с кодированием непосредственно сигнала.

Другим преимуществом спектрального кода являются меньшая сложность кодирования и декодирования при изменении избыточности в широких пределах, а также высокая скрытность в связи с использованием шумоподобного сигнала.

Заключение

Спектральный голографический код представляет интерес для передачи информации по каналам с низким уровнем сигнала, например, при передаче изображений по каналам дальней космической связи, когда задача принимать слабый сигнал на уровне тепловых шумов приемника имеет более высокий приоритет, чем скорость передачи.

Исследование выполнено за счет гранта Российского научного фонда № 22-29-00041,