Спектры отражения и прохождения одномерного фотонного кристалла с дефектом из монослоя наночастиц

Использование в качестве материалов, составляющих ФК, сред с управляемыми свойствами открывает широкие возможности для создания модуляторов, оптических изоляторов, преобразователей поляризации света. Особый интерес вызывают слоисто-периодические структуры на основе сред, имеющих резонансную частотную зависимость магнитной и (или) диэлектрической проницаемостей, в том числе плазмонных нанокомпозитов. Нанокомпозиты (НК) могут состоять из изотропных и анизотропных материалов, включая диэлектрики, металлы, полупроводники, сегнетоэлектрики и ферромагнетики. Свойства нанокомопозита могут значительно отличаться от свойств образующих его материалов. Этими свойствами можно управлять, варьируя внутренние геометрические параметры (размер и форму включений), а также с помощью внешних полей. Так, характеристики ФК структур на основе активных диэлектрических материаллов существенно зависят от величины внешнего электрического поля. Его направление существенно не только по отношению к направлению распространения волны, но и к направлению оси периодичности структуры. Дисперсионные свойства такой структуры во многом определяются частотной и полевой зависимостью диэлектрической проницаемости компонент структуры, наличием диссипации или усиления [1-5].

Одной из современных задач является изучение эффектов в одномерных ФК, содержащих слои нанокомпозита (НК) [6-8]. В работе [8] про

веден анализ спектров отражения и пропускания одномерного ФК с дефектным слоем, выполненным в виде однородного матричного нанокомпозита с металлическими наночастицами несферической формы, и продемострирована возможность управления дефектными модами за счет варьирования формой наночастиц. В настоящей работе исследуется особенности спектров отражения и прохождения “дефектного” ФК, дефектный слой которого представляет собой нанокомпозит с монослоем металлических наночастиц, плоскость которого ориетирована перпендикулярно оси периодияности ФК.

1. КОЭФФИЦИЕНТЫ ОТРАЖЕНИЯ И ПРОПУСКАНИЯ ФК

Для расчета отражательной и пропускной способностей одномерной плоско-слоистой структуры с внедренным монослоем наночастиц воспользуемся матричным методом для интерфейсов. Под интерфейсом понимается геометрическое место точек (плоскости в рассматриваемом случае), на котором происходит разделение падающей волны на преломленную и отраженную. Частным случаем интерфейса является граница раздела двух сред. Оптические хараткерис-тки такого интерфейса определяются френелевскими коэффициентами отражения и пропускания [9]. Поскольку монослой наночастиц, то есть массив наноразмерных частиц, расположенных в одной плоскости, взаимодействует с электромагнитной волной подобно плоской границе раздела двух сред, то есть создает отраженную и преломленную волны, а их углы отражения и преломления подчиняются закону Снел-лиуса, он также может рассматриваться как интерфейс с некоторыми собственными коэффициентами отражения и пропускания.

Пусть в слоистой среде имеется N интерфейсов, образрванных N -1 границами раздела сред и одним монослоем наночастиц. Пространство между интерфейсами заполнено средами с различными показателями преломления n i ( z = 0... N ) . Среды с показателями преломления n ₀ и n N являются полубесконечными. Пусть на слоистую среду в направлении оси z падает плоская монохроматическая волна. Для описания ее распространения в ФК введем следующие обозначения: E i ( z. ) - напряженность поля слева от интерфейса c номером i , E i ( z . ) - напряженность поля справа от интерфейса c номером i , E f - напряженность поля волны, распространяющейся “вперед”, E b - напряженность поля волны, распространяющейся “назад”, to и к = to / с - частота и волновое число.

Согласно введенным обозначениям на интерфейсе с номером m в слое с показателем преломления n m _{- 1} напряженности полей распространяющихся навстречу друг другу волн равны ^Ef ⁽ z m ) и E b ( z m ) . На том же интерфейсе, но в слое с показателем преломления n m они равны ^Ef ⁽ z m ) и E b ( z . ) . Взаимосвязь этих полей на m -ом интерфейсе (слева и справа от него) может быть выражена в виде матричного уравнения:

слева от первого интерфейса и справа от после-

днего интерфейса с номером N :

fE, (z;)) _ g. fE, (zN) ^ V E„ (z-) J V E„ (zN) J

G = I FI F I

^{VJ 1} 0,1-*- 1¹1,2-*- 2 NN-1¹ N - 1, N .         ⁽⁶⁾

Заметим, что в среде N с показателем преломления n N существует только прошедшая волна, поэтому в (5) следует положить E b ( z N ) = 0 .

Отражательная и пропускная способности всей структуры расчитывается по формулам

^G 11

G

^G 11

2. СПЕКТРЫ ОТРАЖЕНИЯ МОНОСЛОЯ НАНОЧАСТИЦ

¹ m - 1, m

fE,(z;))_I _ fE, (zm))

—f1

r m-1, m V m-1, m

m , m - 1

tt m-1, m m, m-1

r r ,(2)

* m - 1, m'm , m - 1 J

Г j , t, j - амплитудные коэффициенты отражения и пропускания интерфейса, разделяющего среды с показателями преломления n i и n j , при падении световой волны со стороны среды с показателем преломения n i . В случае плоской границы раздела сред коэффициенты r i _, j и t i _, j есть френелевские амплитудные коэффициенты отражения и пропускания [9].

Взаимосвязь полей на двух интерфейсах с номерами m и m + 1 , ограничивающих однородный слой с номером m , осуществляется передаточной матрицей одного слоя F m :

f m f f m E, (z-) J    m [E, (z+).

bm     bm

Для анализа свойств ФК с нанокомпозитным дефектом в виде монослоя наночастиц, помещенного в диэлектрическую матрицу, необходимо знать амплитудные коэффициенты отражения и преломления монослоя. Аналитический расчет этих коэффициентов является нетривиальной задачей, поэтому в настоящей работе применен численный метод – метод конечных элементов, реализованный в пакете программ физического моделирования COMSOL Multiphysics.

Выберем в качестве объекта моделирования монослой металлических наночастиц вытянутой эллипсоидальной формы с аспектным отношением 1:2, помещенный в диэлектрическую среду с проницаемостью £ _m . Пренебрегая поглощением и частотной дисперсией диэлектрика, используемого в качестве матрицы композита, положим параметр £ постоянной действительной величиной равной 2.25. Для расчета диэлектрической проницаемости металлических наночастиц воспользуемся соотношением теории Друде[9]:

£p (to) _ £0

to2

2 . ■           ’

to + ztoy

где 3 _m _ kn_md_m - фазовая толщина слоя.

Применяя выражения (1) - (4) ко всей слоисто-периодической структуре, получим связь поля

F

m

где to p - плазмонная частота; £ ₀ - вклад решетки; У - параметр релаксации. Для определенности при численном анализе в качестве материала наночастиц будем использовать серебро, для которого to _p =1.36 ■ 10¹⁶ c - 1 , е ₀ =5 , У = 3 - 10¹³ С - 1 [9]. Рассмотрим случай, когда оси металлических наночастиц одинаково ориентированы вдоль некоторого направления в плоскости монослоя.

Результаты моделирования оптических свойств монослоя серебряных наночастиц представлены на рис. 1. Видно, что спектры действи-

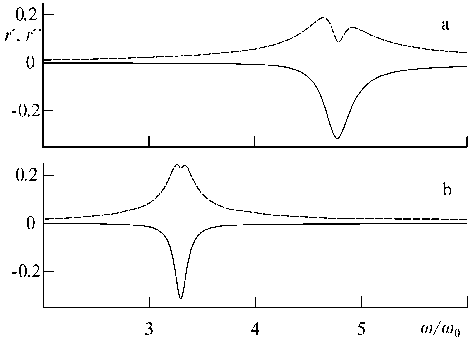
Рис. 1. Действительная и мнимая части (сплошная и пунктир) коэффициента отражения монослоя наночастиц для случаев тангенциальной (a) и продольной (b) ориентации светового вектора. Наночастицы образуют на плоскости квадратную сетку с периодом 140 нм тельной и мнимой частей аплитудного коэффициента отражения рассматриваемой среды зависят от ориентации осей эллипсоида относительно направления ориентации светового вектора в электромагнитной волне. Наблюдается сдвиг резонасных частот для случаев тангенциальной и поперечной ориентаций осей эллипсоидов относительно направления вектора напряженности электрического поля световой волны. Этот сдвиг обусловлен отличием частот поверхностных плазмонных резонанснов наночастиц эллипсоидальной формы: одна из этих частот отвечает колебаниям электронов металла в направлени полярной оси наночастицы, а другая – в перпендикулярном направлении.

Анализ также показывает, что амплитудный коэффициент отражения существенно зависит и от концентрации наночастиц в монослое. С уменьшением расстояния между наночастицами, то есть при увеличеннии их поверхностной концентрации в монослое, резонансы коэффициента отражения становятся более выраженными, их ширина увеличивается, резонасные частоты смещаются. Таким образом, спектральные характеристики монослоя металлических наночастиц существенно зависят от внутренних геометрических параметров, что позволяет настраивать их резонансы на эффективное взаимодействие со светом в заданном спектральном интервале.

• 3    АНАЛИЗ СВОЙСТВ ДЕФЕКТНОГО ФОТОННОГО КРИСТАЛЛА

С МОНОСЛОЕМ НАНОЧАСТИЦ

Рассмотрим ФК, в котором между двумя диэлектрическими ФК зеркалами, инвертированными относительно друг друга, включен дефект- ный слой, состоящий из рассмотренной выше диэлектрической матрицы и монослоя наночастиц. Передаточная матрица такой структуры может быть представлена в следующем виде:

N = I o,i F . - I d - 1, d F d i F s F d 2 I d , d ₊ i - F n -i I n -i n = ^V , (9) где F s – передаточная матрица монослоя наночастиц, F d . и F_{d 2} - передаточные матрицы слоев, обрамляющих монослой наночастиц, M a и M b – передаточные матрицы, описывающие ФК зеркала, a и b – число периодов в боковых ФК зеркалах. Период ФК зеркала состоит из двух слоев изотропных диэлектриков с вещественными проницаемостями Е j и толщинами L j ( j = 1, 2). Для моделирования оптических свойств структуры выбираем значения е . = 5.52 ( TiO ₂ ) и Е ₂ = 2.25 ( SiO ₂ ) [11]. Толщина слоев структуры подбиралась равной L . ₂ = Д /4 П . ₂ , толщина дефектного слоя равна L d = ^ /2 n d , где Х ₀ -длина волны в вакууме, рассчитанная для центральной частоты запрещенной зоны. Наличие в ФК дефектного слоя приводит к появлению в фотонной запрещенной зоне узкой спектральной области пропускания с пиковым значением показателя прохождения близким к единице. Дефектная мода пропускания ФК может быть подавлена в случае, когда в нем имеются металлические наночастицы с плазмонным резонансом, лежащим в том же спектральном интервале [7]. Рассмотрим, какое влияние оказывает монослой наночастиц на оптические спектры пропускания и отражения ФК.

На рис. 2 продемонстрировано изменение спектров пропускания и отражения ТЕ моды в структуре м ⁵ dm ⁵ , в которую добавлен монослой плазмонных наночастиц. Для расчета места расположения монослоя наночастиц в области дефекта использовались следующие соотно^шения: L d . = yL_d , L d 2 = L d ^- L d . , 0 <  y <  1 , где L d – толщина дефектного слоя, который монослой наночастиц разбивает на две области толщинами L d . и L d ₂ соответсвенно (область толщиной L d . расположена со стороны падения внешней ЭМВ). Считаем, что размер наночастиц много меньше толщины дефектного слоя. Видно, что при смещении монослоя к краям дефектного слоя, т.е. при значениях у = 0.05 ^ 0.4 и 0.6 - 0.95 , происходит полное подавление дефектной моды (а). При небольших смещениях от центра дефектного слоя подавление дефектной моды становится неполным (b, c), а при нахождении монослоя в центре дефектного слоя подавление вообще отсутствует (d).

На рис. 3. продемонстрировано изменение спектров пропускания и отражения в зависимости от положения монослоя в структуре м ⁵ dm ⁵ , которая отличается от структуры м ⁵ DM ⁵ пере-

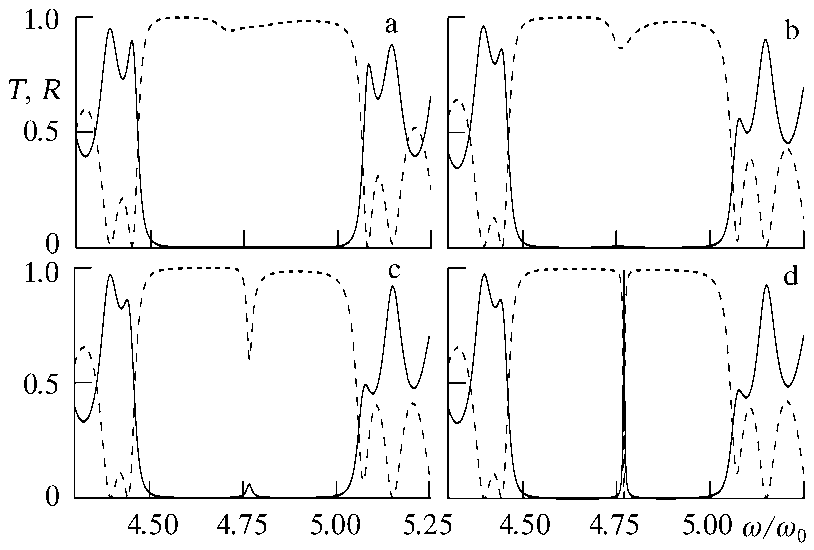
Рис. 2. Спектры пропускания и отражения (сплошная и пунктир) ТЕ моды в зависимости от положения монослоя наночастиц в структуре M ⁵ D M ⁵ . Оси наночастиц направлены перпендикулярно плоскости поляризации волны

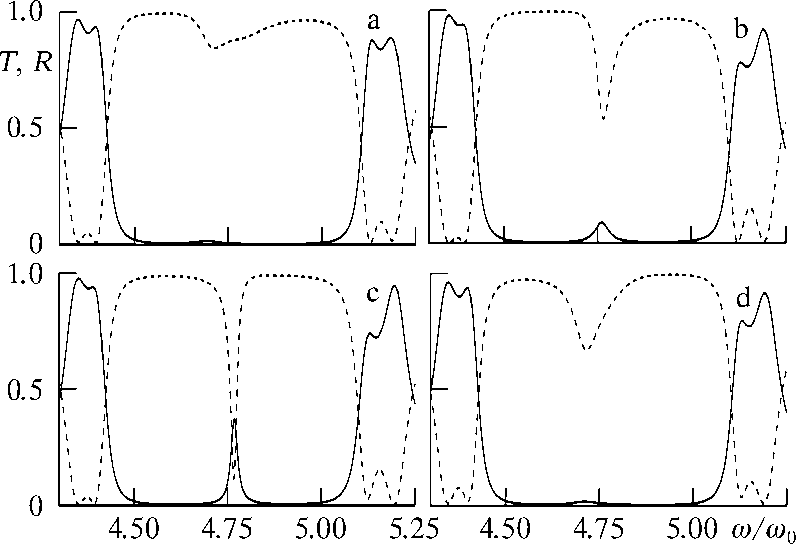
Рис. 3. Спектры пропускания и отражения (сплошная и пунктир) структуры M ⁵ DM ⁵

ставленными зеркалами (остальные параметры те же, что и на рис. 2). В данном случае полное подавление дефектной моды наблюдается при нахождении монослоя вблизи границ раздела дефектного слоя у = 0.05 ^ 0.25 , 0.8 ^ 0.95 и в его центральной области у = 0.4 — 0.6 (случай а). При смещении монослоя от центра дефекта, т.е. при значениях у = 0.25 ^ 0.4 и 0.6 ^ 0.8 (случай b, d), подавление неполное. Максимум пропускания наблюдается при y = 0.65 (случай d).

ЗАКЛЮЧЕНИЕ

Установлена возможность управления коэффициентами пропускания и отражения, отвечающих дефектной моде в фотонной запрещенной зоне, за счет использования монослоя металлических наночастиц. Показано, что амплитуда дефектной моды существенным образом зависит от местоположения монослоя наночастиц. В зависимости от используемой конфигурации ФК

(последовательности слоев в ФК-зеркалах) дефектная мода может подавляется, когда монослой располагается ближе к краям или, наоборот, к середине дефектного слоя. Зависимость спектральных характеристик дефектных ФК от местоположения плазмонного монослоя обусловлена двумя причинами. Первая из них – разный характер распределения поля по дефектному слою в структурах M ⁵ DM ⁵ и M ⁵ DM ⁵ , что приводит к зависимости от фактора y эффективности взаимодействия ЭМВ с наночастицами монослоя и, как следствие, степени его влияния на спектральные характеристики всего ФК. Вторая причина связана с тем, что наличие монослоя наночастиц приводит к дополнительным интерференционным эффектам внутри дефектного слоя, в результате которых пропускание и отражение дефектного слоя существенно изменяются.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследова- ний и Федеральной целевой программы “Научные и научно-педагогические кадры инновационной России на 2009-2013 годы” Министерства образования и науки РФ.