Спиновые и зарядовые корреляции электронов в димере с вырожденными орбиталями и заполнением электронов n = 1,5

Интенсивное развитие нанотехнологий позволяет создавать кластеры произвольной формы и различных размеров [1; 2]. Однако у кластеров, расположенных на границе раздела двух материалов с разным химическим потенциалом, возникает разность потенциалов, под действием которой могут изменяться их спиновые и электронные корреляции.

Особый интерес представляют ионы с орбитальным вырождением и электронной оболочкой, заполненной более чем наполовину. Здесь принципиальную роль играет учет кулоновского взаимодействия между электронами на разных орбиталях [3]. У полупроводников с сильными электронными корреляциями в некоторых случаях это может привести к определенному типу орбитального упорядочения [4]. Для слабовзаимодействующих электронов кулоновское взаимодействие будет способствовать перераспределению спектрального веса в плотности электронных состояний. При напылении пленок разного состава на границе интерфейса возникает контактная разность потенциалов, которая может изменить зарядовое и спиновое упорядочение вблизи поверхности. Если постоянные решетки двух пленок существенно отличаются, то возникающие искажения кристаллической решетки вызовут изменение локальной симметрии и гибридизацию волновых функций электронов, расположенных на разных орбиталях.

Необходимо исследовать влияние контактной разности потенциалов и межорбитальных интегралов перескока, возникающих в результате изменения симметрии кристаллического окружения в димере с вырожденными орбиталями и числом заполнения n = 1,5 в двух предельных случаях: когда кулоновское отталкивание на узле сравнимо с шириной зоны ( U ~ W) и когда кулоновское взаимодействие значительно меньше этой ширины ( U <  W).

Рассмотрим двухузельный кластер с двумя орбиталями на узле и шестью электронами с числом заполнения n = 1,5. Соответствующий гамильтониан в модели Хаббарда [5] имеет вид

H = H1 + H3 + H4 + H5 + H6 + H7 + H8, где

H1 = -Е (е1,а+5) ^.а—Е (е2,а-5) n 2,а,

αα здесь а - номер орбитали, а = 1, 2, 0 < nia = \аЛ + \аЛ’ 0 - nia> 2

нз =-Е ЕЕ ti:1 (cL, cj^+нс);(2)

• i , j а=1 о

H =-ЕЕЕ jCj ,а,о+ НС);(3)

(i , j а=2 о

H5 = — Е ЕЕ tu (cLa c^ + НС),(4)

ii,jа,в о в (2)-(4) i f j, в (4) а f в;

H6 = Е. Е, Е. Ui,а,-аni,а,оni,а,-о ;

• ²    i а о

н7 =1 ЕЕЕ Viooni^onh^;(6)

• ²    i а,в о,o'

• ^H 8 = - Е Е Е Ji ,в ^{( C} Zа,o c i ,а,о‘ ^ До' c i ,в,о ⁺

i а^в о,о'

• ⁺ c i ,а,о c i ,в,о c i ,а,о‘ c i ,в,о' ^{+ НС)}.

0.10 0.05 0.00

В (1)-(7) приняты следующие обозначения: е ± 5 -уровень энергии первого и второго ионов, t _а в - матричный элемент перескока между ближайшими узлами и орбиталями (а,Р); U , V - кулоновское отталкивание электронов на узле и на одной орбитали и между орбиталями соответственно; J - хундовское обменное взаимодействие между электронами на разных орбиталях; c ^L i р ( c i , _о) - операторы рождения (уничтожения) электронов со спином о на узле i ; n i , _о = c ^L i , _о c i , _о.

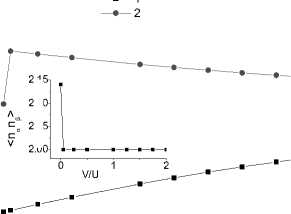
С помощью метода точной диагонализации был вычислен спектр собственных значений, на основе которых определялась величина спин-спиновых корреляционных функций по продольным < S ^z 1 S ^z ₂>, S^z = ( n t ,o — n t ,-о )/2 и поперечным < S ⁺1 S ^-₂>, S⁺ i = c ^L i, _T c^ , S ^- i = c ^L i, I c ii компонентам спина, а также корреляторы электронной плотности между орбиталями < n _а n в > (рис. 1).

Анализ полученных зависимостей спин-спиновых корреляций между узлами от величины кулоновского взаимодействия между орбиталями показывает следующее. При малых параметрах междуорбитального взаимодействия V < V c наблюдается антиферромагнитное расположение спинов. Для двухорбитальной модели с числом заполнения n = 1,5 максимально возможное значение спинового коррелятора < S z 1 S^z ₂> = = -0,125. Зарядовые флуктуации между узлами, например n 1 = 4 и n ₂ = 1, и орбиталями приводят к уменьшению спиновых корреляций электронов на соседних узлах. Уменьшение междуорбитальных электронных корреляций < n _а n в > при V c связано с появлением ферромагнитных спиновых корреляций по поперечным компонентам спина.

-0.05

-0.10

-0.15

2.15

2.10

2.05

0.0        0.5        1.0        1.5        2.0

V/U

Рис. 1. Спин-спиновые корреляционные функции по продольным < S z 1 S z ₂ > ( 1 ) и поперечным < S ⁺ 1 S “₂> ( 2 ) компонентам спина и корреляторы электронной плотности между орбиталями < n _а n р > от величины междуорбитального кулоновского взаимодействия для U / t = 0,2, J / t = 0,5, t ¹² = 0, е 1 - £ ₂ = 0 (вставка)

тронов по орбиталям, например n _а = 1, n в = 2. В результате коррелятор электронной плотности < n _а n в > = 2, а переход электрона с орбитали с n в = 2 на орбиталь с n _а = 1 возможен только при параллельной спиновой конфигурации электронов, что вызывает существенное уменьшение антиферромагнитных корреляций.

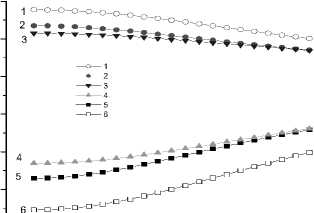
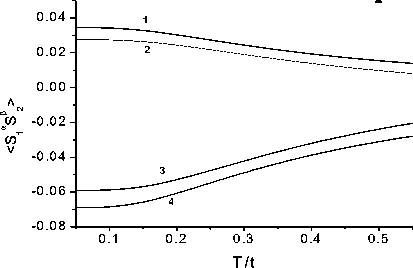
На границе раздела двух материалов разность потенциалов может достигать нескольких электронвольт, что может существенно изменить разность уровней энергии одноэлектронных состояний и вызвать изменение обменного взаимодействия. В частности, параметр обмена J ~ t ²/( U + £ 1 - £₂) [6] во втором порядке теории возмущения уменьшается как с ростом величины зарядовой щели, так и при увеличении кулоновского взаимодействия (рис. 2). При изменении этого параметра от U / t = 0,2 до U / t = 1 наблюдается плавное уменьшение спиновых корреляций как от зарядовой щели, так и от величины кулоновского взаимодействия. Корреляционная функция электронной плотности не меняется и остается постоянной: < n _а n в > = 2. Температурные флуктуации вызывают плавное уменьшение спиновых корреляций без изменения знака.

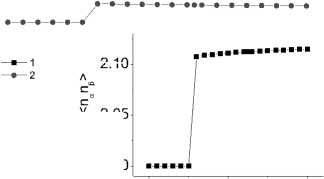
Влияние несогласованности параметров решетки, кристаллических структур, приводящее к упругим искажениям, моделируется дополнительным интегралом перескока между орбиталями (рис. 3). Следует отметить, что при некотором критическом параметре 1 ₁₂ наблюдается резкий рост спиновых и зарядовых корреляций.

Таким образом, межорбитальное кулоновское взаимодействие в димере с вырожденными орбиталями для числа заполнения n = 1,5 приводит к неколлинеарному расположению спинов. Авторами определена зависимость спин-спиновых корреляций между ближайшими узлами от величины зарядовой щели и температуры для U <  t , а также найдено изменение спиновых и зарядовых корреляций электронов на разных орбиталях от величины межорбитального перескока электронов при учете кулоновского взаимодействия между электронами.

-0.12

0.06

0.03

0.00

-0.03

-0.06

-0.09

0.0 0.2 0.4 0.6 0.8     1.0

( ε ₁- ε ₂)/t

б

Рис. 2. Спин-спиновые корреляционные функции по продольным <  S z _t S z ₂ > ( 3 , 4 ) и по поперечным < S + S ~₂ > ( 1 , 2 ) компонентам спина от величины зарядовой щели для U / 1 = 0,2, V ' U = 0, J / t = 0,5 ( 1 , 6 ), J / 1 = 1 ( 2 , 5 ), J / 1 = 1, V / U = 0,3 ( 3 , 4 ) ( а ) и от температуры ( б ) для U / t = 0,2, J / t = 0,5, t ¹² = 0, £ 1 - £ ₂ = 0 ( 1 , 4 ), (£ 1 - £ ₂ )/ t = 0,5 ( 2 , 3 )

0.04

0.00

U) -0.04

<л" ^v -0.08

2.10

2.05

2.00

0.0

0.5

1.0

^t αβ ^/t αα

-0.12

0.0 0.2 0.4 0.6 0.8 1.0

αβ αα

Рис. 3. Спин-спиновые корреляционные функции по продольным < S z 1 S z 2 > ( 1 ) и по поперечным < S +1 S –2 > ( 2 ) компонентам спина и корреляторы электронной плотности между орбиталями < n _α n β > от величины интеграла перескока между разными орбиталями для U / t = 0,2, J / t = 0,5, ε 1 – ε 2 = 0 (вставка)