Спиновый эффект Холла при прохождении света с линейной поляризацией через метаповерхность

Разделение левой и правой эллиптических поляризаций с помощью метаповерхности впервые было реализовано в [1]. В этой работе изучали прохождение света ближнего ИК-диапазона (1,2 – 1,7 мкм) через метаповерхность, состоящую из периодических золотых наноантенн V-формы. В дальнем поле измерялась третья компонента вектора Стокса. Было показано, что в световом пучке сформировались две области на краях пучка с компонентой Стокса разного знака. То есть в пучке присутствуют области с левой и правой эллиптическими поляризациями. В [2, 3] с помощью металинзы усиливали поперечное смещение пучков с левой и правой круговыми поляризациями. Например, в [3] для усиления эффекта Холла использовали субволновую дифракционную решетку. Но смещение пучков с разным спином происходило вдоль штрихов решетки. В [4] для длины волны 633 нм и с помощью q-пластинки получили расщепление вихревого пучка с линейной поляризацией на Гауссов пучок с левой круговой поляризацией и вихревой пучок с правой круговой поляризацией. В работах [5– 10] исследовались поляризационные конверторы на основе метаповерхностей для волн миллиметрового диапазона. Например, в [7] метаповерхность из металлических полосок освещается миллиметровым излучением с линейной поляризацией и под углами 30 градусов отражаются два пучка с левой и правой круговой поляризацией. А в [8] рассчитана отражающая

метаповерхность для миллиметрового диапазона для преобразования пучка с линейной поляризацией в два пучка с левой и два с правой круговой поляризацией. Аналогичная метаповерхность, но для демонстрации спинового эффекта Холла на пропускание рассматривается в [9]. В работах [11, 12] рассматриваются метаповерхности для преобразования поляризации для инфракрасного излучения, а в [13– 15] для видимого диапазона. Заметим, что в перечисленных работах теоретически не исследовалось распространение света после металинз.

С другой стороны, для понимания спинового эффекта Холла можно рассматривать, как он проявляется при распространении некоторых векторных пучков. Разделение левой и правой круговой поляризации в остром фокусе было показано для некоторых типов векторных пучков в [16, 17] и даже при распространении параксиальных векторных пучков [18, 19]. При этом в начальной плоскости у таких пучков была однородная или неоднородная линейная поляризация. Например, в [20] показано, что в остром фокусе оптического вихря с линейной поляризацией имеет место спиновый эффект Холла. Такой пучок можно сформировать без метаповерхности, а с помощью пространственного модулятора света.

В перечисленных работах не рассматривается распространение параксиального векторного пучка с одномерной периодической модуляцией и не рассчитывается продольная проекция СУМ для такого пучка. Кроме того, в этих работах не рассмотрен случай формирования двух вихревых гауссовых пучков с левой и правой круговыми поляризациями с помощью векторного поля с одномерной периодической модуляцией.

В данной работе мы теоретически и численно рассмотрим распространение параксиального цилиндрического векторного пучка с одномерной периодической модуляцией. Получим выражение для продольной проекции плотности спинового углового момента на любом расстоянии от перетяжки. И покажем, что у такого пучка в начальной плоскости имеется линейная неоднородная поляризация, а при распространении в пространстве формируются два пучка с левой и правой круговыми поляризациями.

1. Интенсивность и плотность спина для гауссова векторного поля с периодической одномерной модуляцией

Рассмотрим распространение параксиального гауссова векторного пучка, начальный вектор Джонса которого имеет вид:

совых пучка с левой и правой круговой поляризацией. Координаты смещения центров обоих пучков с оптической оси равны x ± = ± ( a z / к ). Интенсивность векторного поля (4) имеет вид:

x exp

[

-2

z 0 r

₄ zwq ^{( z} )|

I2

-^w- ₄ V2 q ⁽ z )|

I21     I cosh

2 a xz ₀ zq ( z ) ²

Найдем продольную проекцию спинового углового момента (СУМ) [21] поля (4). Других проекций СУМ у параксиального поля нет. Получим:

Sz = 2Im (Ex Ey ) = -

² z [ ^zq ^{( z} ) J

x

[ [ xexp -2

I ^{cos( a} x ) I

E ⁽ x , У ) = 1 ■ / x I exP ^ sin( a x ) J

x2 + y21

w ² J ,

где ( x, y ) – декартовы координаты в сечении пучка, w – радиус перетяжки гауссова пучка, α =2π / d – обратный период или пространственная частота амплитуды поля, d – период. Световое поле (1) можно назвать векторным полем с одномерной периодической модуляцией. Поле (1) можно представить как сумму двух полей с левой и правой круговой поляризацией:

cos( a x ) sin( a x )

e - ( r / w )²

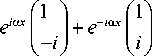
( r / w )²

- e

. (2)

В (2) r ² = x ² + y ². В начальной плоскости интенсивность поля (1) равна интенсивности гауссова пучка:

1 0 = E |² + | E y |² = exp [- 2 x^+y- I       w ²

.

Вектор Джонса для поля (1) на произвольном расстоянии z от начала будет иметь вид:

E ( x , y , z ) = - i —z ⁰— ^ 2 zq ( z )

r ² [ z 0 y I 1 exp ik 1 | -----

2 z ^ zw J q ( z )

X

x sinh

zw q ( z )

2 a xz ₀

, ^zq ^{( z} )I 2 _J

.

[ exp

1 | z 0 x q ( z ) ^ zw

² a w | V J

1 I

I + - i J

+ exp

1 I z 0 x

q ( z ) ^ zw

² a w I ~ J

i

,

где q ( z ) = 1– i × z 0 / z , z 0 = kw ²/2 – длина Рэлея, k – волновое число света. Из (4) видно, что при распространении в свободном пространстве гауссов пучок (3) будет представлять собой два смещенных по оси x гаус-

к к ² 1

[ V2 q ^{( z} )|^J

Нормированная на интенсивность плотность спи-

на будет равна:

S z

/ 1 = - tanh

2 a xz ₀

, ^zq ^{( z} )r

Получается, что в начальной плоскости у поля (1) нет спина ( S z =0), а при его распространении в свободном пространстве у поля формируется две области (4) со спином разного знака и с плотностью нормированного спина (7). Это простейший способ продемонстрировать спиновый эффект Холла и получить из линейной поляризации две круговые поляризации разных знаков.

Круговая поляризация будет в точках x , которые удовлетворяют условию S_z = ± I . А это может выполняться только при стремлении аргумента в (7) к плюс или минус бесконечности. Максимум нормированной плотности спина (7) в зависимости от расстояния z до перетяжки будет достигаться на расстоянии Рэлея z = z 0 .

Чтобы сформировать начальное световое поле (1), можно использовать метаповерхность, которая описывается матрицей преобразования поляризации, осуществляющей поворот падающего вектора линейной поляризации на угол, равный θ = αx , так как имеет место равенство:

cos( a x ) - sin( a x ) |[ 1 । [ cos( a x ) sin( a x ) cos( a x ) J ^ 0 J ^ sin( a x )

Из (8) видно, что метаповерхность поворачивает линейную поляризацию падающего пучка на угол, периодически зависящий от координаты горизонтальной оси x .

• 2.    Цилиндрический векторный пучок с несущей пространственной частотой

Световое поле (1) можно обобщить так, чтобы при распространении в свободном пространстве оно формировало не только спиновый эффект Холла, но и орбитальный. Для это рассмотрим вектор Джонса начального поля вида:

E n ( x , У )

cos( п ф + o x ) ^

I exp sin(nф + ax) J x2 + y2 w2

где φ – азимутальный угол в сечении пучка, tan(φ) = y / x , n – целое число, задающее порядок векторного поля. Поле (9) можно представить в виде двух полей с правой и левой круговой поляризациями:

co^s( n ф + а x ) I e _ ₍ r / w ) 2 sin( п ф + а x ) J

_ei ( n ф+a x )

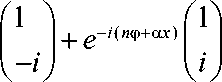
e _ ( r / w )²

Поле (1) при α =0 сводится к цилиндрическому векторному полю n -го порядка [22]. Поэтому при отличном от нуля α поле (1) можно назвать цилиндрическим векторным полем (пучком) с несущей пространственной частотой. На произвольном расстоянии z от перетяжки поле (9) примет вид:

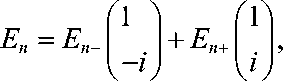
E_n ± ( x , y , z ) = -

X

C . - kr ² x exp I + in ф ± + i--

I "     2 z

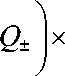
x[ I ( n _ 1)/2 ( Q ± ) _ I ( n + 1)/2 ( Q ± ) ] ,

Q. = <0* +1 ± 8 q ( z ) I

z0 y q (z) = 1 - i—, tan ф±= —---—, z           x ± az / k z 0 r | 1 ± az 0 x

2 zzw J q ( z ) 2 zq ( z )

В (11) функции Iv (x) – модифицированные функции Бесселя. Из (11) видно, что параксиальное векторное поле представляет собой два смещенных с оптической оси вихревых пучка с центрами фазовых сингулярностей (центрами вихрей) в точках x ± = ± (az / k) и с правой и левой круговыми поляризациями. При этом точки фазовой сингулярности и нули интенсивности поля (11) совпадают. Оптические вихри вблизи этих точек будут иметь топологические заряды разных знаков, n и –n. Так как вблизи нулей интенсивности амплитуда светового поля каждой проекции будет иметь вид: (x + a + iy)n и (x - a - iy)n. Заметим, что при n =0 поле (11) точно совпадает с полем (4). У поля (9) в начальной плоскости нет ни орбитального углового момента (ОУМ), ни плотности спина. А при распространении в пространстве одно поле разделяется на два, у которых есть продольный СУМ с разными знаками и есть ОУМ, тоже с разными знаками. Причем там, где спин отрицательный (левая круговая поляризация), там топологический заряд и ОУМ положительные, а где спин положительный (правая круговая поляризация), там ОУМ и топологический заряд отрицательные. Суммарный спин и ОУМ у всего поля остаются равными нулю, как и для начального поля (9).

а)

б)

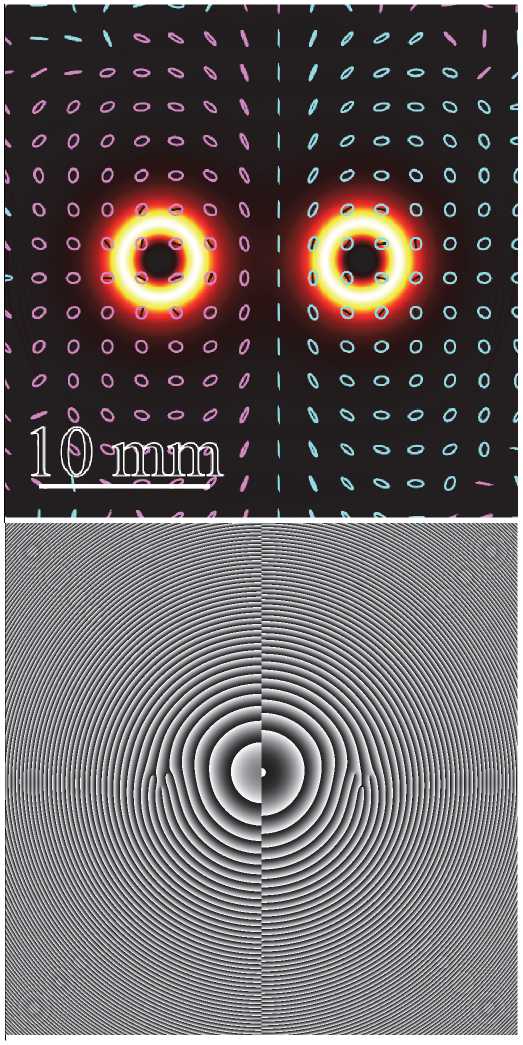
Рис. 1. Распределение интенсивности для пучка (9) при n = 3 и α = 0,001k на расстоянии z 0 от перетяжки, показанное в виде белых колец (а), и распределение поляризации по сечению пучка, показанное в виде эллипсов (левые эллипсы с правой поляризацией S z > 0 и правые эллипсы с левой поляризацией S z < 0); распределение фазы одной проекции светового поля E x (б). Размер кадров – 30×30 мм

На рис. 1 показаны рассчитанные с помощью преобразования Френеля для длины волны 532 нм распределения интенсивности (белые кольца) (а) и фазы поля Ex (б) для пучка (9) при n =3 и α = 0,001k на рас- стоянии z0 от перетяжки. Распределение поляризации на рис. 1а показано в виде левых (Sz >0) и правых (Sz <0) эллипсов. Из рис. 1а видно, что в распределении интенсивности видны два световых кольца, внутри которых поляризация почти круговая и с разными знаками (вблизи левого кольца – правая круговая поляризация, а вблизи правого кольца – левая круговая поляризация). На рис. 1б видно, что справа имеются три винтовых дислокации, подтверждающие, что топологический заряд поля Ex для правого кольца равен n =3. Слева на рис. 1б у фазы имеются три винтовых дислокации противоположенного знака, подтверждающие, что у поля Ex топологический заряд равен n =–3.

• 3.    Расчет металинзы для формирования двух пучков со спином разного знака

Как уже отмечалось (8), поле (1) можно сформировать с помощью метаповерхности. Метаповерхность должна описываться матрицей

( cos a x - sin a x

R ( x ) = 1 .

^sin ax   cos ax преобразования вектора поляризации падающего поля, где α обратно пропорционально периоду структуры вдоль оси x. При плоской падающей волне с линейной поляризацией вдоль оси x на выходе будет пучок с направлением поляризации, зависящим от координаты x (8).

На рис. 2 показана поляризация пучка (1) при α = π /2 в обратных микрон, так как x измеряется в мкм.

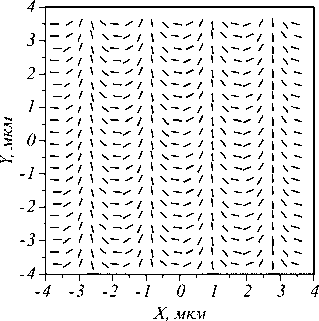
Рис. 2. Направление линейной поляризации в поле (1)

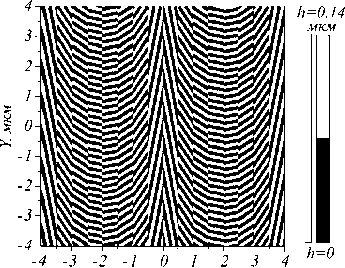
На рис. 3 показан рельеф метаповерхности, реализующей матрицу пребразования R ^ˆ( x ) (8) при α = π /2 в обратных микрон.

Период метаповерхности на рис. 3 равен 4 мкм. Размер всей метаповерхности был выбран 8×8 мкм, он рассчитан на длину волны падающего света λ =633 нм. Метаповерхность представляет собой полосы с дифракционными решётками с субволновым периодом 220 нм (110 нм канавка, 110 нм выступ), которые повернуты на угол xα /2+ π /2 по отношению к оси x. Каждый период разбит на 8 полос, в которых угол ди- фракционных решеток постоянный. Вектор поляризации поля поворачивается на двойной угол поворота линий решеток, что видно из сравнения рис. 2 и 3. Высота рельефа равна 140 нм, показатель преломления решеток n = 4,352 + 0,486i (аморфный кремний).

X, мкм

Рис. 3. Бинарный рельеф метаповерхности.

Моделирование проводилось с помощью метода FDTD и с помощью преобразования Рэлея– Зоммерфельда. Вначале с помощью FDTD рассчитывалось, как распространяется свет через метаповерхность, и на расстоянии λ от метаповерхности получалось конечное поле Ex и Ey , которое затем подставлялось на вход преобразования Рэлея–Зоммерфельда. После чего рассчитывалось результирующее поле на расстоянии 50 мкм. Моделирование только методом FDTD на таком расстоянии (порядка 50 мкм) в трехмерном случае провести невозможно из-за чрезмерной вычислительной сложности. На рис. 4 показана интенсивность поля, полученного на расстоянии λ за метаповерхностью.

Видно, что после дифракционных решеток поле имеет некоторую неравномерность, однако направление поляризации соответствует распределению, полученному по формуле (1) (рис. 2). На рис. 5 показана интенсивность пучка на расстоянии 50,633 мкм от метаповерхности, рассчитанного с помощью преобразования Рэлея–Зоммерфельда.

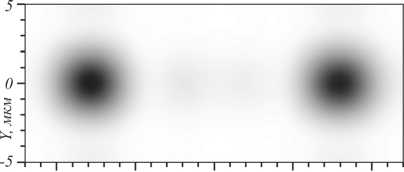
На рис. 5 видно, что на расстоянии 50,633 мкм от метаповерхности образуются два максимума интенсивности на оси x , расстояние между их центрами равно 15,86 мкм, при этом в левом максимуме интенсивности преобладает правая круговая поляризация, в правом максимуме – левая круговая поляризация. Расстояние между максимумами обусловлено периодом структуры метаповерхности (рис. 3 а ). При увеличении периода метаповерхности (рис. 3 а ) вдвое, до 8 мкм, расстояние между максимумами уменьшается примерно в два раза, до 7,64 мкм. В оба максимума интенсивности идет примерно 78,5% энергии, прошедшей через метаповерхность.

На рис. 6а показана металинза, создающая поле (9) с параметрами α = π /2 обратных микрон и n = 1. В дополнение к пространственной частоте, которая присутствует в метаповерхности на рис. 3, здесь добавлен то- пологический заряд. Поэтому вместо решетки (рис. 3) получилась решетка с «вилочкой». Хотя на рис. 6а уместилось только 2 периода такой решетки с «вилоч- кой» (с краевой дислокацией). Всего метаповерхность размером 8×8 мкм поделена на 14×14 блоков, размер каждого – 26×26 отсчетов (0,571 мкм).

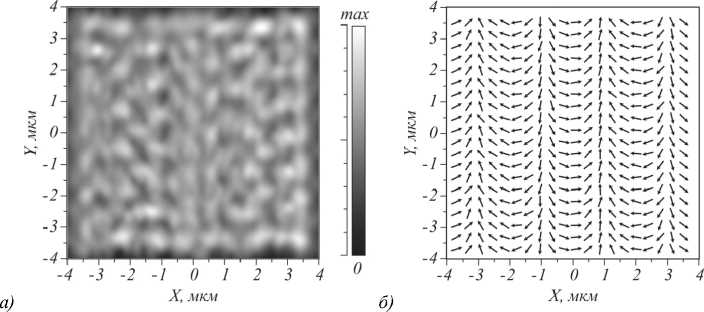
Рис. 4. Интенсивность (слева) и распределение поляризации (справа) электрического поля на расстоянии λ от метаповерхности

10        -5         0         5        10

X, мкм

X, мкм

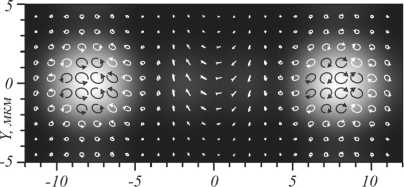
Рис. 5. Интенсивность света на расстоянии 50,633 мкм от метаповерхности (негатив) и распределение поляризации света в пучке (б). Стрелками с кружками показано направление поляризации в центре каждого кружка, причем стрелка

показывает направление вращения вектора электрического поля с течением времени

а)

X мкм

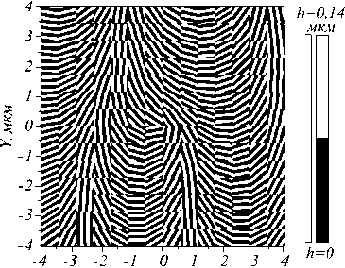
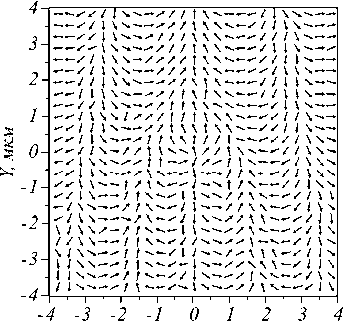
Рис. 6. Метаповерхность, формирующая цилиндрический векторный пучок (9) с пространственной несущей частотой (а), и поляризация прошедшей данную метаповерхность плоской линейно поляризованной волны на расстоянии λ от неё (б)

б)

X, мкм

На рис. 6 б показано распределение линейной поляризации на расстоянии λ от метаповерхности. Видно, что из-за краевой дислокации в центре картины на рис. 6 б возникает поляризационная сингулярность или V-точка, в которой линейная поляризация не определена.

На рис. 7 показаны результаты моделирования прохождения света через метаповерхность на рис. 6 на расстоянии 150 мкм после неё. В данном случае так же вначале рассчитывалось поле на расстоянии одной длины волны за метаповерхностью с помощью FDTD-метода, для точного учета вклада метаповерхности, а далее с помощью интеграла Рэлея– Зоммерфельда рассчитывалось поле в дальней зоне. Поскольку в данном случае формируются кольца, расстояние, на котором оба кольца сформируются и разойдутся, больше, чем для случая на рис. 5.

На рис. 7а показано распределение интенсивности на расстоянии 150 мкм после металинзы на рис. 6а. Видно, что имеются три световых пучка: централь- ный и два световых кольца слева и справа от центрального пучка. Кольцевые пучки неоднородные по интенсивности из-за того, что в метаповерхности учтены только два периода решетки. На рис. 7б показано распределение эллипсов поляризации на расстоянии 150 мкм после метаповерхности на рис. 6а. Оба кольца, сформированные в дальней зоне (рис. 7а), имеют эллиптическую и круговую поляризацию – свет с правой круговой поляризацией формирует кольцо в отрицательной зоне оси x (слева), а свет с левой круговой поляризацией формирует правое кольцо. В распределении фазы на рис. 7в видны «вилочки» на месте минимумов интенсивности двух колец, что указывает на наличие оптических вихрей (винтовых дислокаций) с топологическими зарядами –1 (слева) и 1 (справа).

а)

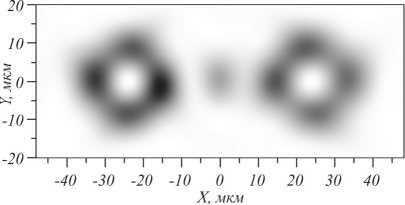
в) Рис.

б)

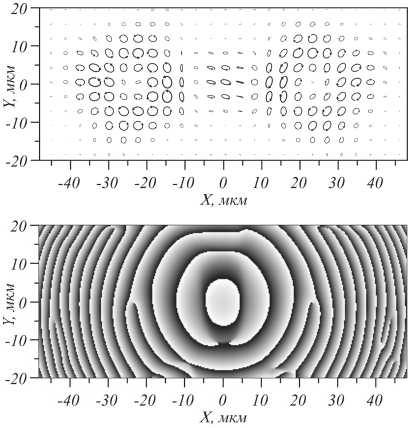
7. Интенсивность цилиндрического векторного пучка

с несущей частотой, сформированного металинзой (а) (негатив), поляризация в данном пучке, изображенная эллипсами со стрелкой (б). Каждый эллипс описывает вращение вектора электрического поля с течением времени. На рисунке (в) представлена фаза компоненты E y пучка

Заключение

В данной работе начальное векторное поле с одномерной периодической модуляцией сформировано с помощью метаповерхности в тонкой пленке аморфного кремния для длины волны 633 нм. Метаповерхность состоит из бинарных субволновых решеток с периодом 220 нм, которые периодически меняют свое направление и реализуют в совокупности одномер- ную дифракционную решетку. Падающее на такую метаповерхность световое поле с линейной поляризацией преобразуется в два расходящихся под некоторым углом световых пучка, один из которых имеет левую эллиптическую поляризацию, а второй – правую эллиптическую поляризацию. Дифракционная эффективность такой решетки – почти 80%. Также показано, что векторный цилиндрический пучок с несущей пространственной частотой можно сформировать с помощью метаповерхности с рельефом в виде решетки с «вилочкой». При освещении такой метаповерхности светом с линейной поляризацией в прошедшем поле формируются два световых кольца с левой и правой круговой поляризациями. Это простейшие метаповерхности, которые с высокой эффективностью создают спиновый эффект Холла в параксиальных лазерных пучках.

Работа выполнена при поддержке Российского научного фонда (грант № 23-12-00236) в части теории и моделирования и по государственному заданию НИЦ «Курчатовский институт» в частях «Введение» и «Заключение».