Спиновый угловой момент и спектр угловых гармоник двухпорядковых поляризационных вихрей в остром фокусе
Автор: Ковалв А.А., Котляр В.В.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 4 т.47, 2023 года.
Бесплатный доступ
Исследован спиновой угловой момент двухпорядковых цилиндрических векторных пучков в остром фокусе. Такие пучки являются обобщением стандартных цилиндрических векторных пучков, поскольку у разных поперечных компонент поля порядок поляризации тоже разный. На основе теории Ричардса-Вольфа получено выражение для распределения плотности продольной составляющей спинового углового момента. Показано, что если порядки поляризации имеют разную чётность, то в остром фокусе возникает спиновый эффект Холла, то есть формируются чередующиеся области с положительным и отрицательным спиновым угловым моментом, хотя начальное поле имело линейную поляризацию. Исследован спектр угловых гармоник всех компонентов сфокусированного светового поля, и определены преобладающие угловые гармоники. Пренебрегая несущественными гармониками, определена форма распределения продольной составляющей плотности спинового углового момента и показана возможность формирования фокального распределения, в котором области с положительным и отрицательным спиновым угловым моментом находятся на кольце в виде чередующихся пар или разделены по разным полуокружностям.
Цилиндрический векторный пучок, двухпорядковый цилиндрический векторный пучок, острый фокус, теория ричардса-вольфа, спиновый угловой момент, оптический спиновой эффект холла, спектр угловых гармоник
Короткий адрес: https://sciup.org/140301829
IDR: 140301829 | DOI: 10.18287/2412-6179-CO-1282
Текст научной статьи Спиновый угловой момент и спектр угловых гармоник двухпорядковых поляризационных вихрей в остром фокусе
В микромашинах элементы могут приводиться в движение с помощью света [1, 2]. Это требует разработки оптических пинцетов, подходящих для управляемых элементов в зависимости от их формы, материала и траектории движения. В работе [3] рассматриваются способы управления движением различных частиц при воздействии на них оптическими силами и моментами остросфокусированных лазерных пучков.
Как правило, световой пучок выходит из лазера с Гауссовой формой поперечного сечения. Затем для определённых приложений, таких как оптический захват, оптическая передача данных, лазерная сварка, пучок должен быть преобразован для достижения требуемой формы. Это привело к развитию огромного направления современной оптики – формирование лазерных пучков (beam shaping) [4].
Различные методы разрабатываются для формирования пучков как внутри резонатора, так и вне его [5], с использованием рефракционных или дифракционных оптических элементов. При этом может ставиться задача формирования пучков, которые сохра- няют свою форму на протяжении всего распространения [6] или в некоторой конкретной области, например, в фокальной плоскости [7].
При оптическом захвате частицы может возникнуть необходимость не только захватить её в опре-дёленной точке, но и чтобы она совершала какие-то движения. Например, частицу можно заставить двигаться по какой-то траектории или вращаться вокруг собственного центра. Такое вращение происходит, когда свет обладает спиновым угловым моментом (СУМ) [8], то есть если поляризация нелинейная. Таким образом, помимо задачи формирования распределения интенсивности пучков, может стоять задача формирования распределения СУМ. Помимо оптического захвата, СУМ может использоваться в качестве информации при оптической передаче данных [9].
В параксиальном приближении формирование интенсивности может быть выполнено для одной поперечной компоненты поля с однородной поляризацией. Однако для формирования СУМ нужно формировать обе поперечные составляющие поля и регулировать фазовую задержку между ними. Проблема усложняется в условиях острой фокусировки.
Недавно было замечено, что при острой фокусировке линейно поляризованного светового пучка вблизи фокуса возникают области с эллиптической поляризацией [10]. Поскольку в фокусе сформировались области с отрицательным и положительным СУМ, это является проявлением оптического спинового эффекта Холла. Позже этот же эффект был обнаружен для остро сфокусированного цилиндрического векторного пучка высокого порядка (поляризационного вихря) [11]. В [11] продольная составляющая СУМ распределена по кольцу и состоит из чередующихся областей с положительными и отрицательными значениями. Цилиндрические векторные пучки имеют вектор Джонса J = [cos m φ, sin m φ], где φ – угловая полярная координата, а m – порядок поляризации (для m = 1 – радиальная поляризация). Дальнейшим обобщением цилиндрических пучков являются пучки с двухпорядковой поляризационной сингулярностью с вектором Джонса вида J = [cos m φ, sin n φ], где m ≠ n [12, 13], то есть такое обобщённое векторное поле имеет разный порядок по разным поперечным координатам. Поскольку поперечные компоненты пучков с такой поляризационной сингулярностью зависят от полярной угловой координаты как фигуры Лиссажу, в работе [12] такие пучки названы пучками Лиссажу. Сингулярности, описываемые фигурами Лиссажу, также встречались и в полихроматических векторных полях [14]. Для монохроматических пучков в [12] обнаружено, что их СУМ может иметь поперечные составляющие (в зависимости от чётности порядков сингулярности). Недавно мы также изучали такие поля с V-точками и для ряда значений m и n аналитически установили индекс Пуанкаре–Хопфа [15].
В данной работе на основе теории Ричардса– Вольфа [16] исследуется продольная составляющая СУМ светового поля с двухпорядковой поляризационной сингулярностью в остром фокусе. Получено выражение для комплексной амплитуды вблизи фокуса и на основе этого выражения получена формула для продольной составляющей СУМ. Установлено, что она может быть отлична от нуля только для порядков m и n разной чётности. Для определения формы распределения продольной составляющей СУМ проведено разложение светового поля в фокусе в спектр угловых гармоник и оценён вклад каждой угловой гармоники. Установлено, что если фокусируемое световое поле имеет не кольцевую форму, а однородную (постоянную) или затухающую (от центра к краям) Гауссову форму, то спектр угловых гармоник состоит в основном из m -й и n -й угловых гармоник, которые на порядок превосходят остальные гармоники. Это позволило предсказать форму распределения продольной составляющей СУМ в фокусе. В качестве примера получено распределение на кольце, где области с положительным и отрицательным СУМ чередуются попарно.
1. Световое поле с двухпорядковой поляризационной сингулярностью вблизи острого фокуса
В [15] исследовано обобщение цилиндрических векторных пучков, когда порядки поляризации поперечных компонент поля E x и E y различаются. Амплитуда вектора электрической напряжённости такого поля определяется выражением
, х ( cos m q i E ( 9 , q ) = A ( 9 )1 . Vl, ^ sin n q J
где E – вектор напряженности электрического поля, φ – азимутальный угол в начальной плоскости, ( m , n ) – порядок поляризации (два целых числа), θ – полярный угол, характеризующий наклон световых лучей к оптической оси, A (θ) – амплитуда начального поля как функция угла наклона лучей к оси. Направления векторов электрической напряжённости для одинаковых и разных порядков m и n , в том числе с одинаковой и разной чётностью, показаны на рис. 1.
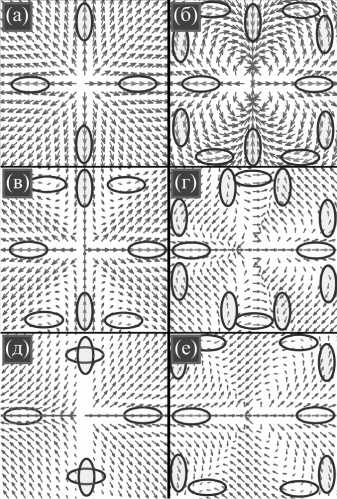
Рис. 1. Стандартная радиальная поляризация (m = n = 1) (а), радиальная поляризация третьего порядка (m = n = 3) (б), двухпорядковые поляризационные сингулярности с одинаковой чётностью: m = 1, n = 3 (в), m = 4, n = 2 (г), и двухпорядковые поляризационные сингулярности с разной чётностью: m = 1, n = 2 (д), m = 2, n = 3 (е). Для радиальной поляризации (а) вектор напряжённости горизонтален при двух значениях азимутального угла φ (0 и π) и вертикален тоже при двух углах (π/2 и 3π/2). Для радиальной поляризации третьего порядка (б) имеется шесть углов с горизонтальным направлением поляризации и шесть углов с вертикальным направлением. Для полей с двухпорядковой поляризационной сингулярностью порядка (m, n) (m ≠ n) имеется 2n углов с горизонтальным направлением поляризации и 2m углов с вертикальным направлением (в вырожденных случаях эти направления совпадают, то есть вектор напряжённости равен нулю, как на вертикальной оси на рис. д)
В нашей работе [17] получены выражения для декартовых компонент линейно поляризованного оптического вихря, сфокусированного апланатической системой. Если оптический вихрь с топологическим зарядом m линейно поляризован вдоль оси x , то во входной плоскости электрическое поле определяется выражением
E ( 9, ф ) - A ( 9 ) exp ( im ф )
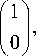
тогда как вблизи острого фокуса комплексная амплитуда равна
' Ex (p,* , z )-
- - 1 i m e m * ( 2 1 0, m + e 2* 1 2, m +2 + C * 1 2, m -2 ) ,
2 (3)
E y ( p,* , z ) - 1 i m e m * ( e - 2 i * 1 2, m -2 - e 2* 1 2, m +2 ) ,
[ Ez (p, *, z) - zme'm * (e--* 11, m-1 - e-* 11, m+1), где (ρ, ψ, z) – цилиндрические координаты с началом в фокусе.
Функции I ν,µ в (3) определяются следующим образом:
Г X 9 ^ <9 ^
I у > ц - 2 kf J sin I — I cos 3 v I — I cos 1/2 ( 9 ) x
0 v 2 ) v 2 )
xA (9) e-kz cos9 J,(kr sin 9) d 9, где k =2π /λ – волновое число монохроматического света с длиной волны λ, f – фокусное расстояние линзы, α – максимальный угол наклона лучей к оптической оси, определяющий числовую апертуру аплана-тической линзы NA= sin α, Jν() – функция Бесселя первого рода ν-го порядка.
Поле (1) можно представить в виде суперпозиции четырёх линейно поляризованных оптических вихрей. Тогда, используя (3) и аналогичное выражение для поляризации вдоль y , получим компоненты поля с поляризацией (1) вблизи острого фокуса:
E x ( p , * , z ) - - 2 i m + 1 { 2 1 0, m cos m у + 1 2, m +2 cos [ ( m + 2 ) *] + 1 2, m -2 cos [ ( m - 2 ) *] } + + 2 i n + 1 { 1 2, n +2 cos [ ( n + 2 ) *J - 1 2, n -2 cos [ ( n - 2 ) *] } ,
E y ( P , * , z ) - - 2 i n + 1 { 2 1 0, n sin n * - 1 2, n +2 sin [ ( n + 2 ) *] - 1 2, n -2 sin [ ( n - 2 ) *] } +
<
+ 2 im + 1 { 1 2, m -2 sin [ ( m - 2 ) *J - 1 2, m +2 sin [ ( m + 2 ) *] } ,
E z ( p , * , z ) - im { 1 1, m -1 cos [ ( m - 1 ) *] - 1 1, m +1 cos [ ( m + 1 ) *] } +
+ i n { 1 1, n +1 cos [ ( n + 1 ) *] + 1 1, n -1 cos [ ( n - 1 ) *] } .
Заметим, что выражение для компонент поля в остром фокусе начального поля (1) были получены в [12], но для дальнейшего анализа мы записали (5) в терминах функций (4), поскольку они, как показано ниже, позволяют определить свойства спектра угловых гармоник вблизи острого фокуса.
Продольная составляющая спинового углового момента определяется следующим образом [18]:
S z - 2Im { E X E y } . (6)
Для простоты предположим, что функции A (θ) вещественны. Тогда все интегралы I ν,µ также вещественны в фокальной плоскости ( z =0). Подставляя поперечные компоненты поля (5) в (6), получим следующее выражение для СУМ:
4 1 0, m I 0, n cos m * sin n * -
- 2 1 0, m l 2, n +2 cos m * sin [ ( n + 2 ) *] -
S z - 2lm { in - m } x <
- 2 1 0, m l 2, n -2 cos m * sin [ ( n - 2 ) *] + + 2 1 0, n I 2, m +2 sin n * cos [ ( m + 2 ) *] + + 2 1 0, n I 2, m -2 sin n * cos [ ( m - 2 ) *] +
+ ( I 2, n +2 I 2, m +2 + I 2, n -2 I 2, m -2 ) sin [ ( m - n ) *] -- ( 1 2, m +2 1 2, n -2 + 1 2, m -2 1 2, n +2 ) sin [ ( m + n ) *]
Это выражение громоздко, но из него видно, что СУМ может быть отличен от нуля, только если порядки поляризации n и m имеют разную чётность.
Когда чётность одинакова для обоих порядков, поляризация в фокусе линейна, так как, согласно (5), как E x , так и E y пропорциональны i m +1 (или i n +1)
умноженному на некоторую вещественную функцию. Вблизи центра ( r << λ), если n > m ≥ 2, поперечные составляющие E x и E y , примерно пропорциональны вектору J = [cos ( m – 2)φ, – sin ( m – 2)φ]. Если m > n ≥ 2, то они пропорциональны вектору J = [cos ( n – 2)φ, –sin ( n – 2)φ]. Таким образом, в центре генерируется поляризационная сингулярность типа седла [19].
Уравнение (7) трудно анализировать, не зная, какие слагаемые вносят наибольший вклад. Поэтому далее разложим поле вблизи фокуса на угловые гармоники и изучим спектр этих гармоник.
2. Баланс энергии светового поля вблизи острого фокуса
Сначала установим спектр угловых гармоник в остром фокусе линейно поляризованного света. Согласно (3), если входное поле поляризовано вдоль оси x , то компонента E x электрического поля вблизи фокуса состоит из трёх угловых гармоник порядков m , m – 2, m + 2. Компонента E y состоит только из двух угловых гармоник порядков m – 2 и m + 2, а компонента E z состоит из двух угловых гармоник порядков m – 1 и m + 1. Каждая гармоника пропорциональна функции I ν,µ из (4). Следовательно, такая гармоника имеет следующую энергию W ν,µ (Приложение А):
- |2
Ww = 4к f 2 J sin 2 v+ 1 l-l cos 5-2 v l-l| A ( 9 )| d 9 . (8) о V 2 J V 2 J
Согласно этому выражению, энергия угловой гармоники не зависит от расстояния z до фокальной плоскости и от топологического заряда оптического вихря, определяющего индекс µ. Таким образом, при распространении светового поля ОУМ-спектр не меняется.
Интегралы (8) могут быть вычислены аналитически только в простых случаях, но, тем не менее, можно оценить вклад каждой угловой гармоники. Например, если фокусируемое поле является однородным полем с постоянной амплитудой A (θ) ≡ 1, то
- (
W >^- 4 л / 2 J sinl ■ 0 V
a
W 1, ц = 4 л f 2 J sin 0
91 4 ,
— d 9 = -^ 2 1 - cos' . 2 J 3 4
. 6I -
* V 2
, (9)
- I з| - |
— cos 3 — d 9 -
2 J V 2 J
1 + 2 cos 2 1 -
V 2
9I - cos
2 J
-
2 /*2 ’ 4 I —
= —л f 2 sin 4 —
-
3 V 2
a
W 2,ц - 4 л f 2 J sin
— I cos[ — | d 9 = —л f 2 sin 61 — |. (11) 2 J V 2 J 3 V 2 J
Согласно (3) составляющая поля E x состоит из трёх угловых гармоник амплитуда которых пропорциональна функциям I 0 m I 2 m +2 /2 I 2 m –2 /2. Компонента E y является суперпозицией гармоник описываемых функциями I 2 m +2 /2 и I 2 m –2 /2. И наконец компонента
E z является суперпозицией гармоник описываемых функциями I 1 m +1 и I 1 m –1 . Следовательно полная энергия поля в фокусе равна
W - I W 0, m + 1 W 2, m +2 + 1 W 2, m -2 | +
V 44
+ | 1 W 2, m +2 + 1 W 2, m -2 I + ( W 1,m +1 + W 1,m -1 ) ■
I 4 . 4 . J ..
Скобки в (12) обозначают соответственно энергии угловых гармоник в компонентах поля E x , E y и E z . Поскольку I 2, m +2 = I 2, m –2 и I 1, m +1 = I 1, m –1 , получим
W - Wo,m + W2,m+2 + 2W1m+1 .(13)
Подстановка уравнений (9 – 11) в уравнение (13)
приводит к следующему выражению:
4 .
W - 3 л f 2
1 - cos 6
4 1 a I
+ — л f 2 sin 6 — +
3 V 2 J
+— л f sin4 —
1 + 2 cos 2
После упрощений получим
W - 2 л f 2 ( 1 - cos a ) .
Это выражение равно площади части сферы радиуса f , ограниченной полярным углом α. То есть если световое поле с единичной амплитудой сходится в фокус от сферической поверхности с числовой апертурой sin α, то это поле имеет энергию, определяемую уравнением (15). Таким образом, составлен баланс, когда энергия входного поля равна сумме энергий всех угловых гармоник всех трёх декартовых компонент электрического поля в фокусе.
В предельном случае, когда числовая апертура близка к единице, то есть α ≈ π/2, получаем W 0,μ = (7/6)π f 2, W 1,μ = (1/3)π f 2, W 2,μ = (1/6)π f 2. Вся энергия совпадает с площадью полусферы: W = W 0, m + W 2, m +2 + 2 W 1, m +1 = 2π f 2. Таким образом, полная энергия входного поля W распределяется в фокальном поле в пропорциях, показанных на рис. 2. На продольную составляющую E z приходится треть энергии W /3, а на поперечные составляющие – 2 W /3: E x (5 W /8) и E y ( W /24). Энергия компоненты E x распределяется на угловую гармонику m -го порядка (7 W /12) и на гармоники порядков m – 2 и m + 2, каждая из которых имеет энергию W /48. Энергия компоненты E y распределена поровну по угловым гармоникам порядков m – 2 и m + 2, каждая из которых имеет энергию W /48. Энергия компоненты E z распределена поровну по угловым гармоникам порядков m – 1 и m + 1, каждая с энергией W /6.
Очевидно, что при линейной поляризации начального поля вдоль оси y распределение энергии такое же, но основная часть (7 W /12, или 58 %) приходится на m -й порядок угловой гармоники составляющей Е у .
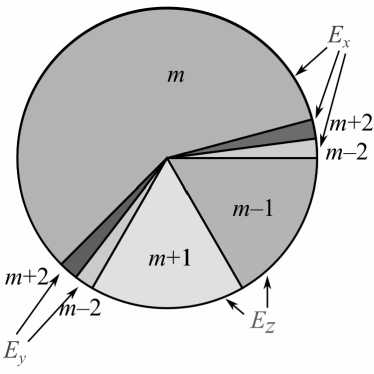
Рис. 2. Распределение энергии остросфокусированного линейно поляризованного оптического вихря по компонентам поля и по угловым гармоникам
Приведённые выше соотношения энергий могут измениться, если напряжённость начального поля не постоянна, то есть если A (θ) ≠ 1. Однако если амплитудная функция A (θ) спадает от центра к периферии, то вклад угловой гармоники m -го порядка становится ещё больше. Действительно, если апертура ограничена углом α, то энергия угловых гармоник порядков m +2 и m –2 по отношению к энергии центральной гармоники m -го порядка равна
W 2, m = sin 6 ( a/2 ) = sin 4 («/ 2 ) (16)
W o,m 1 - cos 6 ( a/2 ) 1 + cos 2 (a/ 2 ) + cos 4 ( a/2 )
Когда α уменьшается от π /2 до 0, числитель также уменьшается, а знаменатель увеличивается, то есть это соотношение энергий убывает. Например, если α = π /2, то W 2, m / W 0, m = 1/7 ≈ 0,143, но уже даже при sin α = 0,95 получается W 2, m / W 0, m ≈ 0,057, то есть почти вся энергия направляется в центральную гармонику m -го порядка.
Определим теперь спектр угловых гармоник для светового поля с двухпорядковой поляризационной сингулярностью (1). Это входное поле состоит из четырёх оптических вихрей порядков m , – m , n и – n . В остром фокусе каждый из этих вихрей расщепляется на несколько гармоник с установленными выше энергиями. Предположим для простоты, что α = π /2 и что эти гармоники не совпадают друг с другом. Тогда энергия распределяется в пропорциях, показанных на рис. 3, на котором показаны спектры угловых гармоник компонент E x , E y и E z .
Как видно из рис. 3, угловые гармоники порядков m ±2 и n ±2 имеют относительно малую энергию, которая в 28 раз меньше энергии порядков m и n , причём эта энергия становится еще меньше, когда апертурный угол начинает убывать от α = π /2.
S z - 2Im { in m } 1 0,m l 0, n cos ( m v ) sin ( n v ) . (17)
Отсюда видно, что СУМ равен нулю при следующих значениях полярной угловой координаты ψ:
V1,p = —, P = 0,-,2n -1, n (18)
л + 2 л q v2,q = —-----, q = 0,...,2m-1.
Часть углов Ψ 1, p может совпадать с частью углов Ψ 2, p . Например, если n =2 m , получим:
S z - 4Im { im } 1 0, m l 0,2 m sin ( m v ) cos 2 ( m v ) . (19)
Следовательно, формируется 4 m линий с нулевым СУМ, которые идут от начала координат под полярными углами
= ^ p , (20)
2m где p =0, 4m – 1.
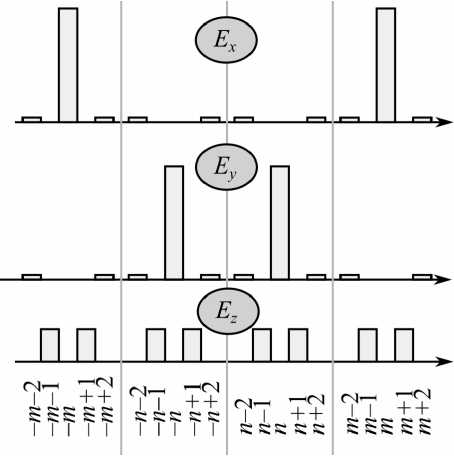
Рис. 3. Распределение энергии остросфокусированного светового поля с двухпорядковой поляризационной сингулярностью по компонентам поля и по угловым гармоникам
Однако, хотя при нечётном значении p косинус в (19) равен нулю, он возведён в квадрат. Это означает, что при этих углах СУМ не меняет знака. При чётном p СУМ меняет знак. Таким образом, распределение СУМ должно выглядеть как набор пар пятен с положительным и отрицательным СУМ.
Если m и n относительно велики и близки друг к другу, то корни синуса и косинуса не совпадают, но близки друг к другу. Поэтому СУМ меняет свой знак при каждом таком угле, но из-за пар близких нулей СУМ между ними незначителен.
4. Численное моделирование
Численное моделирование проводилось с помощью формул Ричардса–Вольфа. Рассмотрим сначала случай, когда n =2m. На рис. 4 показаны интенсивность и плотность продольной составляющей СУМ остросфокуси-рованного светового поля с двухпорядковой поляриза- ционной сингулярностью трёх различных порядков (m, n): (1, 2) (рис. 4а, б), (3, 6) (рис. 4в, г), (7, 14) (рис. 4д, е) при следующих параметрах: длина волны λ =532 нм, фокусное расстояние линзы f = 10 мкм, числовая апертура sin α = 0,95, радиальная амплитудная функция A(θ) постоянна, то есть А(θ) ≡ 1.
Как видно из рис. 4, распределение СУМ действительно состоит из чередующихся пар пятен с положительным или отрицательным СУМ. Это отличается от полученных нами ранее картин вблизи фокуса, когда пятна с положительным и отрицательным СУМ чередовались не парами [11].

Рис. 4. Распределения интенсивности |Ех|2 + |Еу|2 + |Ez|2 (а,в,д) и продольной плотности СУМ 2Im {Ex*Ey} (б,г,е) остросфокусированного светового поля с двухпорядковой поляризационной сингулярностью порядков (m, n) = (1, 2) (а,б), (m, n) = (3, 6) (в,г), (m, n) = (7, 14) (д,е) при следующих параметрах: длина волны λ = 532 нм, фокусное расстояние линзы f = 10 мкм, числовая апертура sin α = 0,95, радиальная амплитудная функция A(θ) постоянна, то есть A(θ) ≡ 1. Все рисунки имеют размер 4×4 мкм2 (масштабная метка обозначает 1 мкм). Знаки «+» и «–» (б,г,е) обозначают соответственно положительный и отрицательный СУМ
На рис. 5 показаны распределения интенсивности и продольной составляющей плотности СУМ остро-сфокусированного светового поля с двухпорядковой поляризационной сингулярностью двух различных порядков ( m , n ): (6, 7) (рис. 5 а, б ) и (16, 17) (рис. 5 в, г ) при следующих параметрах: длина волны λ =532 нм, фокусное расстояние линзы f = 10 мкм, числовая апертура sin α = 0,95, радиальная амплитудная функция A (θ) постоянна, то есть A (θ) ≡ 1.
Согласно (17), полярные углы с нулевым СУМ должны возникать парами близких углов. Из рис. 5 видно, что положительный СУМ в основном находится в верхней части, а отрицательный СУМ – в нижней. На самом деле СУМ чередуется, но между каждым пятном с положительным или отрицательным СУМ находится малая область с противоположным СУМ, которая на рис. 5 практически не видна.

Рис. 5. Распределения интенсивности |Е х |2 + |Е у |2 + |E z |2 (а,в) и плотности продольной компоненты СУМ 2Im {E x *E y } (б,г) остросфокусированного светового поля с двухпорядковой поляризационной сингулярностью порядков (m, n) = (6, 7) (а,б) и (m, n) = (16, 17) (в,г) при следующих параметрах: длина волны λ = 532 нм, фокусное расстояние линзы f = 10 мкм, числовая апертура sin α = 0,95, радиальная амплитудная функция постоянна, то есть A(θ) ≡ 1. Рисунки имеют размеры 4×4 мкм2 (а,б) и 6×6 мкм2 (в,г) (масштабная метка обозначает 1 мкм).
Знаки «+» и «–» (б,г) обозначают соответственно положительный и отрицательный СУМ
Согласно приведённой выше теории, СУМ равен нулю для порядков m и n одинаковой чётности. Расчет это подтвердил, и поляризация фокального поля оказалась линейной. На рис. 6 показаны распределения интенсивности и направления поляризации остросфокусированных световых полей с двухпорядковой поляризационной сингулярностью порядков ( m , n ) =(3, 7) (рис. 6 а ) и ( m , n ) =(5, 3) (рис. 6 б ) при тех же остальных параметрах, что и на рис. 4 и 5: длина волны λ =532 нм, фокусное расстояние линзы f = 10 мкм, числовая апертура sin α = 0,95, радиальная амплитудная функция постоянна: A (θ) ≡ 1.
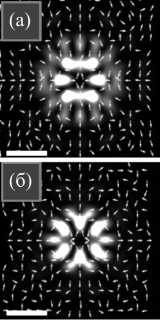
Рис. 6. Распределение интенсивности и направления поляризации остросфокусированного светового поля с двухпорядковой поляризационной сингулярностью порядков (m, n) = (3, 7) (а) и (m, n) = (5, 3) (б) при следующих параметрах: длина волны λ = 532 нм, фокусное расстояние линзы f = 10 мкм, числовая апертура sin α = 0,95, радиальная амплитудная функция постоянна: A(θ) ≡ 1.
Масштабная метка обозначает 1 мкм
На рис. 6 видно, что Ey =0 на горизонтальной оси (φ =0 и φ = π) и Ex =0 на вертикальной оси (φ =± π /2), что согласуется с уравнением (5) для комплексных амплитуд светового поля. Видно также, что в обоих случаях в центре формируется седловая поляризационная сингулярность [19].
Заключение
На основе теории Ричардса–Вольфа исследован спиновый угловой момент двухпорядковых цилиндрических векторных пучков в остром фокусе. Такие пучки являются обобщением стандартных цилиндрических векторных пучков, поскольку порядок поляризации разный для разных поперечных компонент поля. На периферии такого пучка количество областей с горизонтальной поляризацией не равно количеству областей с вертикальной поляризацией.
Установлено, что если порядки поляризации имеют разную чётность, то в остром фокусе возникает спиновый эффект Холла, то есть формируются чередующиеся области с положительным и отрицательным спиновым угловым моментом, несмотря на линейную поляризацию исходного светового поля. Если же порядки поляризации, напротив, одинаковой четности, то поляризация в остром фокусе остаётся линейной (но неоднородной).
Исследован спектр угловых гармоник линейно поляризованного поля с оптическим вихрем m -го порядка в остром фокусе. Установлено, что если исходное световое поле имеет не кольцевую форму, а однородную или Гауссову форму, затухающую от центра к периферии, то энергия угловых гармоник с порядками m ±2 в поперечных компонентах поля по крайней мере в 28 раз меньше, чем энергия угловой гармоники m -го порядка.
Получение представления о спектре угловых гармоник сфокусированного поля позволило предсказать форму распределения спинового углового момента. В качестве примера продемонстрирована возможность формирования фокального распределения, в котором области с положительным и отрицательным спиновым угловым моментом находятся на кольце и чередуются попарно либо разделены в разных полукольцах.
Работа поддержана Российским научным фондом, грант № 22-12-00137.
Список литературы Спиновый угловой момент и спектр угловых гармоник двухпорядковых поляризационных вихрей в остром фокусе
- Friese MEJ, Rubinsztein-Dunlop H, Gold J, Hagberg P, Hanstorp D. Optically driven micromachine elements. Appl Phys Lett 2001; 78: 547-549. DOI: 10.1063/1.1339995.
- Shen Y, Weitz DA, Forde NR, Shayegan M. Line optical tweezers as controllable micromachines: techniques and emerging trends. Soft Matter 2022; 18: 5359-5565. DOI: 10.1039/D2SM00259K.
- Liu J, Li Z. Controlled mechanical motions of microparti-cles in optical tweezers. Micromachines 2018; 9: 232. DOI: 10.3390/mi9050232.
- Dickey FM. Laser beam shaping: Theory and techniques. 2nd ed. Boca Raton, FL, USA: CRC Press, Taylor & Francis Group; 2014.
- Zeitner UD, Aagedal H, Wyrowski F. Comparison of resonator-originated and external beam shaping. Appl Opt 1999; 38: 980-986. DOI: 10.1364/A0.38.000980.
- Abramochkin EG, Volostnikov VG. Modern optics of Gaussian beams [In Russian]. Moscow: "Fizmatlit" Publisher; 2010. ISBN: 978-5-9221-1216-1.
- Soifer VA, ed. Methods for computer design of diffractive optical elements. New York: John Willey & Sons Inc; 2002. ISBN: 978-0-471-09533-0.
- Angelsky OV, Bekshaev AYa, Maksimyak PP, Maksimyak AP, Hanson SG, Zenkova CYu. Orbital rotation without orbital angular momentum: mechanical action of the spin part of the internal energy flow in light beams. Opt Express 2012; 20: 3563-3571. DOI: 10.1364/OE.20.003563.
- Zhang J, Yu J, Chi N. Transmission and full-band coherent detection of polarization-multiplexed all-optical Nyquist signals generated by Sinc-shaped Nyquist pulses. Sci Rep 2015; 5: 13649. DOI: 10.1038/srep13649.
- Stafeev SS, Nalimov AG, Kovalev AA, Zaitsev VD, Ko-tlyar VV. Circular polarization near the tight focus of linearly polarized light. Photonics 2022; 9(3): 196. DOI: 10.3390/photonics9030196.
- Kotlyar VV, Stafeev SS, Kovalev AA, Zaitsev VD. Spin Hall effect before and after the focus of a high-order cylindrical vector beam. Appl Sci 2022; 12(23): 12218. DOI: 10.3390/app122312218.
- Khonina SN, Ustinov AV, Porfirev AP. Vector Lissajous laser beams. Opt Lett 2020; 45(15): 4112-4115. DOI: 10.1364/OL.398209.
- Freund I. Polarization singularity indices in Gaussian laser beams. Opt Commun 2002; 201: 251-270. DOI: 10.1016/S0030-4018(01)01725-4.
- Kessler DA, Freund I. Lissajous singularities. Opt Lett 2003; 28: 111-113. DOI: 10.1364/OL.28.000111.
- Kotlyar VV, Kovalev AA, Stafeev SS, Nalimov AG, Ra-souli S. Tightly focusing vector beams containing V-point polarization singularities. Opt Laser Technol 2022; 145: 107479. DOI: 10.1016/j.optlastec.2021.107479.
- Richards B, Wolf E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc R Soc Lond A 1959; 253: 358-379. DOI: 10.1098/rspa.1959.0200.
- Kotlyar VV, Kovalev AA, Nalimov AG. Energy density and energy flux in the focus of an optical vortex: reverse flux of light energy. Opt Lett 2018; 43(12): 2921-2924. DOI: 10.1364/OL.43.002921.
- Barnett SM, Allen L. Orbital angular momentum and non-paraxial light beams. Opt Commun 1994; 110: 670-678. DOI: 10.1016/0030-4018(94)90269-0.
- Dennis MR. Topological singularities in wave fields. PhD thesis. Bristol: University of Bristol; 2001.
- Ponce de Leon J. Revisiting the orthogonality of Bessel functions of the first kind on an infinite interval. Eur J Phys 2015; 36: 015016. DOI: 10.1088/0143-0807/36/1/015016.


