Спиральная фазовая пластинка со множеством центров сингулярности

Вихревые лазерные пучки [1] продолжают напряженно исследоваться из-за их уникальных топологических свойств [2, 3] и широкого применения в квантовой информатике [4], системах беспроводной связи [5], манипулировании микрочастицами [6], зондировании атмосферы в присутствии турбулентности [7]. Впервые вихревые лазерные пучки с фазовой сингулярностью были сформированы с помощью амплитудной голограммы с «вилочкой» [8] и спиральной фазовой пластинки (СФП) [9]. Сегодня такие пучки удобно формировать с помощью пространственного модулятора света (ПМС) [10]. Лазерные пучки с фазовой сингулярностью характеризуются определенным топологическим зарядом (ТЗ) [2] и несут орбитальный угловой момент (ОУМ) [3]. Эти характеристики отражают разные стороны вихревого пучка. Если ОУМ сохраняется при распространении пучка, то ТЗ может сохраняться, а может не сохраняться при распространении [11]. Топологический заряд пучка, состоящего из линейной комбинации ОУМ-гармоник [12], определяется «топологической конкуренцией» между ними [13]. При распространении лазерного пучка с начальным дробным ТЗ могут рождаться новые оптические вихри (центры сингулярности) [14, 15]. В [16, 17] было показано, что Гауссов пучок с

внедренным в его перетяжку множеством оптических вихрей с топологическими зарядами одного знака является структурно-стабильным и при распространении изменяет только масштаб и может вращаться. В [18] рассмотрен частный случай, когда центры сингулярности (нули интенсивности) лежат равномерно на окружности (центр окружности лежит на оптической оси) в поперечном сечении Гауссова пучка. В [18] удалось получить точные выражения для ТЗ и ОУМ такого мультивихря. Измерять ТЗ можно с помощью цилиндрической линзы [19] или треугольной диафрагмы [20], а измерять ОУМ можно с помощью двух цилиндрических линз [21].

В данной работе мы рассматриваем новый оптический элемент – мультиспиральную фазовую пластинку (МСФП), которая имеет множество центров сингулярности фазы, произвольно расположенных по плоскости пластинки. В практическом плане формировать вихревой лазерной пучок с помощью МСФП можно как обычно, с помощью ПМС. Приводятся замкнутые выражения для ТЗ и ОУМ оптических вихрей, сформированных МСФП. Особенностью такой спиральной фазовой пластинки является то, что при попадании центра сингулярности на край ограничивающей диафрагмы ТЗ пучка в начальной плоскости становится полуцелым. Если все центры сингулярности попали на край диафрагмы, то ОУМ пучка будет равен нулю.

Если все центры сингулярности собраны в центре пластинки, то МСФП становится обычной СФП.

Заметим, что ранее авторы уже рассматривали пучки с несколькими сингулярностями [22]. Но в [22] были рассмотрены поляризационные сингулярности, внедренные в Гауссов пучок. В каждой точке у такого пучка поляризация линейная, но вектор поляризации изменяется по полю, аналогично как у радиальной или азимутальной поляризации. В данной работе мы рассматриваем другую ситуацию, когда Гауссов пучок с линейной поляризацией падает на фазовую пластинку с несколькими синулярностями, центры которых произвольно расположены по полю. Сходство этих работ в том, что в обеих работах в начальном поле несколько произвольно расположенных по сечению пучка сингулярностей (неопределенностей) фазы или поляризации. Оба типа таких неопределенностей приводят к изолированным нулям интенсивности в поле. А различия в том, что для случая поляризационных сингулярностей удалось только найти координаты нулей интенсивности, а для пучка с фазовыми сингулярностями удалось рассчитать ОУМ и ТЗ.

Топологический заряд поля от МСФП

Рассмотрим комплексную функцию пропускания мультиспиральной фазовой пластинки, у которой име- ются M центров фазовой сингулярности, находящихся в точках с полярными координатами (rp, фp):

E ( r , ф ) = circl | - | exp ( i V ( r , ф ) ) , v R )

M

^( r, ф) = Z Пр arctg p=1

r sin ф- r p sin ф p r cos ф- r p cos ф p

где ( r , ф , z ) - цилиндрические координаты, n_p - топологический заряд каждой отдельной сингулярности, circl( r / R )={1, r < R ;0, r > R } - функция круглой диафрагмы с радиусом R , которая ограничивает МСФП. Рассчитаем полный ТЗ светового поля в начальной плоскости, которое появляется сразу за МСФП (1), если осветить ее нормально световым пучком с радиально-симметричной амплитудой A ( r ). Для расчета ТЗ воспользуемся формулой Берри [2]:

1 ² П      д

TC = lim— f d ф— arg E ( r , ф ) = ^{r -}” 2n '     дф

1 Г Т 2t л дE (r, ф) / дф = —limIm d ф ———.

2n r —   J      E (r, ф)

Подставим в первый из интегралов выражения (3) аргумент функции (1), получим:

r ² - rr p cos ( ф-ф p ) r ² + r p - 2 rr p cos ( ф-ф p )

1 ^{2 п}       д 1 M     ^{2 n}

TC = lim— f d ф—V ( r , ф ) = —lim Z n_p f d ф ^{r -}” 2 n •     дф            2 n ^{r -}” p =1 ^J

R M 2П        R - - p cos ( ф-ф p )

= Z n_p d ф— = ^ 2 n p=1 0     R ² + r p - 2 R- p cos ( ф-ф p )

M

Znp , -p < R, p = 1,2,...M, p=1

1 ^M

-Z n p , - p = R , p = 1,2,... M ,

² p =1

N

Z np +

1 ^M

- Z n p , - p <  R , p = 1,2,... N ,

² p = N +1

r_p = R , p = N + 1, N + 2,... M .

При получении (4) воспользовались справочным интегралом [23]

n d ф

0 a + b cos ф

n

V a ² - b²

, |a| > |b|.

Из (4) следует, что если точка сингулярности фазы МСФП находится на краю диафрагмы, то ТЗ светового поля в начальной плоскости будет дробным (целым или полуцелым). Ранее авторами было показано [13], что при распространении оптического вихря с начальным дробным ТЗ могут возникать несколько сценариев эволюции такого вихря, в зависимости от близости начального ТЗ к четному или нечетному целому числу. В нашем случае механизм возникновения дробного ТЗ другой, и в данном случае начальный ТЗ может быть только целым или полуцелым. Заметим, что если в (1) вместо освещающей плоской волны,

ограниченной круглой диафрагмой, осветить СФП Гауссовым пучком, то ТЗ оптического вихря, сформировавшегося за СФП, будет равен сумме топологических зарядов всех сингулярностей:

M

TC = Z n p .

p =1

Орбитальный угловой момент пучка после МСФП

Найдем далее ОУМ светового поля (1) в начальной плоскости. Для этого воспользуемся известным выражением для расчета ОУМ и мощности пучка [21]:

го 2л     Д ту

J_z = - i f f E * —rdrd ф , ^z

0 0 ^ф

W = J JI E\ ² rdrd ф .

Для взятия производной под интегралом в (6) от поля (1) удобно переписать амплитуду поля (1) в виде:

I Г

E ( r , ф ) = circl I — I A ( r ) x

M х П p =1

I reiф - rpeiфp v ^r2 + rp2 - 2rrp cos (ф - фp)

Подставим (8) в (6), получим:

MR ₂

Jz = Z Пр Jl A(r)| rdr x p=1    0

x

2n

J d ф

r ² - rr p cos ( ф-ф _p ) r ² + r p - 2 rr p cos ( ф - ф _p )

MR

2      2n , r p < r npj A( r) rdr L   .

p =1 0               I ^0, r p ^ ^r

MR ₂

= Z n p J A ^{( r} )l ^rdr .

^p =1     r p

При получении (9) воспользовались справочными интегралами [23]:

2n

J

dx

2 n

■² - 2 a cos x |1 - a ²| ’ 2 n a

Если радиус окружности, на которой лежат центры сингулярностей, совпадает c радиусом диафрагмы ( r 0 = R ), то из (12) следует, что ОУМ пучка после СФП будет равен нулю. Однако ТЗ такого пучка будет отличен от нуля и равен 0,5 Z n_p . Простой пример оптического вихря, у которого ОУМ равен нулю, а ТЗ отличен от нуля, приведен в Приложении. Из (12) видно, что если все центры сингулярности свести в центр диафрагмы ( r p =0), то ОУМ пучка (12) будет равен ТЗ (4): J_z / W = Z n p .

Амплитуда светового поля, прошедшего МСФП

Найти амплитуду светового поля в зоне Френеля или в дальней зоне для светового поля (1) в замкнутом виде (без использования рядов) не удается. Поэтому упростим задачу и рассмотрим, к чему приводит смещение с оптической оси одного центра сингулярности оптического вихря, внедренного в перетяжку Гауссова пучка, в Фурье-плоскости сферической линзы. То есть вместо (1) рассмотрим в начальной плоскости световое поле с амплитудой вида:

I r2Y Xn

E ( r , ф ) = exp-- ( re i ^ф - r ₀ e i ^ф0 ) .                (13)

I w2 Jv

²r    cos xdx =

0 1 + a ² - 2 a cos x

1 - a~ 2n

В Фурье-плоскости сферической линзы с фокусным расстоянием f комплексная амплитуда поля (13) выражается через преобразование Фурье

a (a2 -1)

Нормированный ОУМ светового пучка с амплитудой A ( r ), прошедшего МСФП (1), будет равен выражению:

E ( P , 6 )

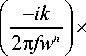
J z W

MR ₂

Z np J A(r)l rdr p=1     rp__________________

R

J| A ( r )|² rdr

да 2n r 2

x J J e w ² ( re i ^ф

) n

x

Выражение (11) для ОУМ обобщает ранее полученное авторами выражение для СФП с одним смещенным центром сингулярности [24]. Из сравнения (4) и (11) видно, что ОУМ зависит от степени близости центров сингулярности фазы МСФП к краю круглой диафрагмы радиуса R . Если центр сингулярности фазы попадает на край диафрагмы, то он «пропадает» из суммы в (11) и не дает вклад в ОУМ. Такой «крайний» центр сингулярности ( r p = R ) дает «половинный» ( n p /2) вклад в общий ТЗ пучка. В случае, если все центры сингулярности лежат на окружности радиуса r 0 , выражение (11) упрощается:

J z W

R

A(r) 2 rdr M r0

R          Z n p .

J| A ( r )|² rdr ^p =1

x exp

- ikrp f

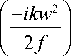
exp

cos (ф-6) Irdrdф =

kw p ) ² )f ^{- ikw} P e₆ - rL e i»» | n 2 f J Jl 2 f     w J

где k – волновое число света. Из сравнения (13) и (14) видно, что ноль интенсивности (центр сингулярности) n -го порядка в начальной плоскости, находящийся в точке с координатами ( r ₀, ф ₀, z = 0) в Фурье-плоскости, останется по-прежнему нулем интенсивности n -го порядка, но будет находиться в точке с координатами (2 / r ₀/ kw ², ф 0+ п/ 2, z = / ). То есть повернется на 90 градусов по отношению к начальному положению. ОУМ такого пучка, в котором оптический вихрь смещен с оси, уменьшается с ростом величины смещения r 0 [24]. Можно показать, что аналогичным образом будут распространяться и несколько нулей интенсивности (оптические вихри), внедренных в разные точки перетяжки Гауссова пучка. Комплексная амплитуда такого пучка на любом расстоянии от перетяжки будет иметь вид [16,17]:

M

. 1 I V2 I I -r2 1

E(r,ф) =              exPl 2 , Jx q (z) I w J      ( w2 q (z)J

r 'sin ф ' = r sin ф- r ₀ sin ф _о , r 'cos ф ' = r cos ф- r ₀ cos ф _о .

M      i ф

хП| — Pp=i I q(z)

-

. 1 np                     z rpe‘фp I , q(z) = 1 + i —, J                 z 0

Тогда в новых переменных получим вместо (17):

где z 0 = kw ² /2 – длина Рэлея.

Найдем также комплексную амплитуду поля в Фурье-плоскости для поля c комплексной амплитудой в начальной плоскости:

E ( P , 0 ) = | J^k | exp | - ' k? r o p cos( 0 - ф о ) I e ^{r ) /} w ²

12nf J   I f J

I k

x x n l - i pe0

^^^^^^

Z r L_e.o w 2 e

ⁿ да r '²

J e w ² J_n ( r ' x ) r ' dr ',

x

I r2 1 n

E ( r , ф ) = exp -      ( re ' ^ф - r ₀ e ' ^фо ) x

I w ² J                             (16)

где

1/2

x ( r ² + r ² - 2 rr cos( ф- ф о ) ) n /2

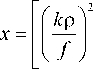
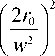
_n. kr o ^p

- 2 1     cos ( 0-ф о )

fw ²

Фурье-преобразование для поля (16) будет иметь вид:

Интеграл по r’ в (19) можно вычислить с помо-

E ( P , 0 )

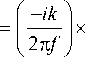
щью справочного интеграла [23]:

да 2 л      r ²

xj J e w ² exp in arctg

L

r sin ф - Г о sin ф о

x

r cos ф- r ₀ cos ф _о

J xe - px ² J _v ( cx ) dx =

x exp

- ikrp f

cos ( ф-0 ) I rdrd ф .

c ²

£^_ _e-8-p 8 p 3/2

I ( v -1)/2

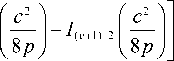
Введем новые переменные:

E ( P , 0 ) =

- ikw²

_v 16 vn f

exp l - i— r _o p cos( 0-ф _o) I e ^{r 0 /} w x ⁿ

( xw )

где I v ( x ) – модифицированные функции Бесселя. Окончательно вместо (19) получим:

k

- if p e ' ⁰

-

r

—e' ^{ф 0}

n

I ; n - 1)/2

I x ² w 2 1

I 8 J

I ( n + 1)/2

( x ² w ² 1

I ^^^^^^* ^^^^^^^^^^^^^^^^^^^^^^^^^^* I

I 8 ^J_

Из (21) следует, что как и у поля (14), так и поля (16) ноль интенсивности порядка n будет в Фурье-плоскости находиться в точке с координатами

⁽ p , ⁰ , z ) = ⁽ I fr ⁰-, ф о +^П , z = ^{f 1} .

V kw ²       2 J

То есть оба поля (4) и (16) топологически одинаковы.

Эксперимент и моделирование

На рис. 1 показана использованная экспериментальная установка. Линейно-поляризованный лазерный луч Гаусса (λ =532 нм, w 0 составляет около 5 мм) был расширен и коллимирован с помощью комбинации точечного отверстия PH (с апертурой 40 мкм) и линзы L 1 с фокусным расстоянием 350 мм. Зеркала M 1 и M 2 , а также два светоделителя B 1 и B 2 были использованы для реализации интерферометрической установки Маха – Цендера. Коллимированный лазерный пучок далее падал на дисплей пространственного модулятора света SLM (HOLOEYE LC-2012, 1024×768 пикселей), который использовался для реализации функции мультиспиральной фазовой пластинки. Оптическая система 4- f состояла из линз L 2 (фокусное расстояние f 2 = 150 мм) и L 3 (фокусное расстояние f 3 = 150 мм), а диафрагма D пространственно фильтровала лазерный пучок, генерируемый SLM.

Распределение интенсивности, сформированное в зоне Френеля на расстоянии 50 мм от фокальной плоскости объектива L 4 (фокусное расстояние f 4 =350 мм), было записано с помощью видеокамеры (3264×2448 пикселей, размер пикселя 1,67 мкм). Фильтр нейтральной плотности F использовался для выравнивания интенсивностей объектного и опорного пучков.

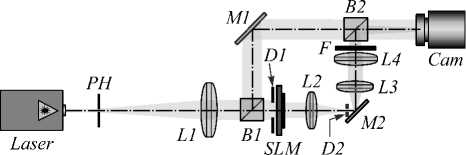
Рис. 1. Схема экспериментальной установки в виде интерферометра Маха – Цендера

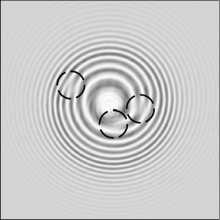
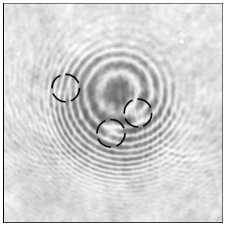
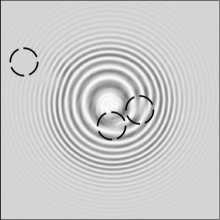
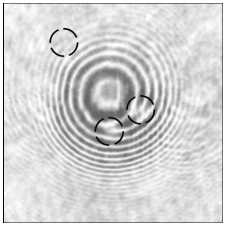
На рис. 2 показаны экспериментальные (в ,г, ж, з, л, м) и для сравнения модельные (а, б, д, е, и, к) картины сечения интенсивности пучка (а, в, д, ж, и, л) и его интерферограммы (б, г, е, з, к, м) в зоне Френеля (на 50 мм от фокуса линзы L4). Пучок был сформирован мультиспиральной фазовой пластинкой с тремя центрами сингулярности, лежащими внутри круга с радиусом 4 мм (а, б, в, г). По сбоям полос на интерферограммах (б, г) можно видеть, что в пучке присут- ствуют 3 оптических вихря с ТЗ +1 (выделены черными кружками). Таким образом, ТЗ всего пучка будет равен 3. Интересно, что если центр одного из вихрей на рис. 2 будет находиться на краю диафрагмы (д, е, ж, з), то в распределении интенсивности этот «обрезанный» вихрь не проявляется (д, ж). А на интерферограммах (е, з) он проявляется в виде сближения интерференционных полос (отмечено кружком на рис. 2e, з). Поэтому в данном случае ТЗ всего пучка дробный 2,5. Если же центр третьего вихря находится за пределами диафрагмы, то он не проявляется ни в интенсивности пучка (и,л), ни на интерферограмме (к,м). Заметим, что световые «ободки» вокруг нулей интенсивности на рис. 2а,в,д,ж,и,л были описаны в [25] и появляются из-за того, что оптический

вихрь, как воронка, «выбрасывает» интенсивность из своего центра на периферию.

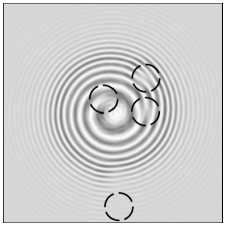
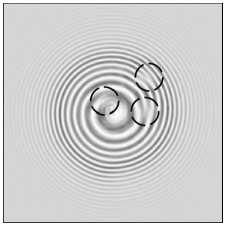
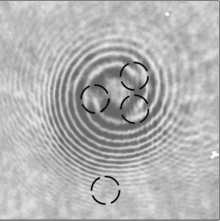
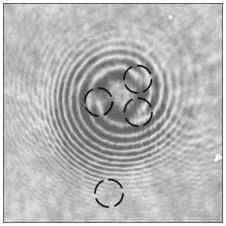
На рис. 3 показаны распределения интенсивности и их интерферограммы для пучка с 4 оптическими вихрями в зоне Френеля, сформированного мульти-спиральной фазовой пластинкой. И так же, как на рис. 2 е, з , на рис. 3 е, з видно из интерферограммы, что когда центр одного из вихрей попадает на край диафрагмы, то вместо сбоя полос на половину полосы происходит сбой меньше, чем на половину полосы (выделено кружком на рис. 3 е, з ). То есть ТЗ пучка на рис. 3 д, ж равен 3,5.

В заключение этого параграфа заметим, что эксперимент (рис. 2, 3) согласуется с теорией (4).

в)

г)

ж)

з)

л)

м)

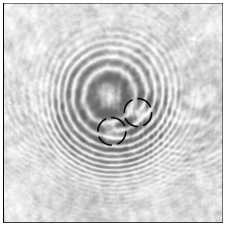
Рис. 2. Модельные (а, б, д, е, и, к) и экспериментальные (в, г, ж, з, л, м) распределения интенсивности без опорного пучка (а, в, д, ж, и, л) и с опорным пучком (б, г, е, з, к, м) на расстоянии 50 мм от фокуса линзы L4, сформированные мультиспиральной фазовой пластинкой (SLM), с тремя центрами сингулярности, находящимися внутри круглой диафрагмы радиусом 4 мм (а, б, в, г), с тремя центрами сингулярности, но один из которых находился на краю диафрагмы радиусом 4 мм (д, е, ж, з), и с тремя центрами сингулярности, но один из которых находился за пределами диафрагмы радиусом 4 мм (и, к, л, м). Размеры кадров – 10×10 мм

Заключение

Рассмотрена мультиспиральная фазовая пластинка, у которой вместо одного центра сингулярности фазы рассматриваются множество центров сингулярности одного знака, но разного порядка, расположенных в произвольных точках в плоскости спиральной пластинки. Топологический заряд такой МСФП равен сумме всех порядков каждой сингулярности, если все они лежат внут-

ри границы круглой диафрагмы. Если некоторые центры сингулярности лежат на границе диафрагмы, то их топологический заряд учитывается со множителем 1/2. Орбитальный угловой момент мульти-СФП (вернее поля, которое она формирует) зависит от расстояния каждого центра сингулярности от оптической оси (от центра пластинки или от центра круглой диафрагмы). Чем дальше от центра расположен центр сингулярности, тем меньше его вклад в общий ОУМ пучка. Если все центры

сингулярности СФП расположены на краю диафрагмы (или вне диафрагмы), то ОУМ пучка равен нулю. Если все центры сингулярности собраны в центре СФП, то ее ОУМ максимален и совпадает с ее ТЗ. Эксперимент по

формированию лазерного пучка с помощью мультиспи-ральной фазовой пластинки согласуется с предсказаниями теории и с моделированием в том, что ТЗ пучка, у которого центр лежит на краю диафрагмы, дробный.

а)

б)

ж)

в)

л)

г)

з)

м)

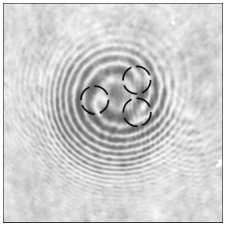
Рис. 3. Модельные (а, б, д, е, и, к) и экспериментальные (в, г, ж, з, л, м) распределения интенсивности без опорного пучка (а, в, д, ж, и, л) и с опорным пучком (б, г, е, з, к, м) на расстоянии 50 мм от фокус линзы L4, сформированные мультиспиральной фазовой пластинкой (SLM) с четырьмя центрами сингулярности, находящимися внутри круглой диафрагмы радиусом 4 мм (а, б, в, г), с четырьмя центрами сингулярности, но один из которых находился на краю диафрагмы радиусом 4 мм (д, е, ж, з), и с четырьмя центрами сингулярности, но один из которых находился за пределами диафрагмы радиусом 4 мм (и, к, л, м). Размер кадров – 10×10 мм

Заметим, что рассмотренная в этой работе ситуация, когда фазы оптических вихрей ограничены круглой диафрагмой, существенно отличается от ситуации, рассмотренной в [26], когда уже сформированный оптический вихрь (пучок Лагерра–Гаусса) проходит через круглое отверстие в непрозрачном экране. В [26] показано, что после диафрагмы в пучке формируются другие моды Лагерра–Гаусса с радиальными индексами как больше, так и меньше, чем у исходного пучка. В нашем случае тоже возникают дополнительные оптические вихри, но только если хотя бы один центр сингулярности лежит на краю диафрагмы. Если же центры всех сингулярностей (вихрей) лежат внутри диафрагмы, то ТЗ пучка не зависит от радиуса диафрагмы и равен числу вихрей с учетом их кратности.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-29-

20003, расчет топологического заряда), Российского научного фонда (грант 18-19-00595, расчет орбитального углового момента), а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (результаты моделирования).