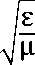Спиральная структура электромагнитных волн и стационарных электромагнитных полей

Рассматривается новое решение уравнений Максвелла, из которого следует, что электромагнитные волны и стационарные электромагнитные поля имеют спиральную структуру

Содержание

• 1.    Вступление

• 2.    Характеристика нового решения уравнений Максвелла

• 3.    Пример: цилиндрическая волна в вакууме Литература

• 1.    Вступление

• 2.    Характеристика нового решения уравнений Максвелла

Система уравнений Максвелла является одним из величайших открытий человеческого разума. В то же время известные решения этой системы уравнений обладают рядом недостатков. Достаточно сказать, что эти решения не удовлетворяют закону сохранения энергии. Такие решения позволяют некоторым авторам усомниться в достоверности самих уравнений Максвелла. Подчеркнем, однако, что эти сомнительные результаты следуют только из известного решения . Но решение уравнений Максвелла может быть иным (уравнения в частных производных имеют, как правило, несколько решений). И необходимо найти такое решение, которое не противоречит физическим законам и эмпирически установленным фактам.

Автор нашел новое решение системы уравнений Максвелла, свободное от указанных недостатков [1-4]. Это решение найдено для уравнений Максвелла, записанных в покоординатной форме, и не может быть получено в векторном виде из уравнений Максвелла, записанных в векторной форме. Это, видимо, и послужило причиной того, что предлагаемое решение до сих пор не было получено.

На основе нового решения уравнений Максвелла теоретически предсказана и экспериментально подтверждена спиральная структура электромагнитных волн и стационарных электромагнитных полей, а также показано, что спиральные структуры существуют во всех без исключения волнах и технических устройствах. Спиральность структур выражается в том, что покоординатные напряженности электрических и магнитных волн и полей изменяются в зависимости от координат и времени (для волн) по синусоидальным функциям.

Для иллюстрации на рис. 1 показана винтовая линия данного радиуса, на которой напряженность сохраняет постоянное значение. На рис. 2 показаны винтовые линии для различных значений радиуса. Прямыми линиями показаны геометрические места точек с равной фазой.

Рис. 1.

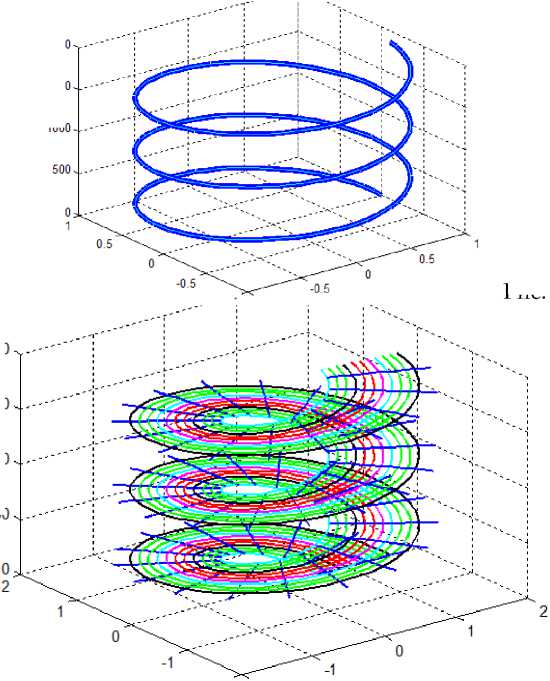
Рис. 2.

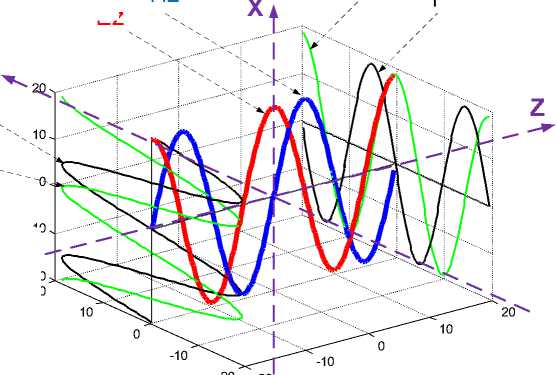
На рис. 3 показаны в декартовых координатах электрические Е и магнитные напряженности Н волны.

Ey

Y

Hx

Ex

Hz

Hy

Ez

-10

-20

Рис. 3.

Теоретические предсказания обосновываются тем, что эти функции таковы, что

• •    не противоречат закону сохранения энергии в каждый момент времени (а не в среднем), т.е. устанавливают постоянство плотности потока электромагнитной энергии во времени,

• •    выявляют сдвиг фаз между электрическими и магнитными напряженностями не только в технических устройствах, но и в волнах,

• •    объясняют существование потока энергии вдоль и внутри (а не снаружи) провода, равного потребляемой мощности,

• •    объясняют закрученность света, т.е. появление орбитального углового момента, при котором поток энергии не просто летит вперед, а крутится вокруг оси движения - см. рис. 4, где на среднем фрагменте показан незакрученный свет, а на верхнем и нижнем фрагментах – свет, закрученный в ту или иную сторону. Можно сравнить этот рис. 4 с рис. 2, построенном на основе найденного решения.

  

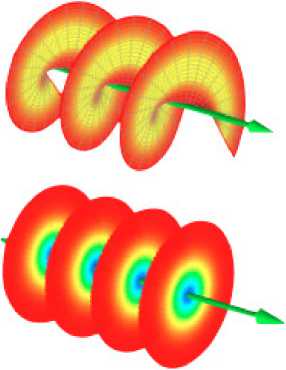
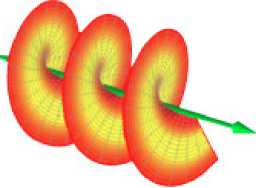
Рис. 4.

Теоретические предсказания, как следствие решения уравнений Максвелла, подтверждаются экспериментальными наблюдениями и объяснениями экспериментов, которые до сих пор не были обоснованы, в т.ч.

• •    сохранение величины мгновенной (а не в среднем) электромагнитной энергии в волне,

• •    сдвиг фаз между электрическими и магнитными напряженностями не только в технических устройствах, но и в волнах,

• •    закрученность света, т.е. появление орбитального углового момента, при котором поток энергии не просто летит вперед, а крутится вокруг оси движения,

• •    существование потока энергии вдоль и внутри (а не снаружи) провода, равного потребляемой мощности,

• •    существование э.д.с., необъяснимых электромагнитной индукцией,

• •    сохранение энергии в диэлектрике конденсатора, освобожденного от обкладок,

• •    вращающий момент в проводе и двигатель Мильроя,

• •    однопроводная передача энергии,

• •    постоянное восстановление энергии магнита,

• •    плазменный кристалл,

• •    поток электромагнитной энергии внутри провода,

• •    момент импульса в магните,

• •    заряд конденсатора продольным магнитным полем,

• •    заряд конденсатора круговым магнитным полем,

• •    э.д.с. в проводе, находящемся в неоднородном продольном магнитном поле,

• •    э.д.с. в проводе, находящемся в круговом магнитном поле,

• •    э.д.с. в проводе, находящемся в в поперечном магнитном поле,

• •    магнитное поле в заряженном конденсаторе,

• •    неэлектромагнитная индукция (как следствие магнитодвижущей силы),

• •    продольная магнитная напряженность в полости трубчатого проводника,

• •    поток энергии, как электродвижущая сила,

• •    природа потенциальной энергии конденсатора,

• •    сохранение энергии в замкнутом магнитопроводе.

• 3. Пример: цилиндрическая волна в вакууме

Рассмотрим в качестве примера решение системы уравнений Максвелла для цилиндрической волны в вакууме. Здесь рассматриваются уравнения Максвелла в системе СГС следующего вида:

rot(E)+ ^ — = 0, (1) c 5t rot(H) -^ = 0 (2) div(E )= 0, (3) div(H )= 0, (4) где   H , E - магнитная и электрическая напряженности соответственно, У - токи смещения.

В системе цилиндрических координат r, ф, z эти уравнения имеют вид:

• E, д е   1 г ^Е    а е

111— 0 , г    Э r   r д ф    д z

• 1    дEz дЕф _ dH -----— v-----, r дф   дzdt

де  дЕdH

----r_--z_ — v----, дz    д r dt еф дE 1 aEdH

1— v, r    д r   r дф

H r- ₊д Н т + 1 .!^+ ^{д H}z — 0 r д r r д ф

• 1    д H z д Н ф

  -----— q----j r дф    дzdt

^a-^ = '

• ^H , ^{д H} ф 1 д HdE

• 1—    q-----, r д r   r дф

  
  

где

E_r, Е _ф , E z - электрические напряженности,

Hr, Hф, Hz - магнитные напряженности, v — - ^ c j(9)

q — E c,(10)

Для сокращения записи в дальнейшем будем применять следующие обозначения:

co — со^аф + xz + rot),(11)

si — 8т(аф + xz + rot),(12)

где а, x, to — некоторые константы. Представим неизвестные функции в следующем виде:

H r . — h r ( r )t o ,                                             (13) H Ф • — А ф ( r ) si ,                                                (14) H z . — h z ( r ) si ,                                                (15) E r • — e r ( r V ,                                               (16)

^Е Ф^- = %⁽ r ) ^co ,                                              (17)

E z - = e z ( r ) co ,                                                    (18)

где h ( r ), e ( r ) - некоторые функции координаты г .

Непосредственной подстановкой можно убедиться, что функции (13- 18 ) преобразуют систему уравнений (1-8) с четырьмя аргументами г , ф, z , t в систему уравнений с одним аргументом r и неизвестными функциями h ( r ), e ( r ) . Эта система уравнений имеет следующий вид:

r () + e r ( r )     ф а X"ez ( r ) = 0 , rr	(21)
1    / Ч               ЦЮ 7 ---e z ( r ) а + e ф ( r ) X--h r = 0, rc	(22)
e r ( r ) z - e z ( r ) + ЦЮ h ф = 0, c	(23)
e ф ( r ),           er ( r )     , ЦЮ — — + e m ( r ) - r-!^ • а + ^—hz = 0, ϕz r   rc	(24)
r ( ) + h ( ( r ) + ф а + X" hz ( r ) = 0, rr	(25)
T^ z (r) К- К ф (т) - ^^e r (r) = 0 ,	(26)
- h.T(r) x - /г 2 (т) + ^^е ф (г) = 0	(27)
» , (:)+ll f (r)+«+ ^« rc)=o ,	(28)

Плотность потока электромагнитной энергии – вектор Пойнтинга

5 = П Е ^х H ,                                 (28а)

где

П = с / 4 п .                                          (28в)

В цилиндрических координатах r , ф , z плотность потока электромагнитной энергии имеет три компоненты S_r , 5 _ф , S_z , направленные вдоль радиуса, по окружности, вдоль оси соответственно. Они определяются по формуле

I

[ Sr] №~Е Нф s=К = пк^Д

[ SzJ Мф^Н

или, с учетом предыдущих формул,

Sr = Ч^"^)™^

Sф = 'р'7!? ° -V'/' 1

Sz = n(erV'2 "e»kr c°2)

Предположим, что эти плотности потоков энергии удовлетворяют закону сохранения энергии, если

hr = ker

,

^ ф =^{- ke} ф .

hz =- kez.

Из (30, 34, 35) следует, что

^S r = n(^-e_v^ke z ^{+ ke} z ^e^^c °^ = ⁰ т.е. отсутствует радиальный поток энергии.

Из (31, 33, 15) следует, что

^ = ^ezkerc°2 + kerezsi2) = nkerez т.е. плотность потока энергии по окружности на данном радиусе не зависит от времени и других координат.

Из (32, 33, 34) следует, что

Sz = nkerkф^i2 + c°2) = 4ker\ т.е. плотность потока энергии по вертикали при данном радиусе не зависит от времени и других координат. Эти утверждения и были целью предположений (12-14).

Выполним замену переменных по (33-35) в уравнениях (21-28)

и перепишем их, не меняя нумерации:

er • e.n

+ e - фаа -xe = 0r r r z

-^a + evx-^^ker = 0

^{- e} z ^{+ e} r X ^{- k}^ _C ^^e ф = ⁰

e$ + e, -eTa-k^^e7 = 0

r ф r c z

ev          em

k-^ + ke - k-фа - kxe7 = 0 r r r z z

1 ^ez , 7 EW 4n - _n - k-^a + ^k^x - — ^e_r -—j_r = 0

,

, •     ,      . ew 4n. n kez-kerX + —%—Уф = 0

,

7 ^e

^eT । Eto 4П ■ _n

- k^ - ke_m + к—a + —e₇--/^ = 0

r Ф r C z C Jz

Можно заметить, что уравнения (41) и (45) совпадают и поэтому уравнение (45) можно удалить из системы уравнений.

Далее предположим, что продольная волна отсутствует, т.е ^^z   ^. Отсюда и из (18) следует, что ^ez   ^. Тогда система

уравнений (41-44, 46-48) принимает вид:

e„ • е,_

+ е - -^a = 0 r ^r r

,

• ^eфX^-S|■^ker =⁰

• ^erX ^{- k}^^Weф =⁰

е_Ф • e„

• —— + e--a = 0 r ^ф r

EW keфX--^er = 0

EW

^{- ke}rX + —^eф = ⁰

e,n             eT

- k^ - ke._n + k—a = 0 r ^ф r

.

В этой системе уравнений уравнения (44) и (48) совпадают. Следовательно, необходимо решить систему 6-ти уравнений (41-44, 46, 47) с 5-ю неизвестными ^er,eф,^’^a’^X^

Из (42, 46) находим

ЦЩ/ „ = EW c ^K — ck

или

k =±

Из (42, 50) находим

Доклады независимых авторов	2019 выпуск 45
е = ^кег =+ Ш&
ф СХ г - сх г.	(51)
Из (43, 47) также находим (49, 50), а из (43, 50) находим
е = Х^е =+ ^^е фк^ш г    ш^гц г.	(52)
Из (51, 52) находим шТШ _ Хс СХ    ШлУЕЦ	(53)
или Щл/ЕЙ =+1 сх - ,	(54)
шл/Ей х 1^ •	(55)
Из (52, 55) находим ег =- еф,	(56)

При (56) уравнения (41) и (44) совпадают и принимают вид:

ет фа + 1) + еФ = 0

.

Л, а по

Решение уравнения (57) имеет вид

еф = Лг(а + 1) ф                         , где А – некоторая константа. Таким образом, при данных

(58, 56, 50,33, 34) можно найти напряженности ^г'^ф'^"f ^ф как функции от ^Г"

Выше показано, что радиальный поток энергии равен нулю. При Zz из (35, 37) следует, что поток энергии по окружности также равен нулю. Из (35, 38, 56) найдем плотность продольного потока энергии

Sz = лкегАф =- Л^ег^еф = Пк2<;

Из (59, 58, 50) находим

_Sz = П^_Л2_г2(а + 1)

Найдем теперь поток энергии в цилиндрической волне радиуса ^, который равен мощности ^, переносимой этой волной:

P = J S^nrdr =

²™^^АЧт(²« ■ 3dT

или

_P = п^А²

(2 а + 4)^

R2a + 4

.

(61) найти P* R и

Таким образом, при данных А, а, R по (61) можно передаваемую мощность. С другой стороны, при данных напряженности ^Ф^^ из (61, 58) можно найти А, а и далее по (58, 56, 50,33, 34) найти все напряженности ^г> ^Ф*^т*^ф как функции от

Г.