Способ формирования вихревого поля СВЧ-диапазона

Вихревая пространственно-временная структура характерна для многих физических процессов. В настоящее время внимание исследователей, работающих в области лазерной физики и когерентной оптики, привлекли световые поля с винтовыми возмущениями волнового фронта. Такие возмущения обусловливают вихревой характер распространения световой энергии – оптические вихри. Данные физические явления успешно применяются для манипуляции микро- и нанообъектами, осуществления дальней связи, зондирования атмосферы и объектов [1, 2].

Электромагнитные волны терагерцового и СВЧ-диапазона по своим свойствам во многом схожи со световыми: так же характеризуются вектором Пойн-тинга и угловым моментом.

Существует ряд статей об успешном формировании вихревых полей терагерцового и СВЧ-диапазона [3–7]. В [3] описывается спиральная антенна, которая позволяет осуществить необходимую деформацию волнового фронта. Однако недостатком данного метода является невозможность получения значительной мощности вихревого поля. В работах [4–5] теоретически и экспериментально исследуется возможность формирования вихревого поля терагерцового диапазона на кремниевых элементах. Однако такие структуры сложны в изготовлении. В работе [6] рассматривается возможность формирования вихревого поля терагер-цового диапазона на кристалле ZnTe. Вместе с тем авторы статьи [6] отмечают сложность такой системы, работающей в широком диапазоне длин волн, из-за нелинейных свойств используемого кристалла. В работе [7] отмечается возможность формирования вихревого поля терагерцового диапазона на системе, использующей жидкокристаллическую структуру. Однако данный способ не позволяет получить значительную мощность вихревого поля.

Актуальной задачей является предложение простой структуры для формирования вихревого поля СВЧ-диапазона значительной мощности.

Целью работы является теоретический анализ возможности формирования вихревого поля СВЧ- диапазона на структуре, в виде неоднородности на торце круглого волновода.

1.    Теоретическая часть

В СВЧ-технике широко используются круглые волноводы. Наиболее интересным с физической точки зрения, в плане применения для формирования оптических вихрей, представляется тип волны Н01. Несомненным достоинством являются малые омические потери вследствие существования только радиальных токов в волноводе [8]. Однако существуют определенные трудности в возбуждении и обособлении данного типа колебания в волноводе. Электрические силовые линии волны Н01 в круглом волноводе представляют собой замкнутые окружности. Раскрыв круглого волновода с данным типом волны излучает в свободное пространство, то есть является простейшей антенной. Очевидно, данный способ не лишен недостатков. Однако на данном этапе анализируется сама возможность формирования вихревых полей с использованием круглого волновода.

При численном моделировании производится поиск полного распределения электромагнитных полей волновых уравнений методом конечных элементов [9]:

∇ ² × E + k ² E = 0,

∇2×H+k2H=0, где E – вектор напряжённости электрического поля; k – комплексное волновое число;

k =ω µε ;

ω – циклическая частота; ε – относительная диэлектрическая проницаемость; µ – относительная магнитная проницаемость; H – вектор напряжённости магнитного поля.

Граничные условия имеют вид [9]:

E T = Z s ( n × H T ),                                (2)

где E T – тангенциальная к границе раздела компонента вектора напряженности электрического поля; H T – тангенциальная к границе раздела компонента вектора напряжённости магнитного поля; Z s – импеданс на границе раздела; n – единичный вектор нормали к поверхности.

Вектор напряженности электрического поля, внешний к рассматриваемой поверхности, задается уравнением [9]:

E - J ( E t xV G + E n xV G )d S , (3)

S где S – поверхность, через которую излучается электромагнитная энергия; EN – нормальная к поверхности компонента вектора напряжённости электрического поля; G – функция Грина.

При моделировании пространство разбивается на тетраэдры, в вершинах которых рассчитываются значения электрического и магнитного полей [9]. Для установления факта наличия вихревого поля в СВЧ-диапазоне удобно использовать диаграммы направ- ленности, подобно как для антенной техники. Они позволяют получить полную картину распределения поля в пространстве.

2.    Результаты моделирования

В результате численного моделирования процесса излучения из круглого волновода (материал стенок волновода – серебро, толщина стенок – 1 мм, заполнение – воздух) радиусом 19,3 мм на частоте 10 ГГц построены диаграммы направленности, которые отображают модуль напряжённости электрического поля в зависимости от углов сферической системы координат в ближней (20 мм) и дальней зонах, представленные на рис. 1 и рис. 2 соответственно.

|E|. B/m 3.1282e+003 2.9329e+003 2.7377e+003 2.5424e+003 2.3472e+003 2.1519e+003 1.9566e+003 1.7614e+003 1.5661e+003 1.3709e+003 1.1756e+003 9.8039e+002 7.8514e+002 5.8989e+002 3.9463e+002 1.9938e+002 4.1305e+000

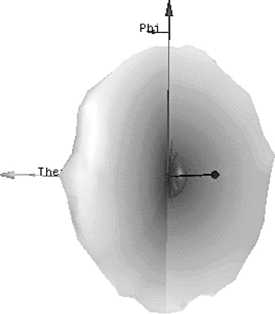
Рис. 1. Диаграмма направленности круглого волновода в ближней зоне

|E|, B/m 1.0324e+001 9.6826e+000 9.0413e+000 8.4001e+000 7.75896+000 7.1176e+000 6.4764e+000 5.83516+000 5.19396+000 4.5527e+000 3.91146+000 3.27026+000 2.6290e+000 1.9877e+000 1.3465e+000 7.05266-001 6.4026e-002

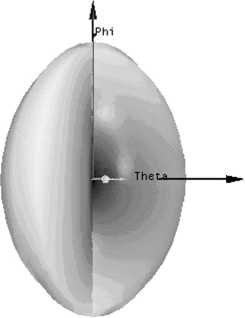
Рис. 2. Диаграмма направленности круглого волновода в дальней зоне

Как видно из графиков (рис. 1, 2), вихревое излучение волны типа Н01 из открытого торца круглого волновода на является вихревым. Требуется введение неоднородности с целью получения сдвига фаз волн, прошедших через неоднородность и свободное пространство без искажений. В качестве неоднородности может выступать диэлектрик с относительной диэлектрической проницаемостью £ > 1. В ходе численных экспериментов были подобраны минимальные размеры неоднородности из слюды с £ = 5,5 (выбранной по причине возможности её работы при больших мощностях электромагнитного поля) на торце круглого волновода, формирующей вихревое поле СВЧ. Неоднородность выполнена в виде половины конуса радиусом 19,3 мм и высотой 1 мм (рис. 3).

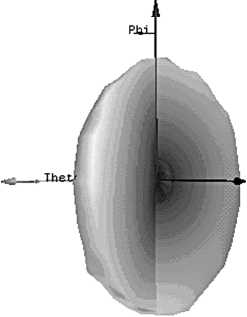
Данная неоднородность позволяет сдвинуть фазу вектора электрического поля и внести винтовую дислокацию в структуру поля. Численное моделирование круглого волновода с радиусом 19,3 мм с половиной конуса из диэлектрика с £ = 5,5 на торце, частота 10 ГГц, позволяет построить следующие диаграммы направленности в ближней (20 мм) и дальней зонах (рис. 4, 5). Таким диэлектриком может быть слюда, имеющая низкий тангенс угла диэлектрических потерь и указанную относительную диэлектрическую проницаемость. Технология изготовления такого половинного конуса из слюды включает следующие операции: формирование целого конуса и разлом его на две части. Такая технология оказывается более экономически выгодной по сравнению с технологией изготовления кремниевых элементов, для которых дополнительно требуются ресурсоёмкие процедуры

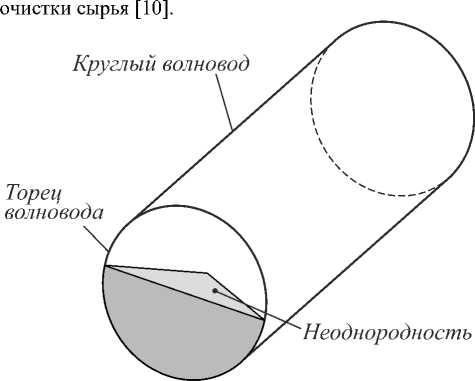
Рис. 3. Неоднородность на торце круглого волновода

Как видно из диаграмм (рис. 4, 5), круглый волновод с неоднородностью на торце позволяет сформировать вихревое поле в дальней зоне. Диаграмма (рис. 5) представляет собой спираль, что подтверждает наличие вихревого поля. Фаза электрического поля изменяется не только во времени, но и в пространстве.

|E|, Mz

2.7128е+003 2.5447е+003 2.3765е+003 2.2084е+003 2.0403е+003 1.8721е+003 1.7040е+003 1.5358е+003 1.3677е+003 1.1995е+003 1.0314е+003 8.6325е+002 6.95116+002 5.2697е+002 3.5883е+002 1.9068е+002

2.2540е+001

|Е|, В/м

1.0508е+001 9.8586е+000 9.2089е+000 8.55936+000 7.90976+000 7.26016+000 6.6104е+000 5.9608е+000 5.3112е+000 4.6616е+000 4.01196+000 3.3623е+000 2.7127е+000 2.06316+000 1.4134е+000

7.63816-001 1.1419е-001

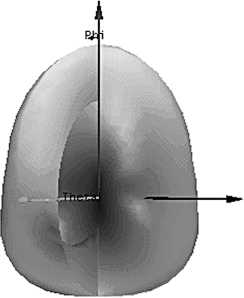
Рис. 4. Диаграмма направленности круглого волновода с неоднородностью на торце в ближней зоне

Заключение

Проведённое численное моделирование подтверждает возможность формирования вихревого поля СВЧ-диапазона с помощью предложенной структуры в виде неоднородности на торце круглого волновода. В результате расчётов установлено распределение электрического поля в ближней и дальней зонах для предложенной структуры. В дальнейшем планируется провести дополнительную оптимизацию согласования волновых сопротивлений круглого волновода и свободного пространства, установить оптимальные геометрические соотношения конструктивных элементов, оценить энергию вихревого поля для СВЧ- и терагерцового диапазонов.