Способ формообразования тонкостенных осесимметричных деталей усеченной сужающейся формы на основе процесса отбортовки

1 – плита верхняя; 2 – раздвижные сектора; 3 – эластичный элемент; 4– заготовка; 5 – конус; 6– опорное кольцо; 7– плита нижняя; 8 – матрица; 9 – деталь

PdP + Tp - Тв (1 + f • ctg«Mamp ) = 0 , (1)

где T p - напряжения в меридиональном направлении;

Т_в - напряжения в тангенциальном направлении;

f – контактное трение заготовки, коэффи- циент трения;

^ _матр - угол конусности матрицы.

Используем условие пластичности для трансверсальной анизотропии:

тв = kTS = TS ,           (2)

где T S - напряжение текучести;

к - коэффициент, равный к = 21. 1 —— д [2];

Д - коэффициент анизотропии трансверсально-изотропного тела.

Решение (1) и (2) имеет вид:

^О р ^{— O} S ( 1 ⁺ f ' ctg « Mamp ) f ¹ - — 1 ,  (3)

V ^р 7

где r_дет – меньший радиус конической детали; р - текущий радиус детали.

При р = г дет ; У_р =0. Анализ выражения (3) показывает, что напряжения У_р растет с увеличением р . Этому должно способствовать утонению заготовки для элементов, примыкающих к больше диаметру и уменьшению размера внутреннего диаметра кольцевого выступа.

Технологически возможную толщину получим из уравнения связи напряжений и деформаций:

Т_Т = 5 заг

^{1 -( 1 - д )} '

^О р ! °_в + 1

Р^ - 1

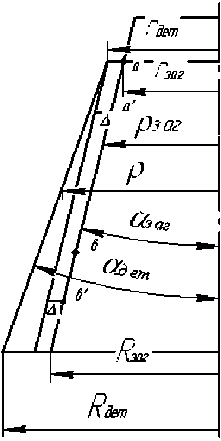
Рис. 2. Схема процесса

^{1 -} Д'^ р / ° 9 V р

. (4)

Чтобы значения S_Т имели постоянное значение необходимо выполнить условие минимизации [3]:

где А —---. Таким образом, ---= — с +1, rdem                   1-А

отсюда:

R дет

А.

дет

- S T ) ² d р ^ min ,

с —

1 -А

- l

.

Подставим (9) в (6) и получим:

где S д _ет – заданная толщина детали;

S_Т – технологически возможная толщина, которая получается после формообразования заготовки;

r д _ет – меньший радиус детали;

р

—= +

1 -А

l ( р - 1 ) .

Зная l и с можно найти наименьший и наибольший радиусы заготовки, используя (10):

R

дет

R дет

r дет

больший относительный

р

заг

р

радиус детали.

Варьируемыми параметрами возьмем радиус заготовки р _заг , который примем в виде линейной зависимости:

, '+ ^{1 р} - ^{1 )}

1 -А

р

^— с ^{+ 1 р} .             (6)

р заг

Из двух неизвестных коэффициентов, с определим из условия, что при р — г дет (см. рис. 2):

^р заг ^— r dem ^-А •            ⁽⁷⁾

r д _ет – меньший радиус детали; R д _ет – больший радиус детали; р - текущий радиус детали; р _заг — радиус заготовки; г_заг - меньший радиус заготовки; R_3ar - больший радиус заготовки; А -горизонтальное перемещение элементов заготовки при деформировании на 1 стадии, принятое для всех элементов одинаковым; М _заг - угол конусности заготовки; О дет - угол конусности детали

В относительных единицах при р =1:

р заг — 1 -А .              (8)

Коэффициент l позволяет определить радиус наибольший заготовки, который дает возможность получить деталь с минимальной разнотол-щинностью.

Выражение (5) примет вид с учетом безраз-

= мерных величин 5 дет

Rдет

S дет

Sзаг

,

г. - дет

— r дет

, дет

r дет

R dem I

J 3 S дет

1 I

R^дет , т.е. от 1 до R дет :

—

.   . У / у + 1

1 - ( 1 - д )— —1-1= + 1 ( р - 1 ) - 1

_          ^1- Д ' О-р / 09 1 1 -А           .

■ dр ^ min .

Минимизацию выражения (5) проведем путем варьирования коэффициента l :

д дl

Rдет j j 5 дет -1-(1 - Р) b +        +(1-д)Ь| (р-1Н (р —1)dр — 0 .(12)

1 I                          ( 1 ^-А )                      J

где

b _— b 1 ⁺ b 2

b₁ =1 при р =1;

^PI^e =0;(14)

(1 + f ■ ctgttMamp 11 - =^j + 1       __ b2 =--------------V <дет ^ ^ при P = RДет, (15)

1 - А (1 + f " с^«матр 1 1 - =

\    R Дет V

P р

,         заг – соответственно от- р          , заг rдет           дет носительные радиусы детали и заготовки.

Или

S Дет - 1 - b ( 1 - ц ) +“Т--

( 1 -a )

x

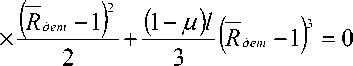
отсюда

1 + (1 - Ц )b - S Дет - ---Hv b i=з—r   ; ^ . (16)

2 ( R Дет - 1 ) (1 - Ц)Ь

Чтобы вычислить l следует найти соотношение между a И S Дет ; при P = Г_Дет или р =1. Из (4) имеем, приравняв S_Дет = S T и приняв соотношения:

Г - Г = А или 1 — Г заг = А или.

Дет заг                   ^заг             Г заг — 1 А

Тогда

S Дет - 1 =- ( 1 - Ц ) ⁽ - "  заг ' =- ( 1 - ц )^= ,

Г заг1

Отсюда А = —^^^Ает--.(17)

2 - S Дет - Ц

Для наглядности проанализируем аналитические закономерности с помощью построенных графиков (рис. 3 – 12).

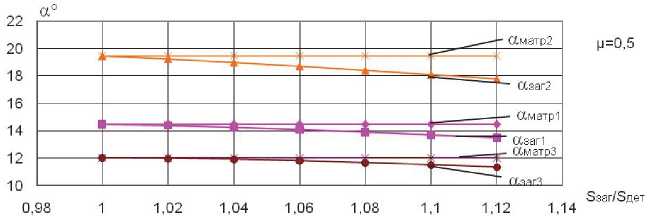
Рис. 3. Зависимость отношения S I S Дет от угла конусности заготовки И _заг при ц = 0,5 ; f = 0,1 и различных значениях угла конусности матрицы:

0  00

^ матр 1       , ^; ^ матр 2       , ^; ^ матр 3

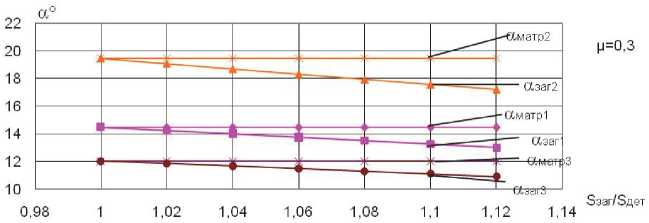
Рис. 4. Зависимость отношения S_заг I S д _ет от угла конусности заготовки « _заг при ц = 0,3 ; f = 0,1 и различных значениях угла конусности матрицы: И матр 1 = 14,5 0 ; И матр 2 = 19,5 0 ;

^ матр 3 = ¹²

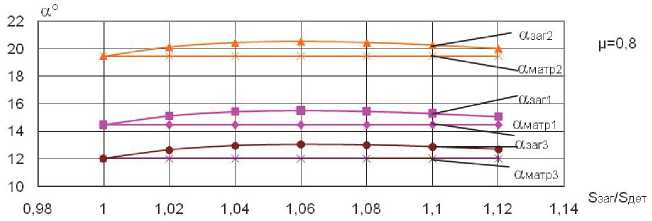
Рис. 5. Зависимость отношения S_заг I S д _ет от угла конусности заготовки И _заг при ц = 0,8 ; f = 0,1 и различных значениях угла конусности матрицы: ^И матр 1 = ¹⁴,^{5 ; И} матр 2 = ¹⁹,^{5 ; И} матр 3 = ¹²

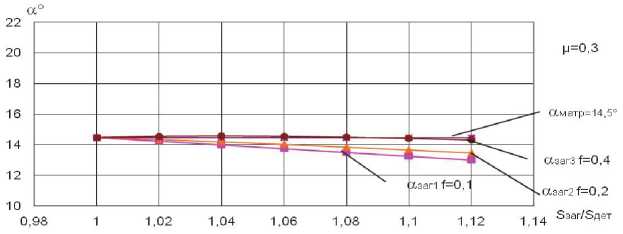
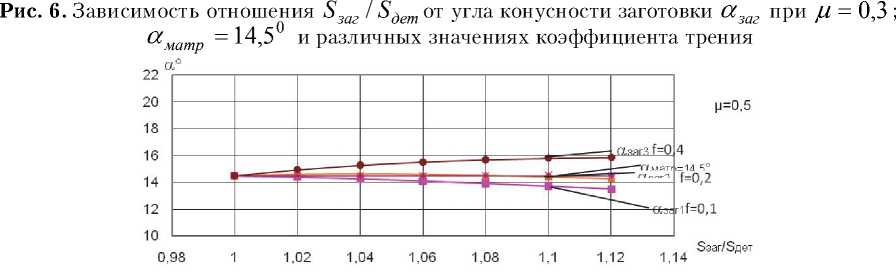
Рис. 7. Зависимость отношения 5* заг / S g _em от угла конусности заготовки « заг при Ц = ^0,5 ; « матр = 1^4,5 0 и различных значениях коэффициента трения

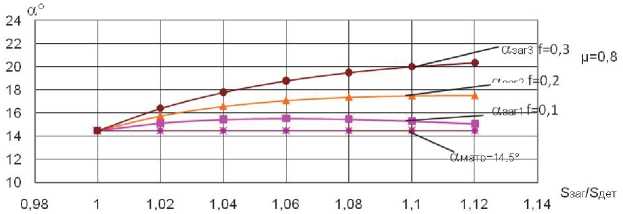
Рис. 8. Зависимость отношения S / 5 д _ет от угла конусности заготовки « _заг при Ц = ^0,8 ; « матр = ^14,5 и различных значениях коэффициента трения

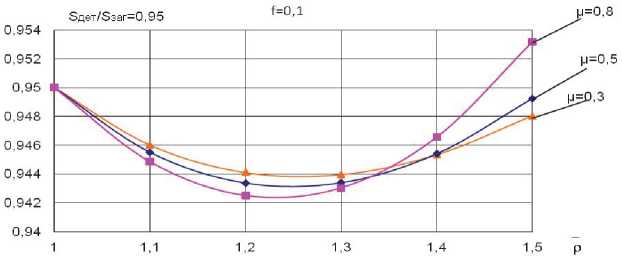
Рис. 9. Зависимость отношения S t / S заг по заданному соотношению S дет / S заг = 0,95 ; f = 0,1 ; « матр = 14,5 0 ; R дет = 1,5 и различных значениях коэффициента анизотропии

Ц = 0,3 ; Ц = 0,5 ; Ц = 0,8

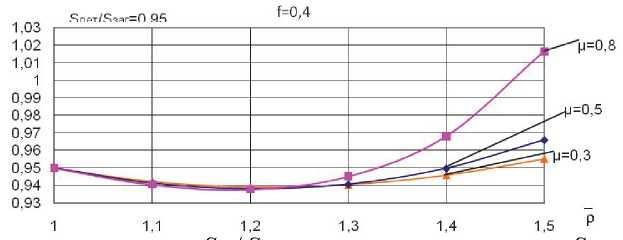
f=0,4

Дп^т/ДчЯГ^П QS

0,99 0,98 0,97 0.96 0.95 0.94 0.93

1.03

1,02

1,01

Рис. 10. Зависимость отношения S t / S_заг по заданному соотношению S дет / S_заг = 0,95 ; ^f = 0,4 ^; R Дет = ^{1,5 ;} « матр = ¹⁴, 5 ⁰ и различных значениях коэффициента анизотропии ^{ет , матр} Ц= 0,3 ; Ц= 0,5 ; Ц= 0,8

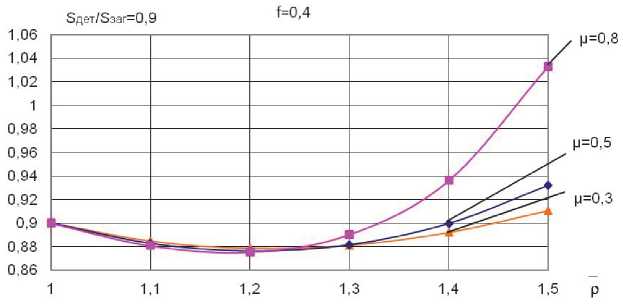
Рис. 11. Зависимость отношения S_T / S заг по заданному соотношению S дет / S заг = 0,9 ; f = 0,4 ; R дет = 1,5 ; И матр = 14,5 0 и различных значениях коэффициента анизотропии Ц = 0,3 ;

Ц = 0,5 ; Ц = 0,8

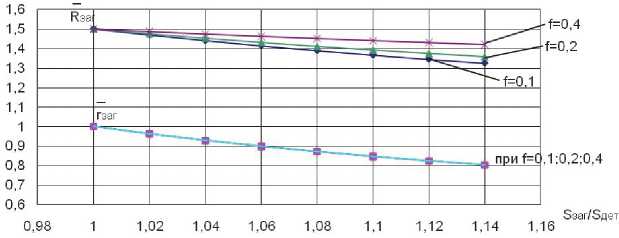
Рис. 12. Зависимо с ть отношения большого и малого относительного радиуса заготовки от ^S заг / ^S Дет при R Дет = 1,5 ; ^И матр = ^ и

Задаваясь соотношением S д _ет / S_заг и раз личными значениями коэффициента анизотро

-

-

пии, коэффициента трения, используя формулы (13, 14, 15, 16, 9, 11, 4) построим зависимость отношения S_Т / S_заг .

По проведенной работе можно сделать выводы: . При уменьшении коэффициента анизотропии Ц сокращается разница между углами И матр

различных значениях коэффициента трения от заданной толщины при малых Ц составляет 1%.

. При значительных значениях коэффициента

и И заг , что особенно сильно сказывается при малых значениях угла конусности матрицы И матр .

. С возрастанием коэффициента трения раз

-

ница между значениями больших радиусов R д _ет и R_заг уменьшается и с возрастанием значений коэффициента анизотропии Ц эта разница прак-

анизотропии, близких к единице, угол конусности заготовки может быть больше угла конусности детали.

Таким образом, с точки зрения получения наименьшей разнотолщинности детали способ эффективен для случая, когда имеет место наименьших значений коэффициента анизотропии Ц и коэффициента трения f .

Работа проводилась при финансовой поддержке Министерства образования и науки Российской Федерации.