Способ изучения разнообразия орнитофауны методом вейвлет-анализа

Птицы играют важную роль в различных экосистемах. Информация об их видовом составе и численности представляет интерес для специалистов из различных областей. Учет, особенно ночных, птиц затруднен. Было установлено, что звуковые сигналы несут много ценной информации. По голосам птиц можно судить об их видовом составе, численности и миграциях [1]. Для распознавания сигналов со сложными спектральными характеристиками широко применяется метод вейвлет-анализа [2]. В связи с этим возникла идея проверить возможность распознавания голосов птиц методом вейвлет-анализа. Целью предлагаемой работы является математическая проработка процесса распознавания голосов птиц и разработка программного обеспечения, предназначенного для распознавания голосов птиц в режиме постпроцессинга.

МАТЕРИАЛ И МЕТОДЫ

В исследовании использовалась выборка из 269 голосов птиц. Выборка включала в себя голоса 166 видов птиц России, представленных от 1 до 14 вариантами. Варианты являлись разными трелями птиц одного вида, например, пение или беспокойство. Исходные звуковые файлы предварительно были преобразованы в единый звуковой формат: частота дискретизации 5512 Гц, разрядность 8 бит, моно, импульсно-кодовая модуляция. Далее, проводилось создание вейвлетов. Вейвлет – это некая функция, заданная таблично (небольшой массив чисел), определенным образом характеризующая сигнал [2]. Среди этих функций важную роль играют ортогональные вейвлеты. У такого вейвлета коэффициент корреляции с целевым сигналом стремится к единице, в то время как по отношению к другим сигналам корреляция этого вейвлета стремится к нулю [3].

Для создания вейвлета необходимо избавиться от избыточности исходного сигнала и выявить характерную область, адекватно описывающую этот сигнал. Устранение избыточности сигнала произ-

водится с помощью процедуры детектирования. Степень разреженности исходного сигнала задается размером так называемой рамки детектирования. Выбранная область детектированного сигнала подвергается процедуре нормирования. Нормированный участок детектированного сигнала и является вейвлетом [4]. Нормирование позволяет устранить влияние амплитуды сигнала на процесс распознавания.

Важно определить оптимальную длину вейвлета. Длинные вейвлеты более информативны, но могут давать ошибочную корреляцию с нецелевыми сигналами. Создав хорошие (ортогональные) вейвлеты, мы можем использовать их в дальнейшем для распознавания неизвестных сигналов [5].

В ходе экспериментов было установлено, что оптимальной длиной вейвлета является 70 отсчетов, оптимальный размер рамки детектирования – 100 отсчетов.

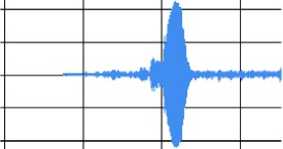
Рассмотрим процедуру создания вейвлета на примере голоса выпи большой. Вначале необходимо считать исходный звуковой сигнал и записать его в массив (рис. 1).

0,61-------------------------------------

0,4

0,2

О

-0,2

-0,4

-0,6-----

• -0,8-----

  -1-----

• -1,2-1------------------------

  0     50000   100000 150000

Рис. 1. Исходный массив голоса выпи большой

После этого требуется избавиться от избыточности сигнала. Для этого осуществляется процедура детектирования сигнала. Предположим, исходный сигнал записан в массив Ai, i изменяется от 1 до N. Задается рамка считывания сигнала. Малый размер рамки повышает информативность, но оборачивается большими накладными расходами в плане производительности. Как уже говорилось выше, размер рамки был определен в 100 единиц. После этого весь диапазон массива A делится на N/100 рамок. Внутри каждой рамки находили сумму квадратов - " ■ - =- ■ , где j - номер рамки, а i - индекс элемента массива а внутри j-й рамки. Далее, получали массив детектированного сигнала Bj , где элементы массива B вычисляются по фор муле: ■ - - -. На рис. 2 показан детектированный сигнал голоса выпи большой. Видно, что размер его массива в сто раз меньше исходного.

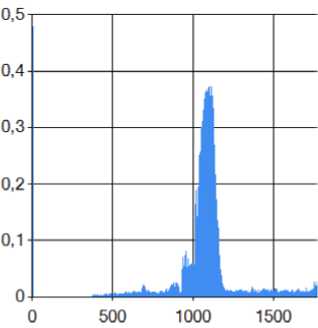
Рис. 2. Детектированный сигнал голоса выпи большой

Произведя детектирование сигнала, выбираем область, характерную для конкретного сигнала. Мы остановились на длине вейвлета в 70 отсчетов.

Выбрав характерную область детектированного сигнала Bj , где j изменяется от B_min до Bmax ( m = B_max - B_min ), осуществляем нормирование детектированного сигнала Bj на отрезке от B_min до B_max . Нормирование проводили следующим образом. Вначале находим среднее арифметическое

=        3 , сумму квадратов отклонений sum                                  ।---~ и дисперсию '    ■ .

Зная ■■ и у, можно найти вейвлет, являющийся мас-

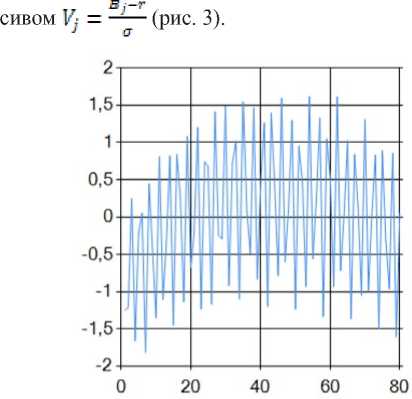
Рис. 3. Вейвлет голоса выпи большой

Процесс распознавания проходил следующим образом. На вход системы подается неизвестный сигнал Ui. Далее, производится детектирование сигнала с такой же рамкой (в нашем случае 100 отсчетов), что и при создании вейвлета. Получаем массив детектированного сигнала Cj (в сто раз меньше отсчетов, чем в исходном сигнале). Далее выбирается шаг распознавания myStep, равный размеру вейвлета m (в нашем случае m=70). Внутри шага распознавания определяется коэффициент корреляции участка исследуемого сигнала Cj, равного myStep, со сравниваемым вейвлетом. Определение коэффициента корреляции CORj проводили следующим образом. На исследуемом участке находим среднее арифметическое r и дисперсию о способом, используемым при создании вейвлета. На основании r и о нормировали выбранный уча- сток исследуемого детектированного сигнала, получая массив Dj. Имея нормированный детектированный сигнал Dj и вейвлет Vj, находим коэффициент корреляции CORj.

^j+mystep Q_xy

COR; =

myStep

Найдя коэффициент корреляции на выбранном шаге, сдвигаем рамку распознавания на один элемент и возобновляем процесс (рис. 4).

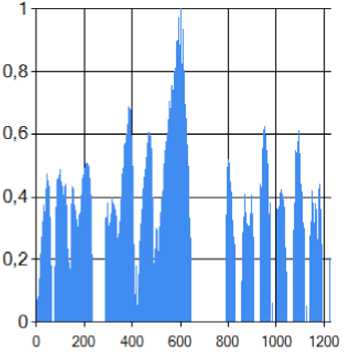
Рис. 4. Корреляционная функция между голосом выпи большой и вейвлетом выпи большой

Если коэффициент корреляции неизвестного сигнала и известного вейвлета близок к единице, программа принимает решение об успехе распознавания.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Испытания программного обеспечения, разработанного в соответствии с вышеприведенными рекомендациями выявили некоторые проблемы. Так, все вейвлеты давали коэффициент корреляции, равный единице к целевому сигналу. Однако, чем больше использовалось сигналов, тем труднее было разработать вейвлеты, дающие низкие коэффициенты корреляции по отношению ко всем остальным сигналам (менее 0,65). Эта работа очень усложнялась, когда сигналов становилось больше десяти. Была построена корреляционная матрица, включающая в себя коэффициенты корреляции между 269 сигналами и 269 вейвлетами. К сожалению, результаты оказались неоднозначными – часть вейв-

Таблица. Степень ортогональности различных вейвлетов летов обладала высокой степенью ортогональности. Например, вейвлет сороки дал низкий коэффициент корреляции для 72 сигналов, вейвлет лугового луня – дал низкую корреляцию для 37-ми голосов птиц (табл.).

Вейвлет	Количество случаев относительно низкого коэффициента корреляции к звуковым сигналам (r<0,65)
Сорока_1	72
Луговой лунь	37
Камышовка-барсучок	35
Вертишейка	30
Пеночка-трещотка	19
Белый аист	17
Чика	17
Канарейка	9
Большой пестрый дятел	7
Глухарь_3	5
Горлица обыкновенная	3
Ворон_1	2
Кенарь	2
Соловей_2	2
Большая синица_2	1
Дятел_2	1
Козодой_2	1
Крапивник_1	1
Пустельга_2	1
Садовая камышовка	1
Сова полярная	1
Сова ястребиная	1
Соловей_5	1
Соловей_13	1
Сплюшка	1
Широконоска	1

Стало очевидно, что надежному распознаванию всех голосов птиц мешают вейвлеты с высокой степенью ортогональности. Для решения этой проблемы было решено перейти к частичной ортогональности вейвлетов, используя при распознавании голосов птиц, эвристики, полученные при анализе корреляционной матрицы. Предлагается следующая стратегия.

Пример эвристики: так как коэффициент корреляции неизвестного сигнала с вейвлетом клуши превышает 0,99 и равен 0,62±0,05 для вейвлета большой синицы_1, то исследуемый сигнал является голосом клуши.

• 1.    Сравнивается первый звуковой сигнал со всеми вейвлетами, находится вейвлет с минимальным коэффициентом корреляции, результат заносится в таблицу. Например, для голоса балабана

• 2.    Удаляется ранее использованный вейвлет (лесного конька) из числа вейвлетов, участвующих в распознавании (в нашем случае, после этого остается 268 вейвлетов).

• 3.    Берется новый звуковой файл (Бекас) и снова строится вейвлет из числа имеющихся 268 экземпляров, дающих минимальный к нему коэффициент корреляции (в нашем случае это – вейвлет вертишейки с r=0,59).

• 4.    Удаляется вейвлет вертишейки из числа вейвлетов, участвующих в распознавании.

• 5.    Повторяются этапы с первого по четвертый до последнего звукового сигнала.

минимальную корреляцию из всех вейвлетов дал вейвлет лесного конька (r=0,42).

Важным моментом здесь является то, что классифицирующим множеством являются сами вейв- леты. Так как мы постепенно отбрасываем наиболее ортогональные вейвлеты, постепенно накапливаются вейвлеты с высокими коэффициентами корреляции. Для решения этой проблемы можно расширить классифицирующее множество. Предположим, мы хотим создать систему распознавания голосов ста видов птиц России. Для повышения надежности распознавания можно классифицирующее множество расширить за счет вейвлетов, например тропических птиц или даже вейвлетов звуков автомобилей. То есть, сто звуков российских птиц будут сравниваться с двумястами-тремястами вейвлетами.

Разработанное программное обеспечение позволяет классифицировать различные трели птиц од- ного вида. Распознаются 166 видов России с надежностью 0,87. Удается распознать различные трели птиц одного вида.