Способ обеспечения навигационной безопасности для автономного необитаемого подводного аппарата

Цитирование: Шостак С. В. Способ обеспечения навигационной безопасности для автономного необитаемого подводного аппарата / С. В. Шостак, А. В. Бенгард, Г. В. Дорофеев, П. А. Стародубцев // Журн. Сиб. федер. ун-та. Техника и технологии, 2024, 17(6). С. 814–821. EDN: RBLONU

Активное освоение Мирового океана вызвало бурное развитие технологий в области исследования подводного пространства. Наиболее перспективным средством изучения Мирового океана служат необитаемые подводные аппараты (НПА), когда человек отсутствует на борту аппарата. Главным преимуществом НПА является возможность работы в сложной окружающей обстановке с минимальным участием человека. Наиболее востребовано применение НПА на больших глубинах, а также в покрытых льдом районах [1, 2, 3].

В настоящее время известны три типа НПА: буксируемые, самоходные, управляемые по кабелю, и автономные самоходные. Наиболее примечательный тип – автономные самоходные НПА. Указанный тип НПА является автономным необитаемым подводным аппаратом (АНПА). Такие аппараты используются в качестве информационных средств для решения различных исследовательских задач освоения Мирового океана и подледных исследований [1, 2].

Для решения поставленных задач АНПА принципиально необходимо навигационное обеспечение работ. В настоящее время для этого используются активные гидролокаторы. Такой – 815 – гидролокатор излучает звуковые сигналы в заданном направлении и принимает отраженное эхо. По скорости получения ответной реакции от сканируемого объекта вычисляется расстояние до него. Для совершения подобных операций гидролокатор оснащается специальным излучателем, приемной антенной и приемником. При этом излучатель гидролокатора свободно вращается в необходимом направлении [3].

Рассмотрим другой способ локализации объектов в пространстве, когда формируется веер характеристик направленности в приемной антенне, что позволяет одновременно «освещать» пространство в широком секторе углов.

В качестве приемной антенны и для упрощения выкладок будем рассматривать линейную антенную решетку (АР), состоящую из M преобразователей. Геометрия линейной эквидистантной антенной решетки и падающей волны с плоским фронтом представлена на рис. 1.

В результате в АР формируется пространственно-временной сигнал (ПВС) вида

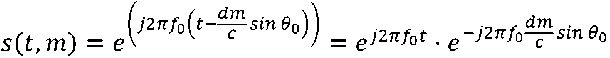
= ej2^fot . e-j^dmSine0'

В выражении (1) f ₀ – центральная частота гармонического сигнала, t – время, λ ₀ – длина волны сигнала, d – расстояние между преобразователями, θ ₀ – угол падения волны.

Так как обработка сигнала проводится, как правило, в дискретном виде и, учитывая, что d = 0,5 λ 0 , выражение (1) преобразуется

s(n,m) = e^}^^k°ⁿ ■ _e-)™sme_Oi                                      (2)

где k ₀ – номер отсчета частоты для центральной частоты f ₀; n = (0 ÷ N – 1) – отсчеты в области времени; N – число отсчетов.

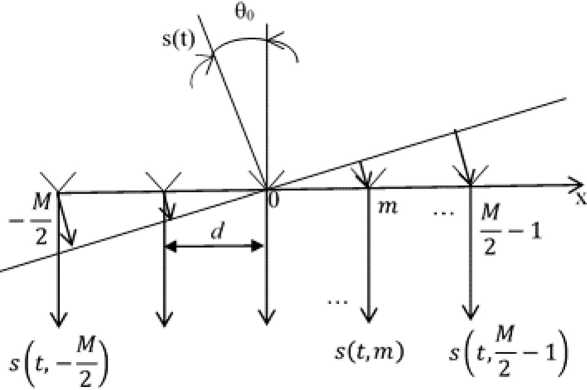
Рис. 1. Модель формирования пространственно-временного сигнала на антенной решетке: s ( t ) – приходящий сигнал, θ 0 – направление на источник сигнала, s ( t , m ) – сигнал в канале m , m – номер преобразователя антенной решетки, M – число преобразователей антенной решетки, d – расстояние между элементами решетки

• Fig. 1.    Model of the formation of a spatiotemporal signal on the antenna array: s(t) is the incoming signal, θ ₀ is the direction to the signal source, s(t, m) is the signal in channel m, m is the number of the antenna array converter, M is the number of antenna array converters, d is the distance between the elements grids

Как видно из (1) и (2), ПВС факторизуется, т.е. представляется произведением временной и пространственной составляющих. Это позволяет проводить обработку раздельно как по временной, так и по пространственной координатам.

Получим двухмерный спектр Фурье выражения (2) [4]:

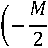
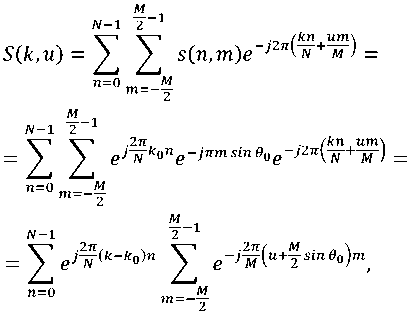
М \

--1) , u – пространственная частота.

В выражении (3) первая сумма определяет частотный спектр сигнала (2), вторая определя- м ет пространственный спектр. При условии k = k0 и и = - —sin 0О выражение (3) имеет максимальное значение

S^k,^ ^N-M.

Для раздельного наблюдения целей, находящихся на разных пеленгах, необходимо оценить разрешающую способность [5, 6]. Разрешающая способность по пеленгу определяется ортогональностью пространственных гармоник. Получим условия ортогональности для двух близкорасположенных по пеленгу целей, для чего найдем скалярное произведение двух гармоник e –π m sinθ ₁ и e –π m sinθ ₂

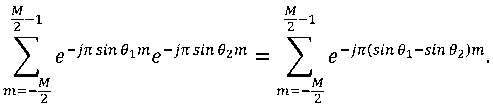
Несложно показать, что (5) – это сумма геометрической прогрессии, модуль которой равен

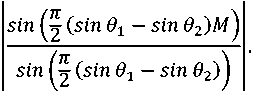
Отсюда следует, что две пространственные гармоники ортогональны, если выполняется условие

sin 0, - sin вт = + —. M

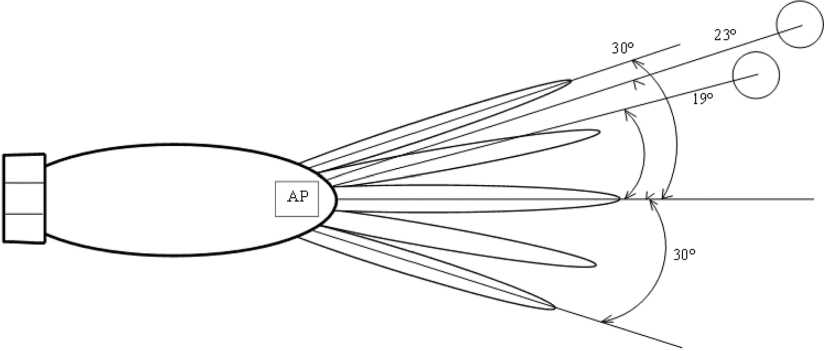
Рис. 2. Подводный аппарат и обнаружение им малоразмерного объекта

• Fig. 2.    Underwater vehicle and its detection of a small object

Предполагается, что на АНПА длиной в 3 м при рабочей частоте f ₀ = 200 кГц можно разместить 80 элементов с общей длиной антенны 30 см. При этом максимальная дальность будет составлять 300 м [7].

Для проверки работоспособности вышеизложенного способа проведем моделирование в среде MATLAB [8]. Возьмем в качестве примера подводный аппарат, имеющий на борту 32 преобразователя и излучающий сигнал с длительностью в 128 отсчетов. Предполагается, что подводные объекты находятся на пеленгах 19° и 23° соответственно. На рис. 3–6 представлены спектры ПВС в трехмерном виде при различных отношениях сигнал/шум: при отсутствии помех, 3дБ, –10 дБ и –15 дБ, а на рис. 7 – двухмерные изображения спектров ПВС при тех же отношениях сигнал/шум.

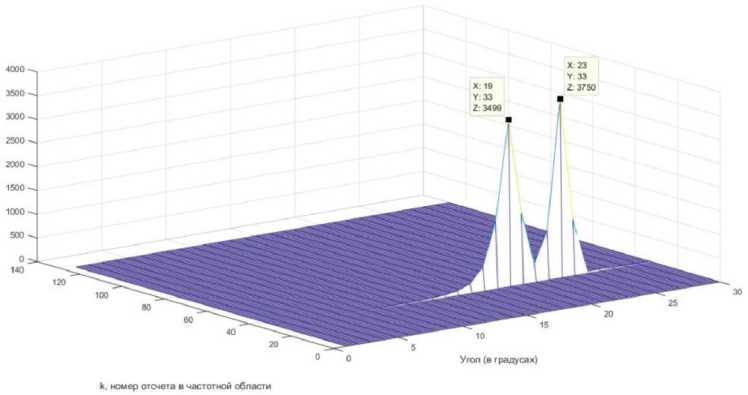
Рис. 3. Спектр ПВС в трехмерном виде при отсутствии помех

Fig. 3. The PVS spectrum in three-dimensional form in the absence of interference

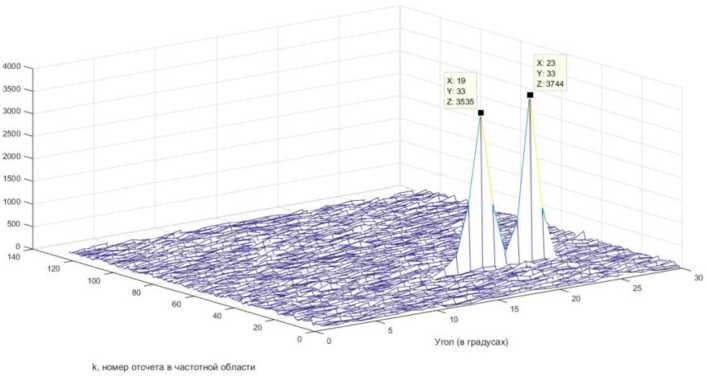
Рис. 4. Спектр ПВС в трехмерном виде при отношении сигнал/шум S/N = 3 дБ

Fig. 4. The PVS spectrum in three-dimensional form with a signal-to-noise ratio S/N = 3 dB

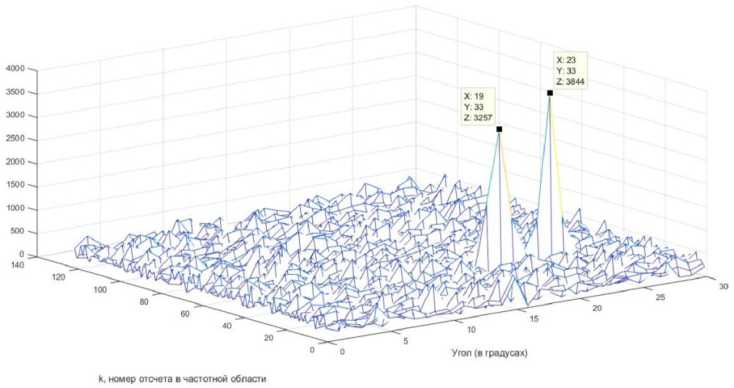
Рис. 5. Спектр ПВС в трехмерном виде при отношении сигнал/шум S/N = –10 дБ

Fig. 5. The PVS spectrum in three-dimensional form with a signal-to-noise ratio S/N = –10 dB

Как можно заметить на рис. 3–7, положение подводного объекта по пеленгу можно оценить даже при относительно низких уровнях отношения сигнал/шум. Особенно это заметно на рис. 7.

В представленных материалах рассмотрен способ обнаружения целей и оценка их координат для АПА. Задача решается на основе обработки ПВС. В работе представлена модель формирования ПВС. Показано, что для простого гармонического сигнала ПВС разлагается в произведение временной и пространственной составляющих. Это делает возможным проводить двухмерное спектральное разложение ПВС. Разложение проводится на основе алгоритма быстрого преобразования Фурье (БПФ), что позволяет формировать в приемной антенне веер характеристик направленности и одновременно обнаруживать подводные цели на различных на-

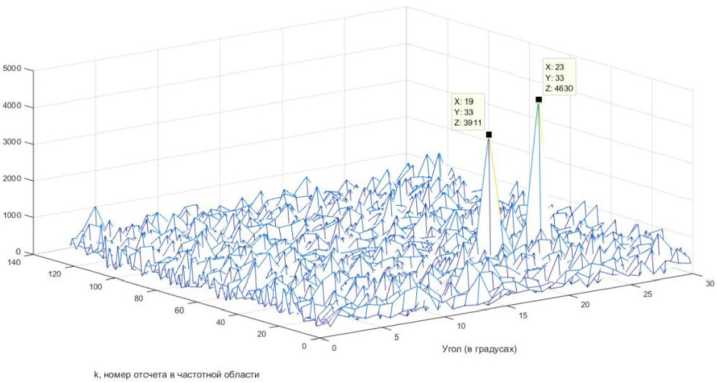
Рис. 6. Спектр ПВС в трехмерном виде при отношении сигнал/шум S/N = –15 дБ

Fig. 6. The PVS spectrum in three-dimensional form with a signal-to-noise ratio S/N = –15 dB

Рис. 7. Двухмерное изображение спектров при различных отношениях сигнал/шум

Fig. 7. Two-dimensional image of spectra at different signal-to-noise ratios правлениях с оценкой их пеленгов. Дальность до целей оценивается по задержке эхо-сигналов относительно зондирующего. В работе показано, что фактически программными средствами возможна многоканальная параллельная обработка ПВС. Работоспособность представленного способа проверена моделированием в пакете MATLAB.