Способ обнаружения отказов при экономичном резервировании бортового оборудования беспилотного летательного аппарата

Наиболее просто реализуем способ обнаружения мгновенных отказов, основанный на контроле по пороговой величине. В [2-5] описаны устройства обнаружения отказов, управления и восстановления работоспособности резервированных систем с использованием контроля по пороговой величине. Данные устройства позволяют непрерывно функционировать двухканальной системе при следующих отказах в одном из каналов: скачки выходных параметров вверх (типа короткого замыкания) или вниз (типа обрыв соединения), а также плавное изменение до максимального или минимального значения, возможного в данной системе. Принципиальным недостатком способа контроля по пороговой величине выступает невозможность обнаружения постепенных отказов.

Цель статьи – разработка способа обнаружения факта наступления постепенного отказа в двухканальной резервированной системе и определение его вероятностных характеристик.

Способ обнаружения факта наступления постепенного отказа

Рассмотрим двухканальную резервированную систему, в которой сигналы с выходов каналов являются случайными некоррелированными процессами. Будем считать, что случайные величины X и Y , наблюдаемые на выходе каналов в текущий момент времени, характеризуются одинаковыми вероятностными распределениями с параметрами: M [ X ] = M [ у ] = m ; M [ ( X - m ) ² ] = M |^ ( У - m ) ² ] = ст ² . Для сигналов Х и У определим диапазон всех физически возможных значений β и диапазон рабочих (номинальных) значений α. Диапазон α располагается внутри диапазона β (α<β) и разбивает его на три поддиапазона: А 1 – соответствует рабочему диапазону α; А ₂ – расположен ниже диапазона α; А ₃ – расположен выше диапазона α.

Процедура обнаружения факта наступления отказа в двухканальной системе может быть реализована с помощью схемы, представленной на рис. 1.

Обнаружение факта наступления отказа осуществляется в соответствии с критерием

Δ > Δ* – отказ в системе,

Δ ≤ Δ* – система исправна,                                            (1)

где Δ = | X – Y |, Δ^* – пороговый уровень обнаружения отказа, Δ ≤ α^*.

Методика расчета вероятностных характеристик способа обнаружения факта наступления постепенного отказа

Принятие решения об отказе системы в соответствии с критерием (1) носит вероятностный характер. При этом возможны следующие варианты (исходы), составляющие полную группу несовместных событий:

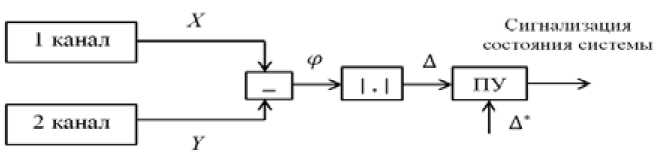
Рис. 1. Схема обнаружения факта наступления отказа в двухканальной резервированной системе

• 1)    выходные сигналы X и Y находятся в диапазоне значений А (отказа нет), а модуль их разности Δ не превысил порог Δ^* (правильное решение об исправности системы);

• 2)    выходные сигналы X и Y находятся в диапазоне значений А ₁ (отказа нет), а модуль их разности Δ превысил порог (ложное решение об отказе системы);

• 3)    один или оба сигнала X, Y находятся в диапазоне значений А 2 или А 3 (отказ одного или обоих каналов), а модуль разности сигналов Δ превысил порог (правильное решение об отказе системы);

• 4)    один или оба сигнала X, Y находятся в диапазоне значений А 2 или А 3 (отказ одного или обоих каналов), а модуль разности сигналов Δ не превысил порог (ложное решение об исправности системы).

Граф состояний системы с возможными исходами процедуры обнаружения отказа представлен на рис. 2, где приняты следующие обозначения: НС – начальное состояние системы; Отк – отказ системы; Исп – исправность системы; ПРО – правильное решение об отказе системы; ЛРИ – ложное решение об исправности системы; ПРИ – правильное решение об исправности системы; ЛРО – ложное решение об отказе системы; P _отк – вероятность отказа системы; Р исп – вероятность исправности системы; Р ппотк – вероятность превышения порога в случае отказа системы; Р _нпотк – вероятность непревышения порога в случае отказа системы; Р _пписп – вероятность превышения порога в случае исправности системы; Р нписп – вероятность непревышения порога в случае исправности системы; Р _прос – вероятность правильного решения об отказе системы; Р лрис – вероятность ложного решения об исправности системы; Р прис – вероятность правильного решения об исправности системы; Р _лрос – вероятность ложного решения об отказе системы.

Введем описание исправного S _исп и неисправных состояний системы S _отк( i , j ):

5 исп = X е А л Y е A ,

S отк ( i,j ) = X _S A Л Y _S A j ,i,J = 1 , 3.

Причем S _отк(1,1) = Ø, так как этот случай соответствует исправному состоянию S _исп. Вероятности введенных состояний равны:

Р исп = J ® X ( X ) - J ® Y ( Y ) dYdX , А ₁ A ₁

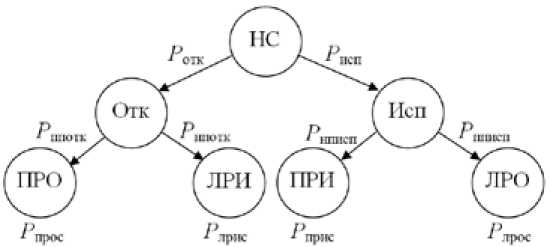
Рис. 2. Граф состояний двухканальной резервированной системы

P OTK ( M ) - J ® X ⁽ X У J ® Y ⁽ Y ) d^YdX , ^{i,j 1} , 3, ^Аi^Aj                                                                                       (3)

где to X ⁽ X ) , to _F ( Y ) ^- плотности вероятности случайных величин X и Y.

В случае исправной системы (состояние S исп ) возможно правильное решение об её исправности или ложное решение об её отказе, вероятности которых Р прис , Р лрос равны:

P = P • P Р = Р • P прис исп нписп , лрос исп пписп , где Рпписп, Рнписп – вероятности превышения и непревышения величиной Δ порога Δ* в случае исправности системы;

Л

^нписп = J ®л(Л / ^1,4) d Л , "    = I ®Л(Л / 4,4) d Л , где од (А/4’4) — условная плотность вероятности величины А при попаданииXи Yв диапазон А1.

В случае неисправной системы (состояния S o_tk ( i,j ) ,i,j = 1 , 3 ) возможны правильные решения об её отказе или ложные решения об её исправности, вероятности которых P ( i,j ) , '.

прос ^{( i,j} )     отк ( ^i,j ) ™ ( ^i,j ) , лрис ^{( i,j} ) ™ ( ^i,j ) нпотк ^{( i,j} ) , i,J ^{, 3                 (6)}

где Р ппотк ( i,j ) , Р нпотк ( i,j ) вероятности превышения и непревышения величиной А порога А * в случае отказа системы;

*

Р ппотк i,jj ) =      ⁾ « л ( А / А . ,А _; ) d А , Р нпотк ( i,j ) = j . _Д ( А / А„А , ) d А, i,j = 1 , 3     (7)

А *                                                                А min ( i,j )

где - /^A i ,A j ) - условная плотность вероятности величины А при попадании X и Y в диапазон A i и A j соответственно, а A m „ ( i,j ) , A max ( i,j ) - минимальные и максимальные значения величины Δ в ситуации S отк . С учетом всех состояний отказа системы получаем вероятности правильного решения об отказе P прос и ложного решения об исправности P лрис :

пр      I"¹ ^ " 1 пр ^ лр

Исходы, соответствующие правильным и ложным решениям о состоянии системы, могут быть объединены в благоприятный и неблагоприятный исходы с соответствующими вероятностями правильного P ПР и ложного P ЛР решений:

р =р +Р р =р +Р

¹ ПР ¹ прис ¹ прос , ¹ ЛР ¹ лрис ^{+ 1} лрос •

Поскольку благоприятные и неблагоприятные исходы являются противоположными событиями, то их вероятности связаны соотношением р +Р =1

1 ПР 1 ЛР 1 •

Выбор порога Δ^* следует осуществлять, исходя из минимизации P_ЛР и максимизации

^A *pt, = ^A rg max Р ПР (^A * ) = ^A rg min Р ЛР (^A * ) .

A * e [ 0 , a ]                           A * e [ 0 , a ]

Пример расчета вероятностных характеристик способа обнаружения факта наступления постепенного отказа

Рассмотрим случай, когда случайные величины X и Y распределены по равномерному закону в диапазоне возможных значений β, причем зона α расположена симметрично относительно математических ожиданий X и Y . При этом значения β выбираем, исходя из заданной веро- ятности безотказной работы каждого из каналов Рк в соответствии с выражением Рк = —, что в обусловлено равномерным законом распределения выходных величин X и Y. Для определения конечных исходов необходимо знать условные плотности вероятностей ®д (д /Ai,Aj) i, j = 1,3, которые могут быть определены по методике, предложенной в [6]. Для расчетов по методике [6] требуются условные плотности вероятностей случайных величин X и Y при условии их нахождения в диапазоне Ai,i = 1,3. Очевидно, что это будут равномерные плотности вероятностей и их определение тривиально.

В силу симметрии рассматриваемого случая справедливы следующие соотношения:

®д(Д / А,А2 ) = од(Д / А1,А3 ) = од(Д / А ,A1 ) = юд(Д / А,A1), д / А2 ,А ) = д / АЛ), . д / АЛ ) = №д(Д / АЛ ).

Кроме того, нет необходимости определять условные плотности вероятностей <у _д ( А /А ^ ,А з ) и Ша ( А /А 3 ,А ) , так как при одновременном попадании случайных величин X и Y в диапазоны A 2 и A 3 ⁽ A 3 и A 2 ) соответственно величина А всегда будет больше порога А * < ^а , т. е. справедливо

Р (2,3) = Р (3,2) = 0,Р (2,3) = Р (3,2) = 1.

нпотк \ ’ 7 нпотк \ *           , ппотк \ * 7 ппотк \ * 7 "

Таким образом, достаточно определить три условные плотности вероятностей ® _д ( А /Ai,A j ) :

_{У д} ( А / A i ,A i ) =<

2- ( a —А ) a ²

А<0

0<^А<^а , ® д ( ^А / ^А 2 ^,A 2 ) =!

А>а

4- ( р^{—а —}2-^А ) ( в — а ) 2

д< 0

о<д< ta ,

^—a

А>--- 2

2-А

® _Д ( А / А 1 ,А 2 ) = <

в- а - а ² l ^ r ^ L в-а - а² в+а -2-А в-а -а^г

Д< 0

0<А< - а ..

—<А<а в+а а<А<---

А> ^а

В результате расчетов с использованием выражений (3)-(8), (12)-(15) определены аналитические выражения для вероятностей конечных исходов:

2 ■ a -A * -

P npuc

= <

a

l в

в

^P P^OC

Л * ²

A

— 0a

a ² -2■ a-A* +A * ²

A * = a

P

, лрос

= <

в

0 < A * <  a

A = a

Р ² - а ² - 2 - Р-А* + 2 - а -А * в ² 0 <А <а

P

, лрис

2 - Р -А * - 2 - а -А * Р

0 <А * ■

.

С использованием выражений (16), (17) получены графические зависимости вероятностей

• ложных и правильных решений, от отношения порога к рабочему диапазону А / и фиксиро- а ванного значения Рк = —, представленные на рис. 3, 4. Р

Проведя вычисления благоприятных и неблагоприятных решений с использованием выражения (9), получим графические зависимости, представленные на рис. 5.

Из приведенных на рис. 5 зависимостей видно, что существует оптимальное значение порога А = А , которому соответствует максимальное значение вероятности правильных ре- opt                                                                                                          _*

шений и минимальное значение ложных решений. Причем значения А opt, РПР (A opt), РПР (A opt) а зависят от соотношения :

в

I . • а I                      I Л - а

.

= Arg тахР ПР \ А , — 1 = АrgminP _ЛР\ А ,— k Р'               к Р.

А * е [ 0 , а ]                                 А * е [ 0 , а ]

Заключение

В классических резервированных системах выбор оптимального значения порога Δ* осуществляется из условия равенства вероятности ложного решения об отказе системы нулю

а                                    б

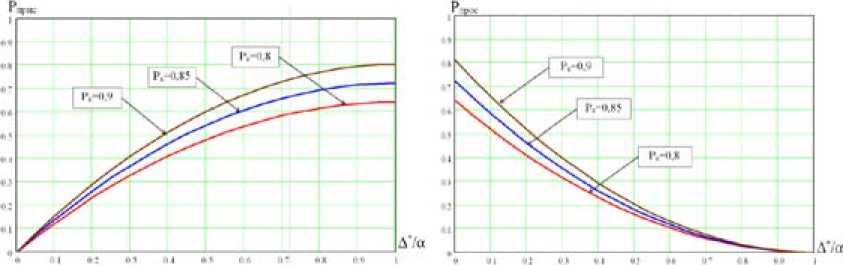
Рис. 3. Зависимости вероятности правильного решения об исправности системы (а) и вероятности ложного решения об отказе системы (б) от отношения ^/ при фиксированных Р_р а

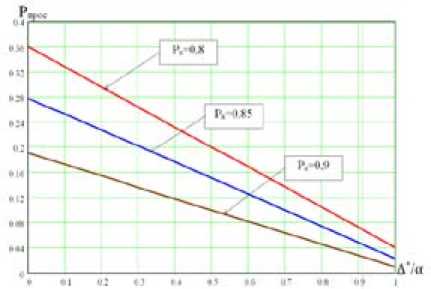
Рис. 4. Зависимости вероятности правильного решения об отказе системы (а) и вероятности ложного

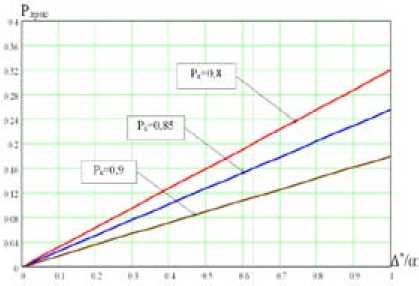
б

решения об исправности системы (б) от отношения

*

^А а при фиксированных Р _к

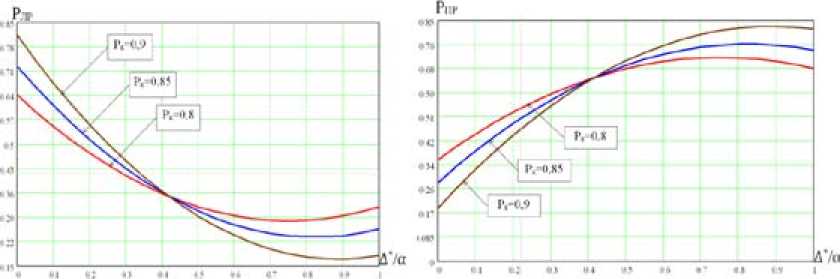
а                                               б

Рис. 5. Зависимости вероятностей ложных решений (а) и правильных решений (б) от отношения А * / при фиксированных Р к

(Δ* = α), так как в многоканальных резервированных системах (число каналов 3 и более) ложное решение об отказе системы приводит к исключению из дальнейшей работы исправного канала. В двухканальных резервированных системах, где факт обнаружения отказа является сигналом для подключения других устройств проверки, необходимо оптимизировать порог Δ* таким образом, чтобы минимизировать вероятность принятия ложного решения об исправности системы при фиксированном максимально допустимом значении вероятности принятия ложного решения об отказе системы.

Выбор значения порога Δ* в двухканальных резервированных системах следует с учетом

а

отношения в, что обеспечит максимум вероятности правильных решений и минимум вероят- ности ложных решений о состоянии резервированной системы.