Способ обработки результатов кавитационных испытаний насосов турбонасосных агрегатов с целью получения аппроксимирующей функции

Одним из наиболее ответственных и энергонапряженных узлов жидкостного ракетного двигателя является турбонасосный агрегат (ТНА), необходимый для обеспечения непрерывной подачи компонентов топлива в камеру двигателя с заданным расходом и давлением. К ТНА, как к агрегату жидкостного ракетного двигателя (ЖРД), предъявляются следующие требования:

• –    обеспечение работоспособности и основных параметров при заданном ресурсе с необходимыми возможными паузами установленной продолжительности;

• –    обеспечение на всех режимах работы двигателя подачи компонентов топлива требуемого расхода и давления при высокой степени надежности с приемлемым КПД всего агрегата и минимальной стоимости изготовления;

• –    обеспечение минимальных размеров и массы всей двигательной установки (ДУ) за счет наименьших габаритных размеров и массы самого ТНА.

При работе ТНА, в насосе может возникнуть явление кавитации, отрицательно влияющее на выполнение указанных выше требований. Кавитацией называют процесс роста пузырька в жидкости вследствие динамического понижения давления до давления насыщенного пара, происходящий при постоянной температуре [1]. Данный процесс схож с кипением (рост пузырька, вызванный повышением температуры жидкости). При кавитации сам пузырек в жидкости динамически меняется: сначала происходит рост, затем, если на него не будет действовать возрастающее давление, рост сначала прекратится и начнется сжатие пузырька. Затем пузырек схлопнется и, вероятно, исчезнет вследствие растворения газов и конденсации пара. Схлопывание происходит «скачком», если паровые пузырьки, или каверны, содержат малое количество газа, и менее резко, если содержание в них значительно. Таким образом, кавитация включает целый ряд явлений от зарождения пузырька до его схлопывания [2]. Само же явление ведет к понижению рабочих параметров насоса, что может отразиться на работе жидкостного ракетного двигателя в целом. При более длительном воздействии, вследствие местных повышений давления из-за схлопывания пузырьков, кавитация вызывает деформацию крыльчатки насоса – так называемую кавитационную эрозию.

Вследствие воздействия кавитации возникает вопрос об учете данного явления при проектировании ТНА и разработке методики, позволяющей смоделировать кавитационное течение при работе насоса. Такие методики существуют, например они описаны в работах [3; 4]. Также существуют методы вычислительной гидродинамики CFD, позволяющие численно смоделировать кавитационное течение в различных агрегатах (крыльчатка насосов, винт турбины, гидрокрыло, различные объекты в жидкости) и с применением сред с различной вязкостью и поверхностным натяжением, в том числе и криогенных. Данные методики представлены в работах [5–7].

С технической точки зрения, насосы окислителя и горючего предназначены для подачи компонентов топлива в газогенераторы и коллектор подвода камеры двигателя. Основным рабочим элементом насоса является крыльчатка закрытого типа с односторонним входом, реже двусторонним [8]. Для улучшения антикавитационных качеств насоса на входе перед крыльчаткой устанавливается шнек. Обычно крыльчатки отливают из высокопрочного алюминиевого сплава, шнек изготавливают из нержавеющей стали.

При изготовлении ТНА насосы подвергаются целому ряду испытаний на экспериментальное определение количественных и качественных характеристик объекта как результата воздействия на него сил при его функционировании, среди которых и испытание на определение кавитационного срыва. Как и в общем машиностроении, для испытаний насосов ТНА можно выделить виды испытаний, которые можно классифицировать по организационно-юридическому признаку, их содержанию, составу, месту проведения и объектам испытаний [9]. Согласно данной классификации, испытания насосов на определение кавитационного срыва можно определить к приемо-сдаточным по организационно-юридическому виду, параметрическим – по содержанию, кавитационным – по составу и стендовым – по месту проведения.

Вследствие ряда допущений в различных моделях кавитации, теоретические и практические данные имеют определённое расхождение. Данное расхождение должно быть учтено с учетом специфики работы насоса ТНА, а именно высокого перепада давлений при малых габаритах рабочего колеса. Целью работы является разработка методики аппроксимации данных гидравлического пролива насосов ТНА для дальнейшей верификации полученной модели с данными испытаний насоса с другой геометрией. Разработка и совершенствование новых методов численного моделирования гидродинамических процессов ведет к повышению энергоэффективности и КПД ТНА и ЖРД в целом.

Описание средств измерений

Средства измерений (СИ) для данных испытаний выбиралась так, чтобы погрешность измерения отдельных параметров на режиме испытаний, определяемая классом точности СИ, не превышала заданных значений:

• –    для расходов ±1,5 %;

• –    давлений ±1,0 %;

• –    перепада давлений ±1,5 %;

• –    температуры воды ±1 %.

Для измерения давления используются образцовые манометры класса 0,4 по ГОСТ 65217–72. Также, при проведении натурных испытаний на определение кавитационного срыва, разрешается применять манометры точных измерений класса 0,6 по ГОСТ 2405–88. Манометры выби- раются с таким диапазоном шкалы, чтобы измеряемые значения параметра находились во второй трети шкалы прибора. Подготовка манометров и эксплуатация при стендовых испытаниях осуществляется в соответствии с ОСТ 92-1608–80.

Все приборы должны располагаться в правильном положении с обеспечением их устойчивости. Положение самого наблюдателя при всех его действиях не должно вызывать препятствий при записи показаний [10].

Определение и исключение промахов

Обычно данные испытаний записываются в виде зависимости напора по оси Y, выраженного в метрах или в Дж/кг, к давлению на входе по оси X, выраженному в Па или кгс/см ² . Для возможности сравнения показаний кавитационных испытаний с аналогичными показаниями других насосов, а также определения функции приведем значения к безразмерным коэффициентам. Для оси Х будем использовать число кавитации σ [2] записанное в следующем виде:

σ=

2( P вх - P v )

ρ*v2    , вх ср

где Р вх – давление на входе в МПа; Р v – давление насыщенного пара в МПа; ρ – плотность жидкости в кг/м ³ . Для оси Y будем использовать коэффициент напора Ψ (англ. head coefficient). Данный коэффициент применяется в достаточном большом числе работ, например в статьях [11–13]:

Ψ= 2* g * H ₂ , (2) v 2²

где H – полный напор насоса в м; v 2 – скорость на выходе из насоса в м/с ² .

Результаты гидравлических испытаний со снятием кавитационной характеристики модельного (подобного натурному) насоса с полученными значениями давления входа, давления выхода, расхода, числа оборотов крыльчатки заносятся в таблицу. Для каждого испытания снимаются показания параметров давления на входе и выходе из насоса, а также расхода в 12–13 точках. В данной статье рассматриваются результаты 78 виртуальных испытаний с суммарным числом в 944 точках, представленных на рис. 1. Для определения точек промахов воспользуемся критерием Шовене, основанном на распределении Гаусса. Для этого определяется число стандартных отклонений с учетом всех результатов, в том числе и потенциальных промахов, а затем сравнивается с вероятностью повторения данного события. Значение вероятности определяется с помощью распределения Гаусса. Для точного определения промахов, разобьём все точки, представленные на рис. 1 на группы справа налево по интервалам значений σ: 1-я группа σ = [0,26–0,25], 2-я [0,24–0,23], 3-я [0,22–0,21], 4-я [0,17–0,18], 5-я [0,15–0,16], 6-я [0,13–0,14], 7-я [0,125–0,13], 8-я [0,12–0,125], 9-я [0,115–0,12], 10-я [0,11–0,115], 11-я [0,104–0,11], 12-я [0,095–0,104], 13-я [0,09–0,095]. В каждой группе 78 точек данных, за исключением 13-й, в которой 8 точек. Для работы с критерием Шовене подсчитано для каждой группы значения среднего числа и среднеквадратического отклонения. Рассмотрим выполнения критерия Шовене для всех 13-ти групп.

В первом приближении не подошли под критерий Шовене (значение числа точек значений испытаний, умноженное на вероятность повторения должно быть не ниже 0,5) нижние точки в группах с 12 по 5. Уберем из рассмотрения данные точки. Следовательно, число точек уменьшится для этих групп с 78 до 77, соответственно. Повторно рассчитываем критерий Шовене для данных групп.

По результатам второго приближения все точки 1–6 группы подошли под критерий Шовене, когда нижние точки групп 7–12 нет. Повторно убираем из рассмотрения точки испытания. В группах 7–12 число точек уменьшится с 77 до 76 соответственно.

По результатам третьего приближения не подошли под критерий Шовене нижние точки 9-й, 11-й и 12-й групп. Аналогично убираем из рассмотрения данные точки. После данного приближения можно утверждать, что грубых промахов во всех группах нет, так как критерий Шовене выполняется для всех 12-ти групп.

Отдельно рассмотрим точки 13-й группы. В данной группе грубых промахов нет, для учета испытаний подходят все 8 точек. По результатам отбрасывания промахов, общее число точек для рассмотрения уменьшилось с 944 до 927.

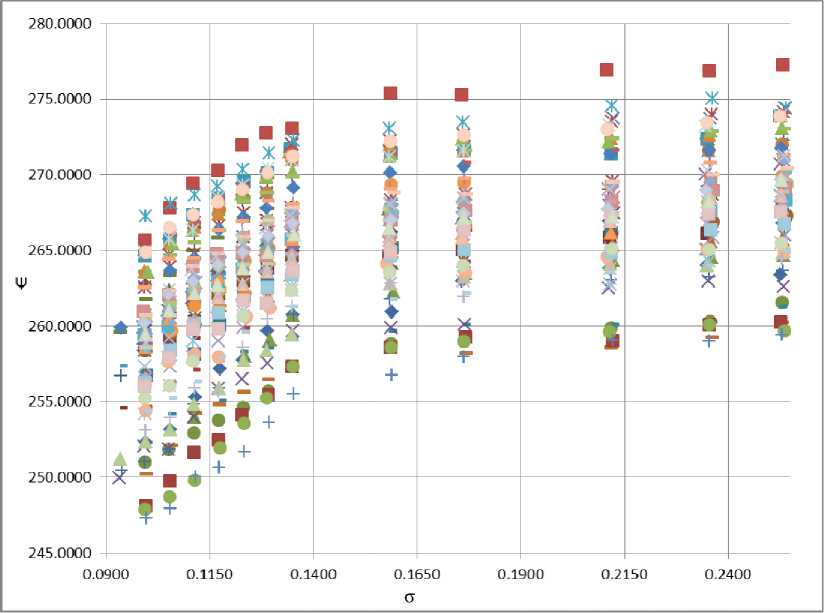
Рис. 1. График данных испытаний

Fig. 1. Plot of test data

Аппроксимация результатов испытаний

Для определения функции, ее характера (линейная, степенная, логарифмическая и т. д.), необходимо воспользоваться одним из методов математического анализа – аппроксимацией. Для аппроксимации полученных результатов с целью получения зависимости воспользуемся методом наименьших квадратов [14]. Метод заключается в рассмотрении суммы квадратов разностей y_i , полученных при кавитационном испытании и аппроксимирующей функции φ( x ) в соответствующих точках. Параметры функции a , b , c … n φ( x ) подбираются так, чтобы разность в квадрате была наименьшей. В зависимости от вида функции: линейная вида y = ax + b , трехчлена второй степени y = ax ² + bx + c и т. д. – различаются системы линейных уравнений, необходимых для получения неизвестных a , b , c .

При рассмотрении общего для всех 78 испытаний поведения значений коэффициента напора Ѱ от числа кавитации σ, можно сделать вывод о невозможности аппроксимации значений линейной зависимостью. В качестве аппроксимирующей функции необходимо рассмотреть логарифмическую, экспоненциальную и степенную функции.

В случае аппроксимации логарифмической функцией, зависимость задается в виде F ( x ) = a + b * ln( x ). В случае аппроксимации экспоненциальной функцией, зависимость задается в виде F ( x ) = a * e^{b * x} . В случае аппроксимации степенной функцией, зависимость задается в виде F ( x ) = a * x^b . Используя метод наименьших квадратов, получим следующие уравнения аппроксимации, описывающие все 927 точек значений испытаний:

F ( x ) = 283.106 + 9.742*ln ( x ) ;

F ( x ) = 255.799* e ⁽⁰ .2 ¹³ * x ) ;

F ( x ) = 283.78* x ^0.0369

По полученным уравнениям построим график для каждого уравнения и сравним их со средними значениями групп 1–13 испытаний. График представлен на рис. 2.

Наиболее близкие показания аппроксимации и значений испытаний насоса в режиме кавитации (крайние левые значения точек на графиках) показывает степенная функция (5). Для дальнейшей работы по приближению аппроксимирующей функции к показаниям испытаний будет взята за основу степенная функция.

Чтобы приблизить значения аппроксимирующей функции (5) к графику средних значений испытаний, зададимся коэффициентами для функции Ѱ: a = 0,35, b = –0,092456 и c = 1,0239. Запишем, полученное аппроксимирующее уравнение и сравним его с данными средних значений испытаний (рис. 3):

a *0, 0369                                     0,35*0,0369

с + b ) ^, C - 0,092456) , ^, T = 283,78 ⁽ )----- = 283,78 ⁽     ,        )------- .

c                       1,0239

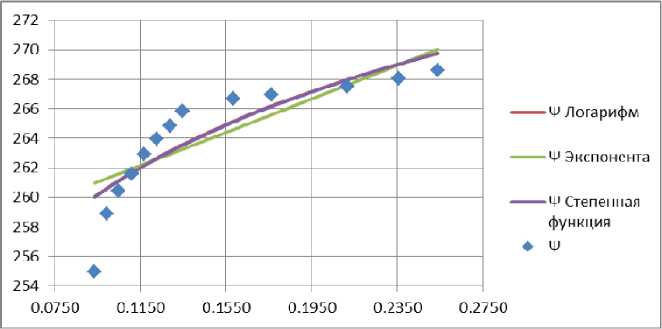
Рис. 2. График средних значений групп испытаний и их аппроксимации

Fig.2. Plot of means of test groups and their approximations

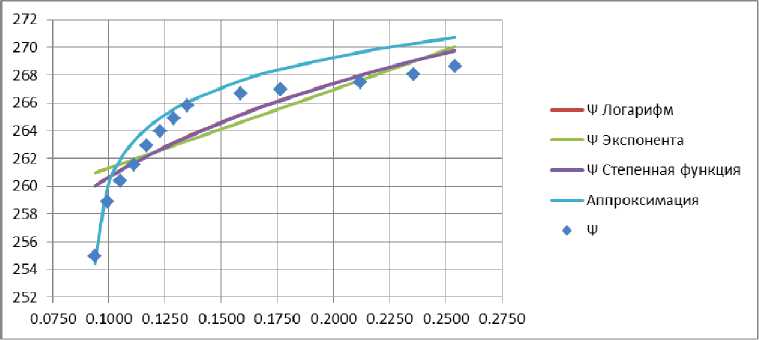
Рис. 3. График средних значений групп испытаний и сравнение с аппроксимирующем уравнением, логарифмической, экспоненциальной и степенной аппроксимацией

Fig. 3. Plot of test group means and comparison with fitted equation, logarithmic, exponential, and power approximation

Максимальная относительная погрешность уравнения (6) и средних значений испытаний групп 1–13 (рис. 1) равна 0,97 %. Однако, если сравнивать уравнение (6) со значениями каждого испытания из групп точек на рис. 1 по отдельности, то максимальная относительная погрешность будет равняться 4,59 %. Для более точного приближения уравнения к данным испытаний, рассмотрим отдельные испытания с минимальными и максимальными значениями Ψ. Введем новые коэффициенты для уравнения (6), чтобы понять характер смещения аппроксимирующего графика относительно значений Ψ. Коэффициент степени a оставим равным 0,35, а коэффициенты для значений b примем –0,094 и –0,0957, для значений c примем 0,998 и 1,07 для минимального и максимального испытания соответственно. Запишем полученные аппроксимирующие функции:

(ст - 0.094)^{0, 0,0369}

V = 283,78 (--------)------

0.998

(ст - 0.0957)^{0, 0,0369}

V = 283,78 (----------)-------.                          (8)

1.07

Для определения общей для всех испытаний аппроксимирующей функции, зависимой от номинального значения Ψ, представим зависимость Ψ от коэффициента в линейном виде y = a * x + c , получим систему уравнений для коэффициента b и c функций (6), (7) и (8):

( - 0,094 = a *277.2724 + c

,                                  ;                                              (9)

- 0.0957 = a *259.4448 + c

Г0.998 = a *277.2724 + c

• 1 .07 = a *259.4448 + c

Запишем полученное аппроксимирующее уравнение для всей группы испытаний

V = 283,78

( ст + ( T*0,000093577 - 0,12044 ) ) ^0,3 5* ^0,03 6 ⁹ ( - T*0,00403 8 + 2,11762 )

Формула (11) приближает значения функции к данным испытаний, за исключением данных, находящихся в значениях испытаний близких к средним. Данное отличие становится очевидным, если рассмотреть зависимость коэффициентов b и c от Ψ. Для еще более точного приближения функции (11) к данным испытаний обратимся к методу интерполяции функций при помощи алгебраических многочленов (полиноминальная интерполяция). Воспользуемся интерполяционной формулой Ньютона для неравных промежутков [15]. Данная формула является видоизменённой формулой Лагранжа и в общем виде ее можно записать f (x) = B1 +(x - x1) B2 +(x - x1)(x - x2) B3 + ... + ( x - x1) *•••* (x - xn-1) Bn. (12)

С помощью разделенных разностей, составляя интерполяционную таблицу, находим коэффициенты B1, B2, B3…Bn. Для коэффициентов разности b и деления c получим уравнения aразн = -0.094 + (6.27205*10-5) * (Tн - 277.2724) -

- ( 3.66748*10 - 6 ) * ( T н - 277.2724 ) * ( T н - 268.3439 ) ;                (13)

a дел = 0.998 - 0.00290082 * ( T н - 277.2724 ) +

+ 0.000127862* ( T н - 277.2724 ) * ( T н - 268.3439 ) .                 (14)

Учитывая, что в данных восьми испытаний присутствуют 13 точек замеров вместо 12, изменим коэффициент –0,094 в формуле (13) на коэффициент –0,092, окончательно формула коэффициента разности b будет выглядеть:

а разн = - 0.092 + ( 6.27205*10- 5 ) * ( T н - 277.2724 ) - ( 3.66748*10 - 6 ) * ( Т н - 277.2724 ) * ( Т н - 268.3439 )

Запишем окончательную функцию аппроксимации испытаний

Т = 283,78

(ст + а разн

) 0,35*0,0369

дел

Максимальная относительная погрешность, при сравнении функции (16) с каждым графиком испытаний по отдельности, не превышает значений 1,9 %. Преимущественно, погрешность находится в пределах 1 % для большинства точек. Данные значения можно считать удовлетворительными.

Заключение

В ходе анализа результатов, выявлена общая хорошая сходимость данных испытания и функции (16). Аппроксимирующая функция может иметь расхождения в начале кавитационных испытаний, однако в области кавитационного срыва приближается к значениям испытаний. При рассмотрении относительной погрешности для всех испытаний (исключая грубые промахи) функция показывает применяемость к данным испытаний. Дополнительный охват минимальных и максимальных значений испытаний дал более точные приближения к данным испытаний. В некоторых сравнениях данные функции и испытаний могут отличаться сильнее, что объясняется учетом всех данных испытаний, в том числе вышедших за заданные конструкторской документацией пределы.

Для дальнейшей работы необходимо уточнить коэффициент b и c с целью увеличения диапазона охвата значений σ и Ψ, а также увеличения точности приближения. При рассмотрении результатов аппроксимации в части возможности применения функции (16) к аналогичной аппроксимации значений испытаний других высоконапорных насосов, необходимо уточнить коэффициенты a , b и c . Коэффициенты можно уточнить, применяя для функции (16) как данные кавитационных испытаний других насосов (особенно в данной части интересно приближение функции к результатам испытаний других высоконапорных насосов, характерных для ТНА), так и другие методы интерполяции и аппроксимации коэффициентов и функции. Таким образом, полученный способ позволит проводить анализ кавитационных свойств центробежного насоса с целью улучшения антикавитационых качеств ТНА, тем самым позволяя выполнить современные требования по энергоэффективности, предъявляемые к новым разрабатываемым ТНА ЖРД.