Способ оценки дальности до подводного объекта по кривизне волнового фронта в условиях воздействия коррелированного шума

Вместе с тем стремление разработчиков ИГС к увеличению дальности их действия и повышению разрешающей способности по угловым координатам при наблюдении за ПО и связанная с ними тенденция к увеличению размеров антенн приводят к тому, что в ряде случаев пренебрегать кривизной волнового фронта в пределах раскрыва приемной антенны практически невозможно.

Основная часть

С точки зрения кривизны волнового фронта, обрабатываемого ПВС, всю область пространства, где могут находиться источники сигналов, можно разделить на три зоны, отсчитываемые относительно приемной антенны [2]:

• 1)    ближнюю, когда r _б ² _з ≤ 0,38 L ³ λ ,

где r – дальность объекта; L – габаритный размер антенны; λ – длина волны;

2L2

• 2)    зону Френеля, когда r _бз < r _зф < _λ ^L ;

2L2

• 3)    дальнюю зону, когда r д_з ≥     .

В зависимости от нахождени ^λ я ПО в одной из указанных зон в ИГС применяется соответствующая модель формирования ПВС.

Рассмотрим новое математическое решение для оценки дальности до ПО по кривизне волнового фронта (ВФ), находящегося в зоне Френеля, на основе анализа пространственной частоты.

Примем в качестве модели ПО точечную модель отражающего (излучающего) объекта, который создает в однородной безграничной среде сферическую волну. Такая модель является основной для анализа ПВО сигналов реальных морских объектов, так как эти объекты во многих случаях хорошо описываются моделью в виде некоторого набора «блестящих» точек [3].

Соотношения, справедливые для точечного объекта, применимы также и для малоразмерных объектов при условии, что их величины много меньше элемента разрешения системы ПВО сигналов [1–3].

Для теоретического описания процесса формирования ПВС в зоне Френеля антенной решетки построим графическую модель (рис. 1).

На рис. 1 r - дальность, r o - дальность объекта, m - номер элемента АР, - 0,5 ( M - 1 ) <  m <  0,5 ( M - 1 ) ; M – число элементов, d – расстояние между элементами АР, n – номер отсчета во временной области, n = 0... N - 1, N - число отсчетов.

Так как зондирующий сигнал предполагается гармоническим, то ПВС в m-м элементе АР определяется выражением s (m, n ) = a • exp j 2nfо I n

c

r 2 + ( md ) 2

f

a • exp

j^{2 n} f 0 n

V

г f d m ro 1 + u m c У V ro

f‘ где a - амплитуда сигнал; f0 = — fд

- нормированная частота; f‘ - частота сигнала; fg - частота дискретизации; m – номер элемента в антенной решетке (АР).

Для дальнейших рассуждений значение амплитуды не играет существенной роли, поэтому будем рассматривать ПВС вида

5 ( m , n ) = exp

j2nf0 n - r0 c

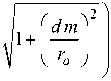
Модель ПВС в зоне Френеля может быть представлена следующим образом [2]:

■

(

1 | dm |

I ^{1 +} 2 V ^

V              //

r

5 (m, n ) = exp j2nf0 n - o-_ V

= exp ( j2.Л f • n ) • exp - j 2 nu • m ² + j^, 00

fo • d2         f Г                                   2n где uо = -0---; ф = 2nf о • -° = kо • ro - начальная фаза; kо = — - волновое число; Xo - длина вол-

² r o ^c                c                                     A)

ны.

Как видим из выражения (3), ПВС факторизуется в виде произведения временной и пространственной составляющей и имеет вид [4]

s ( m , n ) = s 1 ( n ) • s 2 ( m ) ,

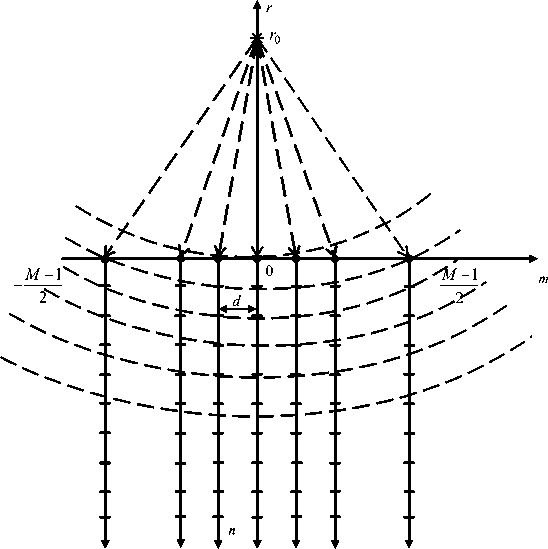
Рис. 1. Модель формирования ПВС в зоне Френеля антенной решетки

Fig. 1. Model of the formation of space-time signal in the Fresnel zone of the antenna array

где 5 1 ⁽ n ) = exp ⁽ j 2 ⁿ f о • n ) ^{; 5} 2 ⁽ m ) = exp ⁽- ju о • m 2 ₊ j _V ) .

Причем, как видим из (3) и (4), информацию о дальности несет пространственная составляющая s ₂ ( m ).

Полагая, что ПО малоподвижен, и учитывая, что 5 1 ( n ) = exp ( j 2 пf 0 • n ) , для выделения составляющей 5 2 ⁽ m ) умножим ^{5 (} m, n ) на ⁵ * ⁽ n ) , где «*» ^- знак комплексного сопряжения;

5 1 ⁽ m ) = 5 1 * ⁽ n ) • ^{5 (} m , n ) = exp ( ^- j 2 ^И о • m 2 + ]ф ) .

Выражение для s (m) включает квадратичную пространственную переменную m2, что 2, существенно усложняет обработку такого сигнала для выделения из него величины r0. Для упрощения обработки воспользуемся следующим приемом: сдвинем s2 (m) на p отсчетов и перемножим с исходным комплексно сопряженным

*(                                                   2\

Z ⁽ m ) = ⁵ 2 ⁽ m ^- p \ ⁵ 2 ⁽ m ) = ^{exp (} j ^{2 n} ^ ^{2 u} о p • m ^- j ^{2 n u} о • p ) =

= exp ( j 2 nv 0 • m + jY ) , pd ²

где v 0 = 2 p • u 0 = ——; Y = - 2 n u ₀ • p - начальная фаза. Л) ^г о

В результате проделанных преобразований получим гармонический сигнал частоты v0 и задача определения дальности до ПО свелась к определению пространственной частоты v , 0, откуда [5]

pd ²

/Q =         .

^^v 0

В настоящее время известно большое количество методов оценки частоты гармонического сигнала [6]. Для примера рассмотрим метод дискретного преобразования Фурье (ДПФ) для оценки v 0

0 5(M 1)

Z ⁽ v ) = S 2 ⁽ m ) . exp I^- j ^v • m

-0,5( M-1)+ p

0,5( M-1)                                    (2

S     exp ( j 2 n v 0 • m + j V ) ■ exp I - j-v - m

• -0,5( M-1)+pV

  0 5 ( M - 1 )

  = exp ( j v ) •     S

  ^- 0,5 ⁽ M ^{- 1 )+} p

  
  

  2 n

  exp    M ⁽"- M ' v ^{0 )}' m

  
  

  .

  
  

Модуль выражения (8) имеет максимальное значение, когда v = M ∙ v ₀. И тогда согласно выражению (7) [7]

pd ² pd ² • M ---=------

• A) v 0      A) v

Приведенные выше рассуждения не учитывают влияние окружающей среды на формирование ПВС.

Однако в реальной обстановке ПВС s (m, n) испытывает искажающее воздействие окружающей среды в виде аддитивной составляющей ω (m, n), куда отнесем шум элементов АР и помехи гидроакустического канала x (m, n ) = s (m, n) + ®(m, n), (10) где ω (m, n) – стационарный гауссовский шум с нулевым средним и корреляционной матрицей Cww = E[W(m,n)• WH (m,n)];«н»- гильбертово сопряжение, W(m, n)- вектор шума.

Представим сформированный ПВС АР в векторно-матричном виде [8]

"   x ( - 0,5 ( M - 1 ) ,0 ) M x ( - 0,5 ( M - 1 ) , ( N - 1 )) ■L x ( 0,0 ) M x ( 0, N - 1 ) ■L x ( 0,5 ( M - 1 ) ,0 ) M x ( 0,5 ( M - 1 ) , N - 1 ) 144442X 44443

I S 1 ( 0 )         0       L       0 । M                                               M                                                                 M S 1 ( N - 1 )      0      ^      0 0         S 1 ( 0 )     L       0 M                                               M                                                                 M 0      s , ( N - 1 ) L      0 0         0       ^ s 1 ( 0 ) M                                               M                                                                 M _     0          0       L s j ( N - 1 )_ 14444444244444443 H

~S 2 ( - 0,5 ( M - 1 ))1 M S 2 ( 0 ) M [ S 2 ( 0,5 ( M - 1 ) 4 ] θ

® ( - 0,5 ( M - 1 ) ,0 ) M ® ( - 0,5 ( M - 1 ) , N - 1 ) ■L * M " ) „ ( « . N - 1 ) ® ( 0,5 ( M - 1 ) ,0 ) M 1 ( 0,5 ( M - 1 ) , N - 1 3 W

( )

Перепишем выражение (11) в более компактном виде

X = H • 0 + W ,

где X – ( MN × 1) вектор ПВС; H – ( MN × M ) известная матрица, формируется в приемнике; θ – ( M × 1) вектор оцениваемых параметров; W – ( MN × 1) вектор шума.

Требуется получить несмещенную оценку вектора θ ^ˆ с минимальной дисперсией. Для получения такой оценки воспользуемся теоремой Гаусса-Маркова [9, 10], которая утверждает, что если данные представляются линейной моделью вида (11), в которой шумовой вектор W с произвольной плотностью функции распределения, нулевым средним и известной ковариационной матрицей C _ww =E I W • W I , «н» - операция гильбертово сопряжение, то лучшая несмещен- ^{[         ]}

ная оценка в классе линейных оценок имеет вид

-1

⁹ ■ ^HH^С” ' ^н ) ■ " ^С™ X .                                            ⁽¹³⁾

При этом минимальная дисперсия оценок дается выражением var(’m )= (HH CW.-H)

- 1

mm

Выражение [A] mm означает выделение диагональных элементов квадратной матрицы A .

Если шумовая составляющая W представляется белым гауссовским шумом с ковариационной матрицей σ² ∙ I , где I – единичная матрица, σ² – дисперсия, то выражение (13) и (14) преобразуется соответственно [5, 6] в

0 = ( H H xH ) . H H . X                                                        (15)

и var(<>m )" »2

( H « . H ) —1

mm

Выполняя вычисления в соответствии (13) или (15), фактически мы получим оценки s2 (m) с минимальной дисперсией. Дальнейшие расчеты для получения окончательного результата, т.е. определения дальности до объекта, необходимо проводить в соответствии с выражением (6), (8), (9).

Заключение

Как показано в изложенных материалах, кривизну волнового фронта ПВС можно использовать для определения дальности до ПО, когда он находится в зоне Френеля относительно приемной АР. Модель образования ПВС (3) позволяет факторизовать его на временную и пространственную составляющие (4), что позволяет проводить независимую обработку по временной и пространственной координате. Кроме того, это дает возможность представить сформированный на АР ПВС реальный сигнал в виде линейной векторно-матричной модели (11) и применить хорошо известные теоремы минимизации дисперсии оценок (13), (15). Однако обработка по пространственной координате серьезно осложняется наличием квадратичной переменной (5). Введенный прием сдвига и перемножения позволяет представить сигнал по пространственной координате в виде гармонического, пространственная частота которого зависит от дальности до ПО (6). В результате проделанных операций задача определения дальности ПО в зоне Френеля свелась к оценке пространственной частоты (8).