Способ определения объектов с нерациональным электропотреблением в инфраструктуре бюджетных организаций и учреждений муниципального уровня

Отправной точкой развития программы повышения энергетической эффективности любой организации в свете Федерального закона Российской Федерации № 261-ФЗ является энергоаудит, который дает фиксируемую картину текущего состояния энергоэффективности, позволяет проанализировать использование энергетических ресурсов, затраты на них, выявить места нерационального использования ресурсов, разработать программу энергосберегающих мероприятий и проектов.

Способом определения в составе инфраструктуры бюджетных организаций и учреждений муниципального уровня объектов, в течение длительного времени аномально потребляющих электроэнергию и поэтому требующих первоочередного энергетического обследования, может

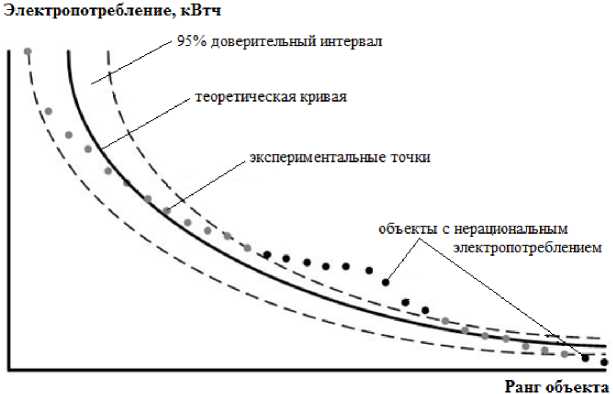
Рис. 1. Определение объектов с нерациональным электропотреблением

служить одна из важнейших аналитических процедур рангового анализа [1, 3] – интервальное оценивание параметрического рангового распределения [2] (рис. 1).

Ранговый анализ начинается с построения ряда табулированных ранговых распределений по величине электропотребления, учреждению с максимальной величиной электропотребления W max = W i присваивается ранг r 1 , следующий объект с W ₂ = W 1 имеет ранг r 2 и т. д. для всей выборки. Учреждение, имеющее минимальное электропотребление W_mi „ = Wn , будет иметь ранг r N , равный общему числу организаций N .

Ранговое распределение бюджетных организаций и учреждений муниципального уровня по электропотреблению разбивается на несколько интервалов с учетом следующих допущений:

• -    в каждом интервале должно быть не менее 10–12 точек,

• -    отклонения действительных значений электропотребления от соответствующих значений, полученных в результате аппроксимации, должны быть распределены внутри интервала по нормальному закону.

При этом для каждого интервала можно записать уравнение вида [2, 3]:

t^(Z5>i = Ф ' ЙО-

где Δ – ширина доверительного интервала в одну сторону от теоретической кривой; σ(ΔΘ) – среднеквадратичное отклонение экспериментальных точек от теоретической кривой (в расчетах

-с ²

принимается эмпирический стандарт); Ф^-1 (—) - обратная функция Лапласа Ф(t) = — Г е” dt 2                                              2^ О

; p d – доверительная вероятность (принимается априорно).

Решение уравнения (1) позволяет определить ширину доверительного интервала на каждом из участков разбиения.

Современное компьютерное прикладное программное обеспечение позволяет осуществлять быструю, эффективную и корректную обработку данных любых объемов и сложности. Способ определения объектов с нерациональным электропотреблением реализован в пакете MathCAD на примере инфраструктуры образовательных учреждений Нерюнгрин-ского района.

Подготовка данных

После сбора информации об электропотреблении инфраструктуры образовательных учреждений создается электронная база данных, которая представляет собой неупорядоченную совокупность значений электропотребления объектов инфраструктуры, сформированная в виде двумерной таблицы. Строки таблицы соответствуют временным интервалам, в течение которых исследовалась инфраструктура, а столбцы – объектам инфраструктуры. В каждой ячейке таблицы содержится одно число, соответствующее электропотреблению (в кВтч) одного объекта на одном временном интервале. Данные должны быть сохранены в файле Microsoft Excel «data.xls», который помещается в директорию «c:\mathcad_dat», заблаговременно созданную в корневом каталоге диска «c:\». Далее уже программными средствами осуществляется импорт данных из файла «data.xls» в тело программы MathCAD

V :=         В

Сформированная двумерная матрица V содержит информацию об исследуемой инфраструктуре, причем каждая строка соответствует определенному временному интервалу (году), а каждый столбец - объекту. Для исследования использовались собранные за восемь лет данные по электропотреблению инфраструктуры образовательных учреждений (49 объектов), расположенных на территории Нерюнгринского района.

Для упрощения дальнейшей работы в MathCAD матрицу необходимо транспонировать, чтобы ее колонки являлись векторами параметров: W := V T .

В дальнейшем имеющиеся неупорядоченные фактические данные по электропотреблению нужно проранжировать, т.е. расположить данные в порядке уменьшения значений электропотребления.

Листинг 1. Получение табулированного рангового распределения

^Р/(Г) -

for i ∈ 1 .. cols(Y) c←sort(Y〈i〉) 〈i〉 b ← reverse(c) b

С целью подготовки данных для дальнейшей работы программы определяется количество исследуемых объектов п ^ length(Zip/(^)<1>) = 49

и формируется вектор рангов: r := 1.. n , R _r := r.

Для оценки динамики движения объектов инфраструктуры образовательных учреждений по ранговой поверхности параметрического распределения необходима матрица рангов.

Листинг 2. Определение рангов для каждого объекта

Rang(^) —

for j e 1.. cols(W)          Rang(W) — Rang(VT)T i←1

a←W〈j〉 c ← sort(a)

b ← reverse(c)

for m ∈ 1 .. rows(a)

for n ∈ 1 .. rows(b)

Li, j← n if am bn i←i+1

L

Для последующей статистической обработки данных большое значение имеет подбор аналитической зависимости, наилучшим образом описывающей совокупность эмпирических точек. В качестве стандартной задается двухпараметрическая гиперболическая форма [1,2]

^(У) — 2К выбор которой объясняется традиционно сложившимся подходом среди исследователей, занимающихся ранговым анализом. Достоинство данной формы состоит в том, что она сводит задачу аппроксимации к определению всего двух параметров.

Аппроксимация может осуществляться различными методами, каждый из которых обладает как достоинствами, так и недостатками. Например, метод наименьших квадратов. Суть метода заключается в отыскании параметров аналитической зависимости, которые минимизируют сумму квадратов отклонений эмпирических значений (реально полученных в ходе рангового анализа инфраструктуры образовательных учреждений) от значений, рассчитанных по аппроксимационной зависимости [2, 3, 5-7].

Листинг 3. Вычисление коэффициентов регрессии

T(W,r) — n ^ length(W)

P <

X ln(Wi)'^ ln(ri) - n-X (ln(Wi)'ln(ri))

i = 1 i = 1                i = 1

e

V i = ¹

) ^{2 ln} ( r i ⁾

J

n

- n - ^ (^( r i )) 2

i = 1

W1 ^ exp

1 n

'n

X

V i = 1

ln(Wi)+₽-X i=1

ln(ri)

J

WW ^ stack( p , W1)

WW

ню -	j ^ 1 while j < cols(V) + 1 Xj ^ z ( vj, r ) j ^ j +1 X

Входными аргументами функции T(W, r ) являются векторы параметрического распределения V (для одного временного интервала) и рангов R . Функция H(Z ) позволяет вычислить коэффициенты регрессии для всех распределений за рассматриваемый интервал времени.

Интервальное оценивание

Согласно принятым допущениям относительно значений электропотребления объектов, выходящих за пределы доверительного интервала, можно будет сделать следующие выводы. Если точка входит в доверительный интервал, то в пределах гауссового разброса параметров можно судить, что данный объект потребляет электроэнергию нормально для своего интервала разбиения рангового распределения. Если точка находится ниже доверительного интервала, то это, как правило, свидетельствует о нарушении нормального технологического процесса электропотребления на данном объекте (частые отключения электроэнергии, неплатежи, избыточная экономия и т.п.). Если точка находится выше интервала, то на соответствующем объекте имеет место аномально большое потребление электроэнергии. Именно на эти объекты в первую очередь должно нацеливаться углубленное энергетическое обследование (энергоаудит) [2,3].

Листинг 4. Линеаризация данных

В качестве исходных данных используются [4]: матрица коэффициентов регрессии coef := H(T) T;

вектор рангов объектов r := R;

количество объектов n := rows(M) = 49, i := 1..n;

вектор электропотребления, (кВт ⋅ ч),

Y := M где M := Zipf(W) - матрица табулированного рангового распределения электропотребления образовательных учреждений Нерюнгринского района за рассматриваемый временной интервал Time (в качестве примера рассмотрен Time := 6 - шестой временной интервал, что соответствует 2009 году).

Линеаризуем и логарифмируем векторы эмпирических данных Y по электропотреблению образовательных учреждений

Yl := ln( Y )

и ранговr rl := ln(r).

Создаем вектор единиц

Р, ^:= ¹

и объединяем его с вектором рангов r

X := augment( p , rl ).

Считываем коэффициенты регрессии, вычисленные методом наименьших квадратов для вектора электропотребления Y в := coef ттe, 1 = 1.21, Wl := coef t^, 2 = 1.976 • 106, и получаем уравнение аппроксимационной кривой [3,4] ym — ^^^

Листинг 5. Определение доверительного интервала распределения

Вычисляем остаточное среднее квадратическое отклонение

• ⁵ ^^ ^{1П(Ут 1 )) 1.729}

и коэффициент Стьюдента [4, 5]

t-₉t(l-₅ ^ ,_n- 3) = 1.679.

Рассчитываем ковариационную матрицу для линеаризованной модели: г т УЛ-1 - ( 0.25   -0.078А    п - v г ^_nvT

С-⁽Х •Х)  -(-0.078  0.02₆ ) D-X^C K-D^X .

т т                                                                  w

Извлекаем диагональные элементы из квадратной матрицы:

D(M) —

n ← rows(M)

for i ∈ 1 .. rows(M)

for j ∈ 1 .. rows(M)

W i ← M i , j if ij

W

V — D(K) Vl — VV

• Строим доверительные границы для расчетных данных (рис. 2):

> d — t • 5 • V

Y L — ln(ym)

Линейные верхняя yd 12 := YL + d и нижняя yd 11 := YL - d границы интервала.

Нелинейные верхняя yd 2:=exp( yd 12) и нижняя yd 1:=exp( yd 11) границы интервала (рис. 3).

Выявление объектов с аномальным электропотреблением

Определяем количество точек, находящихся выше и ниже доверительного интервала, а также попавших в него (рис. 3):

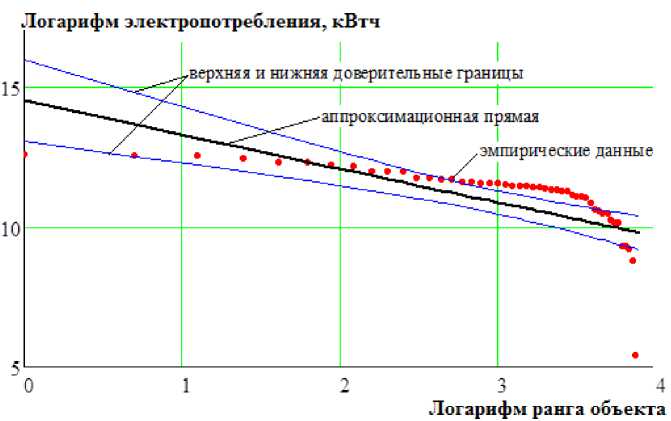
Рис. 2. Доверительный интервал для линеаризованного рангового параметрического распределения инфраструктуры образовательных учреждений (фрагмент)

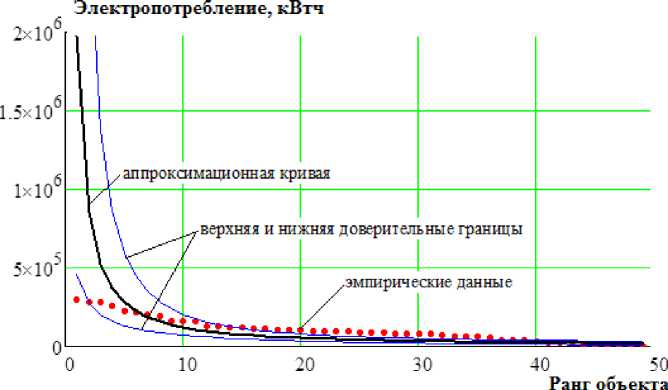
Рис. 3. Доверительный интервал для полного рангового параметрического распределения инфраструктуры образовательных учреждений

I i ^: if ⁽^ >  уй2ь ¹. if^^ i > ydl i , 1, 0)).

В итоге количество образовательных учреждений, имеющих аномально большое потребление электроэнергии, составило Σ _i [ I_i ∙ ( I_i > 0)] = 22, количество образовательных учреждений, имеющих нормальное потребление электроэнергии, составило IN := Е i ( f = 0) = 20 и количество образовательных учреждений, имеющих необоснованно низкое потребление электроэнергии, составило |Σ i [ I i ∙ ( I i < 0)]| = 7.

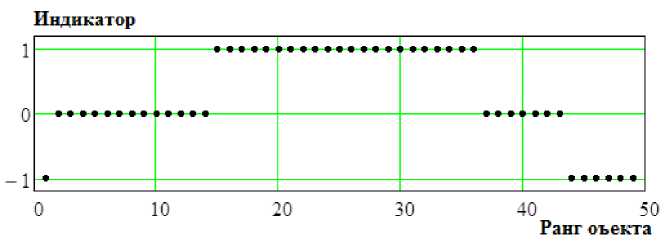
Рис. 4. График, иллюстрирующий попадание точек в доверительный интервал. Индикатор принимает значение 0, 1 или -1, если точки лежат внутри, выше или ниже доверительного интервала соответственно

Листинг 6. Получение списка очередности проведения энергоаудита

Определяем относительную величину отклонения точек от границ доверительного интервала, а затем ранжируем объекты по данному параметру.

,    Y;>yd^2^ yd2i’lf Yi

OTN - (Q^ym^-1) OTNM - |OT^|

R(a,r) —

c ← sort(a) b ← reverse(c) for m ∈1 .. rows(a) for n∈1.. rows(b) n ← rm   am   n L

SPR^-R(OTN^M, r⁾ns^-n^-IN = 29 Ran^{- R} -^g

Получаем список рангов образовательных учреждений

SPRANG — submatrix(SPR, 1,ns, 1,1)

SPRANG⁷=

	1	2	3	4	5	6	7	8	9	10
1	31	30	29	28	26	34	27	25	32	...

Определяем номер объекта (столбца) в начальной базе данных по электропотреблению (созданная ранее в MS Excel матрица V).

Unrang(a,b) ^

L←0 i←1 for m ∈1 .. rows(a) for n ∈1 .. rows(b) Li← n if am bn Li " i +1

В итоге получаем список очередности аудита образовательных учреждений Нерюнгрин-ского района (в результирующем векторе указан их номер в исходной базе данных):

	1	2	3	4	5	6	7	8	9	10	11	12	13
1	19	14	47	40	28	34	38	41	20	12	15	10	...

Таким образом, первые три объекта из списка, имеющие номера 19, 14, 47, требующие первоочередного энергетического обследования, соответственно: «Снежинка» Д/с ЦРР № 3, «Энергетик» Д/с КВ № 48, МОУ ДОД Детская музыкальная школа. Остальные легко определяются по полученному списку.

Вывод

Последовательная реализация данного способа (на протяжении ряда лет) позволит каждый раз выявлять и целенаправленно воздействовать на наиболее «слабые» объекты инфраструктуры образовательных учреждений Нерюнгринского района. При этом средства на проведение энергетических обследований будут расходоваться наиболее эффективно, а общее электропотребление образовательных учреждений будет постоянно снижаться.

Siberian Federal University

79, Svobodniy, Krasnoyarsk, 660041 Russia Northeast federal university M.K.Ammosov’s name 16 Kravchenko Str., Nerungry, 678960 Russia

The method of determining of priority energy inspection(energy audit) for object with irrational power consumption founded on interval estimation of parametric rank distributon is examined. Using this method will allow to discover and purposive act on the most “weak” objects goverment-financed organizations and offices of munitipal level. The method is realzed in MathCAD program and presented for infrastructure of educational institutions of Nerungry district.