Способ проверки корректности планировщика задач операционной системы реального времени с помощью сетей Петри

Одной из основных систем управления современной бортовой аппаратурой (далее – БА) космических аппаратов (далее – КА) является система реального времени (далее – СРВ). В системах данного типа [1; 2] важна не только логическая корректность вычислений, но и временной интервал, в течение которого будет достигнут результат. Такая система гарантирует своевременную реакцию на внешние воздействия, что повышает устойчивость работы системы управления бортовой аппаратуры.

Операционные системы реального времени (далее – ОСРВ) позволяют решить ряд важных задач (например, задачи системы ориентирования или энергообеспечения КА) в заданные требованиями промежутки времени. При этом выполнение задачи в ограниченный промежуток времени, а также гарантированное время отклика задачи обеспечивают надежное функционирование КА. Решение поставленной цели может быть выполнено с помощью планировщика, представляющего собой программное обеспечение ОСРВ и предназначенного для управления задачами.

Применение планировщика задач позволяет системам реального времени достичь выполнения следующих качественных характеристик: справедливость, предсказуемость и баланс производительности. Для ранней проверки корректности алгоритмов планирования задач операционных систем реального времени, в зависимости от конфигурации целевой системы и временных ограничений необходимо применение современных научных методов выявления ошибок.

В данной статье представлено решение задачи проверки корректности планировщика задач операционной системы реального времени с применением временных сетей Петри – одной из формальных моделей, используемых при верификации проекта операционной системы реального времени бортовой аппаратуры малого космического аппарата.

Целью исследования является разработка способа проверки корректности функционирования планировщика задач операционной системы реального времени при различных аппаратных конфигурациях вычислительных систем бортового оборудования.

Моделирование приложения реального времени

В качестве формальной модели корректности работы планировщика задач операционной системы реального времени используется модель временной сети Петри. Исходными данными для планирования задач являются необходимые процессы, функционирующие в системе реального времени и их приоритеты [3].

Обычно работа алгоритма планировщика происходит на временном интервале (0, t), который в каждый момент времени определяет количество задач, находящихся в состоянии готовности. В случае наличия одной готовой задачи она исполняется согласно своему приоритету, либо завершается один из ее фрагментов после того, как была завершена более приоритетная задача [4; 5].

Планировать задачи в системе реального времени можно статическими и динамическими методами. В качестве политики планировщика со статическими приоритетами используется алгоритм RMS (Rate Monotonic Scheduling – планирование с монотонной скоростью). Статические приоритеты назначаются задачам в соответствии с продолжительностью цикла задания, поэтому наиболее короткая продолжительность цикла приводит к более высокому приоритету задачи.

В случае применения планировщиком алгоритма EDF (Earliest Deadline First – первоочередное планирование более раннего срока выполнения) используется динамический принцип назначения приоритетов задачам. Планировщик задач, построенный на данном алгоритме, считает, что чем ближе предельный срок выполнения задачи, тем ее приоритет выше.

При моделировании приложения реального времени представляются набором задач. Для планирования времени исполнения каждая задача обычно определяется следующими временными параметрами [6]:

C _i – время выполнения задачи в наихудшем случае (WCET – worst-case execution time);

P _i – период (продолжительность между двумя задачами);

D _i – критический срок завершения выполнения задачи;

U – коэффициент использования процессора.

Необходимое условие того, что система реального времени будет исполнимой, – коэффициент использования процессора должен быть меньше или равен 1 [6]:

• • по алгоритму RMS

	n U = 1 у                          (1)
• по алгоритму EDF	i = 1 i n U = ^ в                           (2)

В общем виде сеть Петри может быть представлена следующим выражением [7; 8]:

С = ( P, T, I, O), (3) где P = {p1,p2,...,pn} - конечное множество позиций; T = {t 1,t2,...,tm} - конечное множество переходов; I: T ^ P™ - входная функция (отображение из переходов во входные комплекты позиций); O: T ^ Р^ - выходная функция (отображение из переходов в выходные комплекты позиций).

Маркировкой ^ сети Петри называется функция, отображающая множество позиций P в множество неотрицательных целых чисел N [9; 10].

Активные переходы t j е T в маркированной сети Петри с заданной маркировкой ^ разрешены, если для всех p i е Р выполняется следующее условие:

^ ( P i ) ^ # ( P i , I ( t j ) ) ,

Способ проверки корректности планировщика задач операционной системы ...

где # - оператор кратности перехода; p i е P - множество разрешённых позиций; t j е T - множество активных переходов.

В классической модели сети Петри отсутствует понятие времени. В то же время в асинхронных системах события могут происходить в неопределенных временных интервалах, что затрудняет указание точного времени длительности таких событий или их начала и окончания. Для преодоления указанных ограничений используются расширения сети Петри – временные сети Петри с возможностью задания времени переходов и задержки маркеров в позициях сети.

В качестве модели каждой выполняемой задачи в ОСРВ можно использовать следующий кортеж переходов временной сети Петри:

Task = ( c i , r i , s i , e i , d i ) ,                                                (5)

где ci – периодически создает маркер нового экземпляра задачи; ri – отмечает маркер задачи как подготовленный, то есть задача готова к исполнению и ожидает запуска; si – за- пускает задачу, меняет ее состояние с «ожидание» на «выполнение»; ei – завершает выполнение задачи, освобождает общие ресурсы и отмечает ее состояние как «выполне- на»; di - переход deadline_task происходит, когда задача все еще выполняется и создан ее новый экземпляр.

В качестве примера системы ограничений рассмотрим модель ОСРВ с двумя задача- ми – Taski и Task j – с более высоким приоритетом задачи Taski . Тогда для проверки корректности планирования задач можно использовать следующую систему ограничений:

⁽ c i , r i , s i ) > ⁽ c j , r j , s j ) ,

VV(Pi )^((Pdeadline^k )^ 1; Vе R(C, (), где Pdeadiine task - позиция максимального срока выполнения задачи Taski; > - отношение приоритета выполняемых задач; R – множество достижимости сети Петри.

С применением математической постановки задачи разработан алгоритм проверки корректности функционирования планировщика задач операционной системы реального времени с применением временных сетей Петри.

Алгоритм проверки корректности функционирования планировщика задач ОСРВ

На основе вышеизложенного в статье представлен способ проверки корректности расписания задач планировщика операционной системы реального времени.

Планирование задач в ОСРВ производится с целью установления детерминированных гарантий как выполнения необходимых задач, так и требуемого времени их отклика. Алгоритм проверки корректности функционирования планировщика задач представлен на Рисунке 1 и предназначен для моделирования функционирования задач со статическими приоритетами в операционной системе реального времени.

При построении алгоритма планировщика задач ОСРВ используется метод RMS [4]. Статические приоритеты задач назначаются в соответствии с продолжительностью цикла задачи Taski .

В исходных ограничениях моделируемых задач ОСРВ указывается их общее количество, временные ограничения, статические приоритеты. Далее, исходя из выбранной модели исполняемой задачи, формируется временная сеть Петри для заданной группы задач ОСРВ (в примере используются задачи с приоритетами 5 и 11, общее время выполнения каждой из задач составляет 2 мкс).

Для проверки корректности работы планировщика была выбрана программная среда моделирования сетей Петри TINA [11–13]. Данная среда предназначена для визуального моделирования сетей Петри (в том числе с временными ограничениями), динамического исполнения моделей сетей, проведения проверки заданных ограничений для выбранной сети Петри.

С учетом вышеизложенного разработана модель временной сети Петри для ОСРВ с заданным количеством задач и их временными характеристиками. Общий вид данной модели в программной среде представлен на Рисунке 2.

По алгоритму проверки корректности планировщика производится запуск на выполнение разработанной модели временной сети Петри. На Рисунке 2 отображен процесс функционирования системы с двумя задачами при установленных ограничениях. Программная среда выдает отчеты об ошибках в реальном масштабе времени. При необходимости производится настройка количества шагов выполнения спроектированной модели.

При этом для тестируемой модели сделано допущение выполнения задач на одном процессоре. По результатам исследования было установлено, что в случае увеличения общего времени выполнения задач до 4 мкс планировщик не сможет гарантировать их своевременного запуска.

В случае реализации ОСРВ для малых космических аппаратов дополнительно необходимо учитывать ограничения аппаратной платформы. Обычной компоновкой таких решений является реализация вычислительной системы, использующей ресурсы микропроцессорного ядра, интегрированного в один кристалл совместно с устройствами ввода/ вывода.

Способ проверки корректности планировщика задач операционной системы ...

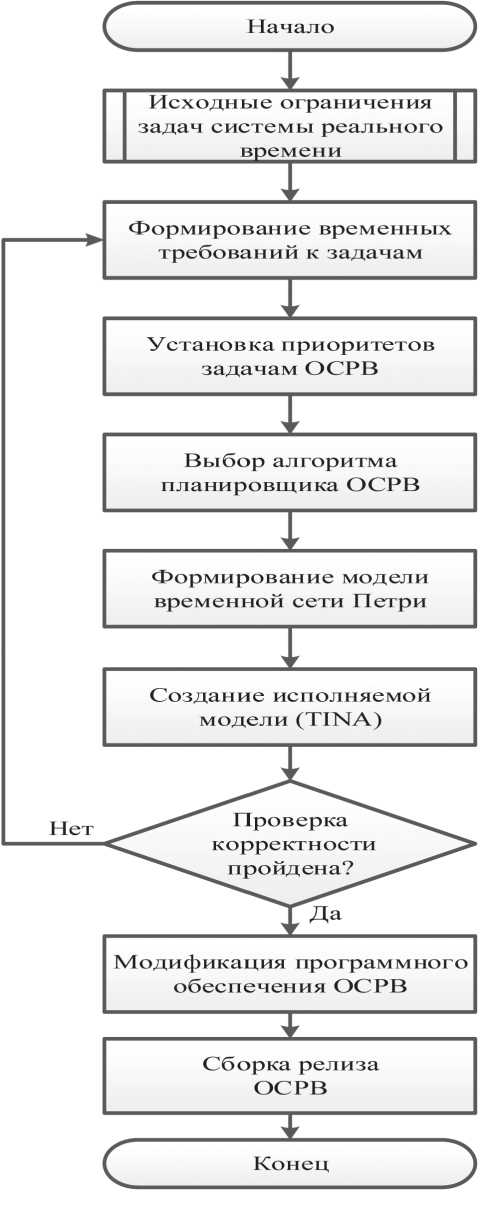
Рисунок 1. Алгоритм проверки корректности функционирования планировщика задач ОСРВ с применением сетей Петри Источник: рисунки выполнены авторами.

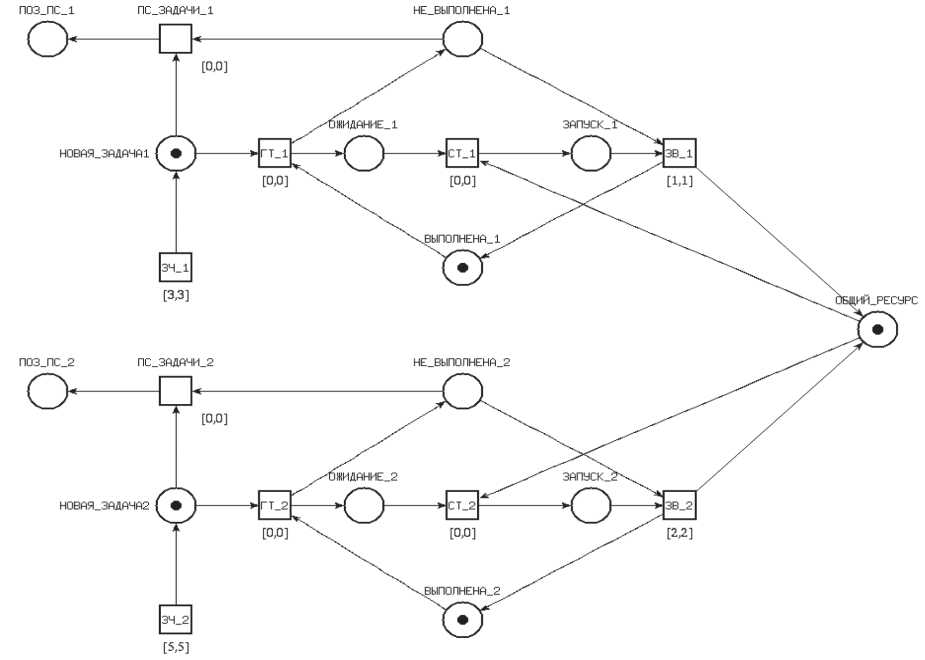
Рисунок 2. Модель планировщика ОСРВ с двумя задачами

Главной особенностью ОСРВ для встроенных решений является компактность исполнения при реализации быстрой реакции на внешние события и развитых средств межпроцессного взаимодействия.

В Таблице представлены технические параметры ОСРВ для микроконтроллерных платформ [14; 15].

Таблица

Технические параметры ОСРВ для различных платформ

Наименование и версия ОСРВ	Поддерживаемые аппаратные платформы	Макс. кол-во задач	Кол-во приори-тетов	Размер памяти, байт		Реализация алгоритмов планировщика
				Задача	Планировщик
Zephyr OS 3.5.0	ARM, Intel x86, ARC,SPARC, RISC-V, MIPS, Xtensa	3-20	32	256-2048	512-2048	RMS,EDF, Round-Robin, Time-Slice
FreeRTOS 10.0.1	ARM, Intel x86, PIC, AVR		7	128-3072		RMS,EDF, Round-Robin
CoOS 1.1.6	ARM, Intel x86	5	64	68	168-1142	RMS,EDF, Round-Robin

Источник: [14; 15].

Способ проверки корректности планировщика задач операционной системы ...

Указанные в Таблице аппаратные ограничения должны дополнительно учитываться при реализации бортовых вычислительных малых космических аппаратов.

Из анализа полученных результатов следует, что в случае увеличения времени выполнения задачи до 4 мкс невозможно составить корректное расписание планировщика вычислительной системы бортовой аппаратуры, что потенциально может привести к срыву выполнения задачи управления аппаратом (задачи управления ориентацией космического аппарата критично важны для его надежного функционирования). Отдельно необходимо отметить аппаратные ограничения микроконтроллерных платформ, наиболее часто используемых для построения вычислительных систем малых космических аппаратов.

Оценки планирования потоков исполнения могут основываться на временных измерениях кода прототипа или данных для аналогичного проекта (например, системы с одинаковыми реализациями ОСРВ и аппаратными ограничениями). Проводя анализ на ранней стадии процесса разработки с использованием модели временной сети Петри, можно получить качественные прогнозы функционирования планировщика задач.

Заключение

Таким образом, для проведения проверки корректности планирования задач ОСРВ, используемых при функционировании бортовой аппаратуры КА, необходимо применение разработанного алгоритма, позволяющего проводить верификацию планировщика задач ОСРВ БА КА с использованием моделей временных сетей Петри.

Применение научно-методического аппарата временных сетей Петри позволяет проводить верификацию различных задач ОСРВ, выполняемых в БА КА.

В данной статье рассмотрен способ проверки корректности функционирования планировщика задач операционной системы реального времени с применением сетей Петри. Представленный способ основан на применении моделей временных сетей Петри.

Применение средств проверки корректности функционирования планировщика задач ОСРВ на основе временных сетей Петри позволит повысить качество программного обеспечения, используемого при создании БА КА.

Результаты проведенных исследований могут быть использованы при создании новых образцов космической техники и разработки процедур верификации проектов интегрированной бортовой аппаратуры КА.