Способ стабилизации мощности излучения лазера
Автор: Петропавловский Владимир Максимович, Топоркова Любовь Владимировна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии радиосвязи, радиовещания и телевидения
Статья в выпуске: 2 т.11, 2013 года.
Бесплатный доступ
Предложен способ стабилизации мощности излучения одномодового лазера на основе явления тепловой линзы. Рассчитаны зависимость мощности излучения на выходе стабилизатора от мощности излучения лазера и коэффициент стабилизации.
Стабилизация мощности лазера, тепловая линза
Короткий адрес: https://sciup.org/140191629
IDR: 140191629 | УДК: 621.375:
Текст научной статьи Способ стабилизации мощности излучения лазера
Введение. Постановка задачи
Для задач контроля качества оптических волокон и метрологии требуются лазеры с высокой долговременной стабильностью мощности излучения. Существующие методы затрагивают только стабилизацию электрической мощности блока питания. Между тем изменение параметров окружающей среды (прежде всего температуры)
приводит к изменению характеристик излучателя (например, за счет частичной разъюстировки), что ведет к уменьшению выходной мощности. В данной статье предлагается способ стабилизации мощности излучения лазера, основанный на явлении самодефокусировки лазерного пучка, проходящего через среду с отрицательной величиной ∂ n /∂ T .
Рис. 1. Принципиальная схема установки
Принципиальная схема установки приведена на рис. 1. Лазерный пучок фокусируется линзой 2 в кювету 3, содержащую жидкость (например, ацетон). Частичное поглощение излучения приводит к выделению тепла и росту температуры жидкости. Происходит изменение показателя преломления жидкости Δ n = ∂ n /∂ T ·Δ T . Так как распределение интенсивности по сечению лазерного пучка неоднородно, то и изменение показателя преломления в разных точках будет различным. В случае одномодового лазера вблизи оси пучка изменение показателя преломления происходит по квадратичному закону. Такая структура аналогична рассеивающей линзе (так как ∂ n /∂ T < 0). Расходимость пучка, проходящего через эту линзу, увеличивается, поэтому увеличивается и ширина распределения интенсивности (диаметр) пучка в дальней зоне. Подобрав диаметр пучка в перетяжке после линзы 2 – w0 , можно добиться постоянства интенсивности на оси пучка. Линза 4 коллимирует пучок, диафрагма 5 вырезает центральную часть пучка с постоянной мощностью.
Фокусноерасстояниетепловойлинзы
Разложим показатель преломления, распределение которого цилиндрически-симметрично, в ряд Макларена по радиальному смещению от оси:
/ x Г 611
Иф) = Иф) + Г —
V 6г r=0
Иби
2 6г1
+ ... (1)
/■=0
Для цилиндрически-симметричного распределения (∂ n ∂ r ) r = 0 = 0. Луч, входящий в среду параллельно оси симметрии, будет идти по кривой, радиус кривизны которой рассчитан в [1] как
— = v • grad [in п ]
где v – единичный вектор главной нормали к кривой. Предполагая, что градиент направлен по радиусу и что среда тонкая, (2) можно преобразовать к виду
1 = ^^. (3)
R и 6г1
Эффективное фокусное расстояние среды длиной L связано с радиусом кривизны луча R , вошедшего в среду на расстоянии r от оси симметрии
1 _ nL _ б1^
F rR v6r vг
Радиальное распределение показателя преломления можно выразить через радиальное распределение температуры, получаем
1 _ L dn(dV f” diver1,
то есть оптическая сила тепловой линзы зависит от распределения температуры в среде. В подавляющем большинстве сред ( dn / dT ) и (∂2 n /∂ r 2) r = 0 отрицательны, так что тепловая линза рассеивает свет ( F < 0).
Распределение температуры в среде
Функция, описывающая температуру в бесконечной цилиндрически-симметричной среде, в которой в момент времени t = 0 в бесконечномалом элементе цилиндра радиуса r ´ мгновенно выделилась тепловая энергия [2]:
G(r,r',t) =
Q ^TrDt
( r^r'A exp--
^Dt
rr
(6) ,
D = k /( ρcp ) – коэффициент температуропроводности; k – коэффициент теплопроводности; cp – удельная теплоемкость; ρ – плотность; 7o(") – модифицированная функция Бесселя; Q – интенсивность теплового импульса на единицу длины (скачок температуры, возникающий за счет выделения тепла). В случае, если источник тепла действует непрерывно (непрерывный лазер), температура на расстоянии r от оси в момент времени t вычисляется как результат интегрирования (6) по временам t ´, лежащим в интервале 0 ≤ t ´ ≤ t . В этом случае вместо количества мгновенно выделившейся тепловой энергии вводится скорость выделения тепла на единицу длины Q = al . Поэтому (6) можно переписать в виде:
. , , Inr'QIpcn
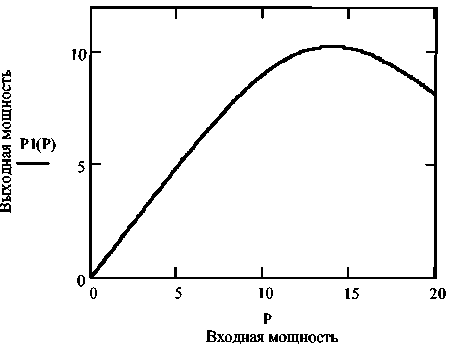
G AirDt x exp W В случае одномодового лазера с гауссовым профилем распределения интенсивности по сечению пучка рост температуры может быть найден как T(r,t) = jdf jdr’ о 0 2 л" r' -----exp ^dz' (f2 + f'2 W 2;rkw2 27rkw2 •(12) В этой формуле предполагается постоянство радиуса лазерного пучка w вдоль длины кюветы, то есть длина кюветы L должна быть меньше кон- TTW" фокального параметра пучка ^0 — ’ λ – длина волны излучения. Найдем теперь вторую производную температуры по радиусу при r = 0 и вычислим, используя (5) фокусное расстояние тепловой линзы. Интегрирование (8) по r´ дает: Изменение диаметра пучка в дальней зоне. Мощность излучения на выходе стабилизатора Для гауссового пучка с радиусом перетяжки w0 радиус пучка W на экране в дальней зоне (расстояние до перетяжки - » —Г" = b0 ) может быть найден как ^0 2 л-r' -----exp 4л Dt' Если такой пучок с исходной мощностью Р пропустить через диафрагму радиусом а, то мощность пучка после диафрагмы будет aP л w2 aP тгк exp w2 + W —-.------- exp - w-^W Px = P 1 - exp - ^y Вычислить вторую производную по r проще до интегрирования по времени. Получим Прохождение пучка через линзу приводит к изменению радиуса кривизны волнового фронта R. Размер и положение перетяжки нового пучка меняются, следовательно, изменятся W и P1. Для расчета параметров нового пучка воспользуем- a2( aP dr2 ^k D w2 + ^Dt' w2+Wt' ся формализмом комплексного параметра пуч-1 IX Л ка q vq R ttw2 В перетяжке q – мнимый 4aPD ^гк^Т%5?^' _ ITTWq I I n q —~ • При распространении в среде длиной x q меняется по закону q2 = q1 + x. При прохож- Вычисление интеграла по t´ дает 0-T _ 7 4aPD a?-2 “J Tikkw-*%nt'Y aP 2^kw2(\ + tc / 2?) дении через линзу радиус кривизны волнового фронта меняется по закону r F То есть если отрицательная линза помещена в перетяжку пучка, то после линзы будет расходящийся пучок с R = F. В результате получим уравнение Параметр tc = w2/4D характеризует временной отклик среды на выделение тепла (время установления теплового равновесия). Подстановка (11) в (5) дает 1 _ IX 1 l4- 7TVg ’ 2 Г Л’И'д где х – расстояние до новой перетяжки; v0 – ее размер. Решая (15) получим F^ = - 2л к w2 (1 + tc / 21) при условии t >> tc: Размер пучка на экране станет W1: ^ =я(2+^ ^v0 Подстановка (12), (15) и (16) в (14) дает Р^Р) = Р<Л - exp w\P> ; (18) «р-р l + ^/C,)2 Построенный по формуле (18) график зависимости мощности излучения на выходе из стабилизатора от мощности излучения лазера приведен на рис. 2. Рис. 2. Зависимость мощности излучения на выходе из стабилизатора от мощности излучения лазера Как видно из рис. 2, функция P1(P) имеет максимум вблизи Р = 14 мВт. При изменении Р на величину ±1,5 мВт выходная мощность P1 меняется не более чем на 0,17 мВт, что означает повыше- ние стабильности в 17 раз. Увеличение стабильности мощности входного излучения приведет к еще большим значениям коэффициента стабилизации. Таким образом, мы показали, что на основе эффекта тепловой линзы может быть создано устройство, стабилизирующее мощность излучения непрерывного лазера. К недостаткам метода можно отнести уменьшение мощности (в рассмотренном примере почти в 1,5 раза) и невысокое быстродействие (~1 мс). Увеличение размера диафрагмы а приведет к увеличению выходной мощности, но и к снижению коэффициента стабилизации установки ΔР/ΔР1. При необходимости повышения коэффициента стабилизации нужно уменьшить диаметр диафрагмы. К преимуществам метода относится простота конструкции стабилизатора и отсутствие внешних управляющих устройств. Подбор рабочей точки для требуемой величины выходной мощности и (или) коэффициента стабилизации осуществляется путем изменения диаметра диафрагмы, поглощения жидкости, длины кюветы или размера перетяжки.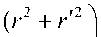
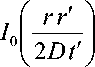
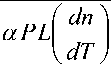
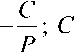
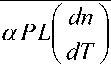
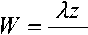
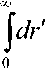
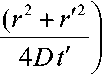
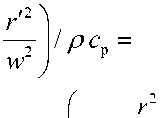
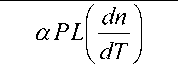

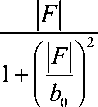
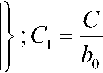
Список литературы Способ стабилизации мощности излучения лазера
- Борн М., Вольф Э. Основы оптики. М.: Наука, 1970. -720 с.
- Карлсроу Х.С., Егер Д. Операционные методы в прикладной математике. М.: ИЛ, 1948. -624 с.
- Hansen K.R. єл. Thermo-optical effects in highpower ytterbium-doped fiber amplifiers//Opt. Express. V19, N24, 2011. -P. 23965-23980.
- E. Wyss e.a. Thermooptical compensation methods for high-power lasers//IEEE J. Quantum Electron. V.38, N12, 2002. -P. 1620-1628.


