Способ терминального управления на участке выведения беспилотного летательного аппарата с баллистической фазой полета

УДК 62-50                                                  

Введение. В настоящее время возможности и сфера применения беспилотных летательных аппаратов (БЛА) существенно возросли. В первую очередь это связано с увеличением дальностью полета БЛА. В аппаратах с баллистической фазой полета необходимо предусмотреть возможность управления на различных участках, в том числе на разгонном участке выведения БЛА в заданную область. Для формирования управления целесообразно использовать принцип терминального наведения. При этом управление должно формироваться как функция конечных параметров движения, а не функция времени.

Решению этой проблемы посвящены многие публикации, однако описанная выше задача сохраняет актуальность. В частности, представляет интерес разработка высокоэффективных в вычислительном отношении алгоритмических способов терминального наведения. При этом следует учитывать указанные особенности, универсальные для различных типов средств выведения. Они обладают свойствами адаптации и в определенном смысле удовлетворяют требованиям оптимальности.

С точки зрения задачи наведения особый смысл имеет такое управление, при котором используется минимальное количество топлива. Синтез оптимального управления базируется на применении метода динамического программирования Беллмана [1].

Материалы и методы. Решение задачи синтеза оптимального управления движением БЛА на разгонном участке активного полета исследовалось во многих работах. Однако полученное в большинстве случаев решение оптимального управления сводится к реализации временной или параметрической программы. Будем решать задачу поиска оптимального управления на участке выведения БЛА в следующей постановке. Известными являются параметры движения БЛА как координаты X 0 , Y 0 , Z 0 текущей точки траектории, получаемые за счет решения задачи навигации. Параметры конечной точки X _к , Y _к , Z _к удовлетворяют граничному состоянию, фиксирующему переход к баллистической фазе полета, определяемой гиперповерхностью в фазовом пространстве. Условию S k ( X _к , Y _к , Z _к ) = 0 удовлетворяет целое множество конечных параметров. Требуется синтезировать оптимальное управление в задаче наведения БЛА, которая обеспечивает его перевод из начального состояния на гиперповерхность конечных условий.

В качестве критерия оптимальности принимается количество израсходованного на разгонном участке топлива:

m ( t ) = j m ( t ) dt ,                                                     (1)

0 где m ( t ) — секундовый массовый расход топлива.

В качестве математической модели движения центра масс принимается следующая система дифференциальных уравнений:

R(t) = V(t),                                                     (2)

V (t) = W (t) Ew, (t) + g (r ), где R(t) — радиус-вектор, g(r) — вектор силы притяжения Земли, W(t) — модуль вектора управляющего ускорения.

Модуль вектора управляющего ускорения W(t) является заданной функцией времени и определяется характеристиками двигателя БЛА. Неизвестным является единичный вектор управляющего ускорения Ew (t). При решении задачи оптимизации он будет определять требуемые свойства управляемого движения БЛА на разгонном участке. Нет необходимости в регулировании величины вектора тяги (в известном смысле это величина кажущегося ускорения W(t)). Более рациональный подход — максимизация этой величины для применя- емого на разгонной ступени носителя двигателя. Это позволяет применить полученные решения и для случая использования твердотопливных двигателей. Характеристики двигателя БЛА являются достаточно стабильными, и при постоянном секундном расходе топлива m(t) = const оптимальность управления определяется продолжительностью активного участка полета. В этом случае функционал (1) будет функцией верхнего предела интегрирования. Таким образом, задача минимизации количества топлива превращается в эквивалентную задачу минимизации продолжительности полета, а критерием оптимальности будет быстродействие. Задача синтеза заключается в нахождении ориентации вектора тяги двигателя БЛА, которая определяется направляющими косинусами вектора тяги P(t) как функции текущих параметров и конечного состояния.

Сделаем два допущения. Первое. Поскольку большая часть разгонного участка лежит за пределами плотных слоев атмосферы, не будем учитывать как ограничение угловую скорость изменения вектора тяги в пространстве (продольной оси БЛА). Второе. Движение БЛА будем считать проходящим в определяемой зара- нее плоскости.

Конечное состояние БЛА для перехода к баллистической фазе полета фиксируется выполнением следующего граничного условия [2]:

5 y = ( V_xky_t-VyV_yk ) [ V , ( у_к-у— ) — V yk (.

—

- п ( v ² + у ² )^1/2

0 цц

.      ^VV ⁺ у к Уу

1/2      2 \^1/2 / 2      2

( ^V ц ⁺ У — )  ( ^Vk ⁺ Ук )

= 0.

Здесь xk,yk,x,y — соответственно координаты начальной точки и точки начала функционирования БЛА на заключительном участке траектории. Величина текущего значения граничного условия S1k (t0) является мерой невыполнения условия (3). Математическая запись этого условия соответствует гиперповерхности, которая является гладкой функцией фазовых координат и описывает все семейство возможных траекторий выведения БЛА [2].

Граничные условия заданы для центрального поля притяжения. Уравнения движения БЛА для этого случая будут иметь следующий вид:

• V 1 = V 2 ,

• ■ П . 1

v ₂ = —0 V 1 +— P cos а _1?

r ³      m

V 3 = v 4 ,

• . П . 1

v 4 = —0 v₃ + — P cos а ₂ .

r ³      m

Здесь п ₀ = f • M — постоянная центрального поля притяжения Земли, равная произведению гравитационной постоянной f на массу Земли М з ; r = ( V 2 + v ₃²)^1/2, V 1 = v , v 2 = V_v , v ₃ = у, v 4 = V_y ; P — величина вектора тяги; X A — аэродинамическая сила лобового сопротивления; Y А — аэродинамическая подъемная сила.

Поскольку БЛА снабжается двигателем с управляемым вектором тяги, то его ориентацию будут определять направляющие косинусы. В этом случае ограничение на управления будет определяться соотношением:

II P(t )|| = { [ P(t ) cos a , (t ) ] 2 + [ P(t ) cos a ₂ ( t ) ] 2}" < | P ⁰ ( t )| . (5)

Ограничение на управления (5) является «ограничением по гиперсфере». Из этого следует решение, при котором оптимальное управление не является кусочно-постоянным, без переключений. В этом случае оптимальная по быстродействию траектория выведения в фазовом пространстве не имеет «углов» и разрывов производной. Оптимальное по критерию быстродействия управление будет представлять собой нелинейную, непрерывную функцию граничных условий (3) [3].

Задача синтеза формулируется следующим образом. Объект управления из произвольного текущего состояния, принимаемого за начальное и определяемого текущим значением S 1 k в момент t 0 , переводится на гиперповерхность граничного условия S 1 k = 0 в момент t k . При этом учитывается ограничение на величину

Информатика, вычислительная техника и управление

управляющего ускорения (модуля тяги двигателя). Требуется найти оптимальное управление в форме синтеза, которое обеспечивает такой перевод за минимальное время.

Состояние объекта в конечный момент удовлетворяет граничному условию S ik [ X ( t_k )] = 0 и определяет момент перехода к баллистической фазе полета.

В соответствии с принципом динамического программирования Р. Беллмана [4] необходимым и достаточным условием оптимальности для сформулированной задачи будет соотношение:

min u e U

- д T0

Ё^ ^⁽ x , u ) i = 1 д x

i

- 1.

С учетом математической модели объекта, заданной системой (4), уравнение динамического программирования [4] с учетом критерия оптимальности определяется соотношением min ueU

_ ( ^П 0 --- д x  I

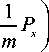
д T ⁰      д T ⁰

----+ x4---- д x 2       д x 3

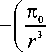
1 P ) д T° m y J д x 4

—1,

где P _x = P cos a ₁ , P y = P cos a ₂ .

В соответствии с методологией динамического программирования Р. Беллмана, операция минимизации может быть проведена на основе применения к соотношению (5) неравенства Шварца [3]. Это позволит существенно упростить решение задачи оптимизации. Тогда выражение (7) с учетом неравенства (5) будет определяться соотношением

1 д T ⁰ Y ( 1 д T ⁰ —I ⁺ l —— m д x ₂ J ( m д x ₄

min ( 1 P x дЛ+ 1 p дЛ L p o_{( t} ) ^{u e U} ( m   д x ₂ m y д x 4 J

В этом случае уравнение Гамильтона — Якоби будет представлено так:

x ₂

1 д T ⁰ Y ² ( 1 д T ⁰ —;— I ⁺ l —;— m ^{д x} 2 J ( ^m 8 ^x 4

P ⁰ ( t )

= — 1.

X

Уравнение (9) решается с учетом заданного граничного условия:

^{T 0(} x„ x 2 , x 3 , x 4 ) = 0, при

⁽ x„ x 2 , x 3 , x 4 ) ^e S '.

Вычисление частных производных величины S по фазовым переменным x1,x2,x3,x4 дает следующие зависимости:

8 S^o                                2

- x 4 x 1 ц ) ,

—— = ( — 2 x ₂ x ₃ x ₄ + x ₂ x ₄ x _3|( + 2 x 4 x 1

д S⁰_{H 2}

= 2 x3 x, дx 2    V   32

дS0  H2

= 2 xx, дx 3    V   23

дS0  H2

— = ( ² x 1 x 4 д x 4

— 2 xx 4 x 3

— 2 x 2 x 4 x 1

— 2 x 1 x ₂ x ₃

- ² x 2 x 3 x 3ц

—

x 2 x 23ц

+ x.x.x, + x.x,x   ,

143 ц 431 ц ,

^— x 2 x 4 x , ) ,

+ 2 x.x.x. + x,xx + x_?x₃x  .

411ц   233 ц 231 ц

Подставляя соотношения (11) в (9) и выполняя несложные преобразования, получаем зависимость:

с граничными условиями

ме:

П.

^{ r^{( x} 1 ^{— x} 3 ) ^{— 2 x} 2 x 4 ^x 1 ц r ³

P ⁰

--X

m

^X[ ( ^{2 x} 3 ^{2 x} 2 — ^{2 x} 1 x 4 ^x 3 ^{— 2 x} 2 ^x 3 x 3ц ^{+ x} 1 x 4 x 3 ц ⁺ x 4 x 3 x 1 ц ) ^{2 +}

2      д T 0

:x 2 x. — 2 x.x.x, + 2 x.x. x. + x_?x₃x₃ + x,x,x. ) ] }---- = — 1

1 4    123    41 1ц   233 ц 231 ц S

T ⁰ ( S J = 0, при (^, x 2 , x 3 , x 4 ) e S*^.                                          ⁽13)

Выражение в фигурных скобках в (12), обозначенное через S '( x i ), можно записать в компактной фор-

S ' ( x. ) • — = - 1.

i    d S 1

Уравнение (14) с граничными условиями (13) можно решить различными способами, например методом характеристик [5]. Однако более рационально использовать следующую методику.

Выражение (11) определяет структуру оптимального управления [6]:

P opt ( x ) = - PE опт (x ), W опт ( x ) = - WE опт ( x ),

где E ( x ) — единичный вектор тяги.

Соотношение (15) в скалярном виде:

Popt = P cos a1, P;pt = Pcos a2, cos a1

cos a 2

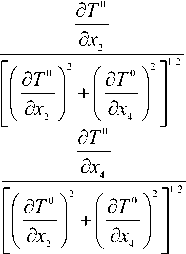
Уравнение (9) и соотношения (17) могут быть преобразованы к более удобному виду по следующим соображениям. Исходя из условий формирования множества возмущенных траекторий, за счет варьирования управления можно построить в фазовом пространстве гиперповерхность с равным временем выведения, то есть изохронную поверхность. Действительно, для каждой из точек фазовой траектории будем вычислять значение критерия оптимальности: J ( t ₁), J ( t ₂) , … , J ( t_k ).

Таким образом, получим совокупность траекторий для каждого t е [ t _H ,t k ] . В силу непрерывности зависимости x ( t ) и J от изменяемого управления, множество траекторий образует поверхность в фазовом пространстве X . Эта граничная поверхность, образованная множеством векторов x [ t i ,J ( t i )], является выпуклой и гладкой. Для условий перехода к баллистической фазе полета изохронная поверхность имеет точку касания с гиперповерхностью граничных условий.

При качественной реализации оптимального управления будет уменьшаться расстояние в фазовом пространстве между гиперповерхностью граничных условий S k = 0 и изохронной поверхностью T ( x , R _ц , t ) = 0. В некоторое время у двух поверхностей окажется общая точка (рис. 1).

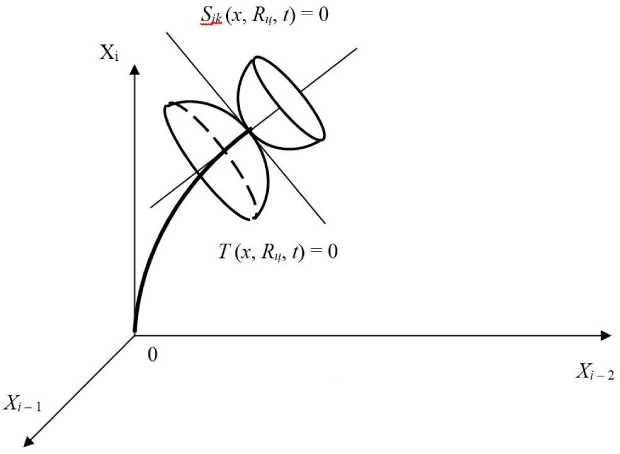
Рис. 1. Геометрическая интерпретация гиперповерхностей в фазовом пространстве при наведении на разгонном участке траектории

Информатика, вычислительная техника и управление

В точке S k и T 0 они имеют общую касательную, то есть их градиенты в фазовом пространстве совпадают. Таким образом:

• —    отмечается существование оптимальной траектории x opt ( t ) и оптимального управления u opt ( t );

• —    определяется окончание разгонного участка траектории ( t = t k ) и переход к баллистической фазе полета .

В точке касания изохронная поверхность и гиперповерхность граничных условий имеют общую касательную и нормаль. Математически условие существования общей нормали определяется выражением [2]:

[ d T 0 1 J dS.,, 1

^         A ^ -rk ^

I ^d x I ^d x

где А — константа, определяемая из анализа выпуклости обеих гиперповерхностей.

На основании соотношений (11) и (18) преобразуем (17). Получим выражение для направляющих косинусов вектора тяги в функции текущих и конечных параметров движения:

A =

[ ( —2x

( - 2 x 2 x з x 4 + x 2 x 4 x з ц + 2 x 2 X - x 2 X ^ )

22 , ₂x.x. + x.x.x. + 2 x. ² x - x. ² x    + 2 x.x ² - 2 xxx + 2 x.x.x. + x.x.x. + x.x.x    I ^1/2

234  243 ц 41  41 ц 41    123    141 ц 233 ц 231 ц

B =----

[ ( -2x

( ² xx 4 ^{- 2} x 2 x i x з + ² x 4 x ^ + x 2 x з x з ц + x 2 x з x ^ )

,x.x. + x.x.x. + 2 x. ² x - x. ² x    + 2 x.x ² - 2 x.x.x, + 2 x.x.x. + x.x.x, + x.x.x.

234  243 ц 41  41 ц 41    123   141 ц 233 ц 231 ц

где A = cos a 1 , B = cos a ₂ .

Из соотношений (19), (20) легко получить естественный для данного типа БЛА параметр для определения ориентации вектора управляющего ускорения (в известном смысле вектора тяги) — угол тангажа:

COS a₂    ( ² x 1 ^{2 x} 4 - ^{2 x} 2 x 1 x 3 ^{+ 2 x} 4 ^x ixm ^{+ x} 2 ^x 3 ^x 3 ц ^{+ x} 2 x 3 x 1 ц )

9 ( S ) = arctg----²- = ---—--------------—----₂—г--- .                  ⁽² 1)

^{cos a} i          ( ^{-2 x} 2 ^x 3 ^x 4 + ^x 2 ^x 4 ^x 3 ц + ^{2 x} 4 ^x i ^{- x} 4 ^xi₄ )

В нашем случае движение БЛА проходит в заданной плоскости и угол рыскания ф ( S ) = 0 . С использованием предложенной методики синтеза терминального оптимального управления был разработан алгоритм расчета угла тангажа [2] и проведено моделирование полета БЛА на ЭВМ [7].

Результаты исследования. Численные исследования проводились с использованием программного обеспечения, реализующего предложенный способ. Речь идет об алгоритмическом программном обеспечении терминального наведения баллистических летательных аппаратов на основе решения краевых задач баллистики. Соответствующая программа для ЭВМ зарегистрирована в 2013 году.

При моделировании использовалось гипотетическое разгонное средство с характеристиками и начальными условиями выведения БЛА, приведенными в [8].

Начальные условия при моделировании и результаты расчетов начального участка приведены в табл. 1.

Начальные условия выведения БЛА

Таблица 1

t	x/vx	y/vy	z/vz	wx/tang	wy/tet	w1/alf
0,0000	0,0	0,0	0,0	0,0000	0,0000	0,0000
	5,6323	–0,0000	322,6757	90,00	0,00	0,000
0,5537	3,1	3,1	178,7	–0,0000	16,6000	16,6000
	5,6323	11,1626	322,6756	90,00	1,98	–0,048
3,4580	34,7	120,9	1115,8	15,8242	103,4286	105,3386
	21,4565	69,4705	322,6727	69,34	12,13	–7,881
13,0193	832,4	1683,4	4200,8	150,0000	386,9131	419,3209
	155,6274	259,0827	322,6335	60,00	35,91	0,011
23,0193	3384,5	5300,4	7426,8	362,7748	690,8797	790,8281
	368,3725	464,9493	322,5441	50,02	43,59	–2,076
33,0193	8469,9	11009,1	10651,6	656,7462	1003,1187	1219,9140
	662,2567	679,2317	322,4053	43,44	42,79	–2,582
43,0193	16923,8	18956,0	13874,7	1039,4134	1336,7768	1727,7590
	1044,7345	915,1428	322,2176	38,74	40,11	–2,677
50,9898	26729,1	27089,4	16442,2	1424,0909	1630,6058	2211,8627
	1429,1498	1131,2610	322,0334	36,01	37,94	–2,501

График изменения угла тангажа на разгонном участке полета показан на рис. 2.

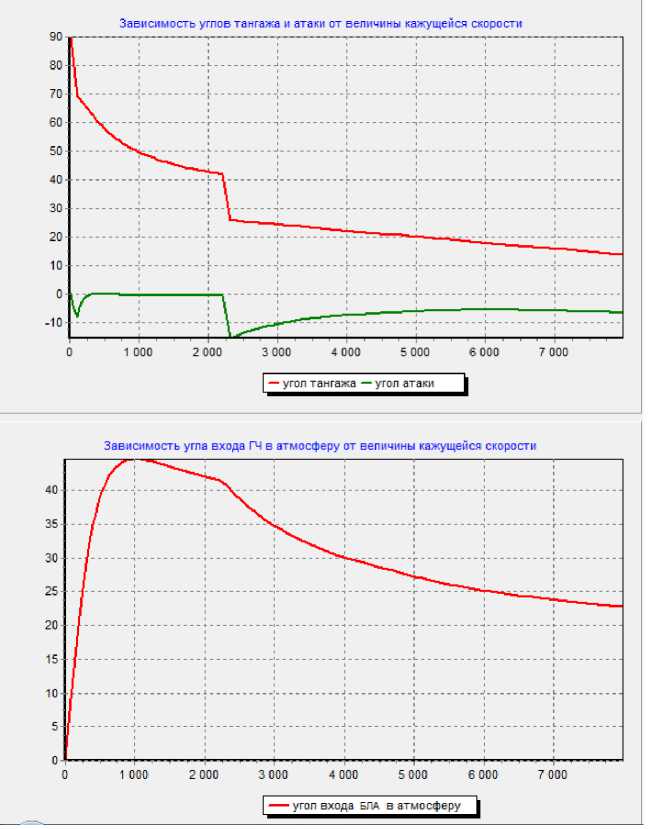
Рис. 2. Изменение угла тангажа и угла входа БЛА в атмосферу

Ниже перечислены более полные результаты моделирования, приведенные в [8].

• 1.    Полученное управление является субоптимальным вследствие использования граничных условий в аналитическом виде. Для повышения точности граничных условий в алгоритм навигации необходимо ввести алгоритм его коррекции, основанный на привлечении более точных моделей гравитационного поля Земли. Таким образом повышается точность выведения.

• 2.    Влияние случайных возмущений компенсируется адаптивными свойствами терминального наведения, а также прогнозированием параметров движения и формирования управления на уменьшающийся каждый раз интервал времени до момента окончания процесса выведения.

• 3.    Полученные оценки при моделировании позволили рационально выбрать дискретность алгоритмов навигации и наведения и тем самым ограничить диапазон требований к бортовым ЭВМ при его реализации.

• 4.    Не вызывает затруднений реализуемость алгоритмов наведения на основе разработанной методики на современных бортовых ЭВМ. Требуемое быстродействие составляет (1-1,5)*10 ⁶ к.о./с.

Обсуждение и заключения. Таким образом, наиболее предпочтительным представляется принцип динамического программирования. Именно его следует использовать при решении задачи синтеза оптимального по расходу топлива управления движением центра масс (задача наведения) БЛА с большой дальностью полета на разгонном участке.

Известное замечание по применимости динамического программирования, так называемое «проклятие размерности», неуместно в задаче формирования управления как функции конечного состояния [5]. Кроме того, использование граничных условий в аналитическом виде существенно упрощает формирование субоптимального управления и позволяет оперативно менять задачи полета. Это существенно расширяет возможность применения названного алгоритма для БЛА различного назначения.

Информатика, вычислительная техника и управление