Способ управления качеством передачи мелких структур изображений в стандарте JPEG2000

В современных методах видеокомпрессии наибольшее применение имеют алгоритмы без адаптации к визуальному восприятию качества разных структур изображения. К таким методам относятся алгоритмы сжатия неподвижных изображений, реализованные в стандартах JPEG и JPEG2000. В системах цифрового телевидения H.264 (H.265), реализованных на основе стандартов MPEG, эти алгоритмы используются для компрессии опорных (I) кадров видеоряда.

Исследователи многих стран предлагают свои адаптивные алгоритмы [1–5] компрессии, основная цель которых заключается в повышении визуального качества изображений. Поиск компромиссных решений между качеством фото - и видеоизображений и степенью их компрессии до сих пор считается актуальной задачей.

В настоящее время существует множество методов анализа и метрик качества изображений. К традиционным метрикам относятся PSNR и MSE, к более сложным – метрики структурного подобия (SSIM) и мультимасштабная MSSIM [6]. Метод SSIM выполняет сравнение двух изображений и оценивает их изменения по яркости, контрасту и структуре [7]. Сравнение пикселей изображений выполняется с помощью окна, в котором оценивается качество изображения, выраженное величиной средней разности (DMOS). Этот метод более популярен, чем PSNR и MSE, т.к. он более информативен и ближе к зрительному восприятию различий между изображениями [7]. В [8] предлагается использовать метрику оценки искажений структур изображения в нормированной системе N-CIELAB, что, по мнению автора, позволяет приблизить объективные результаты анализа качества к субъективным зрительным оценкам.

В статье предлагается способ управления качеством передачи мелких структур изображений в стандарте JPEG2000 на основе автоматической регулировки параметров квантования коэффициентов дискретного вейвлет-преобразования (ДВП), позволяющий повысить эффективность сжатия с допустимыми (минимальными) визуальными искажениями по разработанным критериям в нормированной системе N-CIELAB.

1.    Особенности алгоритма JPEG2000

Рассмотрим особенности алгоритма сжатия изображений в стандарте JPEG2000. В кодере выполняются следующие основные процедуры: а) преобразование цифровых RGB- сигналов исходного файла изображения в сигналы YVU ; б) выполнение вейвлет-преоб-разования для каждой из YVU -компонент изображения; в) квантование коэффициентов ДВП и обнуление малозначащих коэффициентов; г) кодирование битовых плоскостей и арифметическое сжатие.

Преобразование сигналов основных цветов в цифровые сигналы яркости (Y) и цветности (U, V) для вещественного режима выполняется следующим способом [9]:

Y = 0,299 R + 0,587 G + 0,114 B ;

U = - 0,16875 R - 0,33125 G + 0,5 B ;             (1)

V = 0,5 R - 0,41869 G - 0,08131 B .

Дискретное вейвлет-преобразование одномерного сигнала S n длиной N можно выполнить по следующим формулам [9]:

N-1

sLk = ZSj-1,nhn-2k; SHk ZSj-1,ngn-2k,(2)

n=0

где n – номера отсчётов исходного дискретного сигнала; k – номера коэффициентов ДВП преобразованного сигнала в диапазоне от 0 до ( N – 1) / 2; j – номер итерации, изменяющийся от 1 до заданного значения J ; h n – низкочастотные коэффициенты и g n – высокочастотные коэффициенты импульсной характеристики симметричного биортогонального фильтра. В стандарте JPEG2000 рекомендовано [10] использование симметричного биортогонального фильтра Ко-эна–Добеши–Фово (CDF 9/7).

Из преобразования (2) следует, что коэффициенты ДВП S^L представляют собой низкочастотные составляющие, а S^H – высокочастотные составляющие исходного дискретного сигнала. При этом за счёт сдвига импульсной характеристики на 2 k в результате преобразования получаем две составляющие длиной N / 2. Таким образом, в результате первой итерации ( j = 1) имеем масштабированную (уменьшенную) в два раза копию ( S^L ) исходного сигнала и его дополнение ( S ^H ) в виде высокочастотной составляющей. На следующей итерации ( j = 2) процесс повторяется, где исходным сигналом будет низкочастотная составляющая, полученная после первой итерации. После выполнения всех итераций получим масштабированную (уменьшенную) копию исходного сигнала в 2 ^J раза и J дополнительных высокочастотных составляющих.

Обратное преобразование и восстановление исходного сигнала выполняется итерационно по следующей формуле:

( N /2 j ) - 1                ( N /2 j ) - 1

S j - 1,n = Z S L,k h n + 2 k + Z S Hk g + 2 k ,          (3)

k = 0                     k = 0

где j изменяется от максимального значения ( J ) до единицы.

Для двумерного сигнала изображения вейвлет-преобразование выполняется следующим образом. На первой итерации преобразование (2) выполняется последовательно по строкам и столбцам, после чего формируются четыре матрицы (LL, LH, HL, HH) коэффициентов ДВП с размерами, в два раза меньшими ширины и высоты изображения. Принятые обозначения матриц следующие: LL – низкочастотная фильтрация по строкам и столбцам; LH – низкочастотная

фильтрация по строкам и высокочастотная по столбцам; HL – высокочастотная фильтрация по строкам и низкочастотная по столбцам; HH – высокочастотная фильтрация по строкам и столбцам. На второй итерации выполняется аналогичное преобразование для LL матрицы и т.д. Обычно достаточно 4–6 итераций. Такой процесс преобразований эквивалентен операции фильтрации сигналов изображения по частотным субдиапазонам для каждой итерации j .

После выполнения преобразования коэффициенты ДВП квантуются и преобразуются в целочисленные значения, где для каждого субдиапазона итерации j выбирается свой постоянный коэффициент Δ (шаг квантования), на который делятся все элементы матрицы.

Процесс квантования коэффициентов ДВП для каждой итерации ( j ) можно описать следующими формулами:

^^

S j^HH

A *H^H

.^^

S LH =

S_j LH

^^

_;    S HIl =

A LH ’    j

S H _j L

A H^L J’

где S j – исходное значение коэффициента; S_j – квантованное значение. Операция L ... J означает округление вниз до ближайшего целого. Исключение состав-

ляет отрезок «мёртвой зоны» около нуля, в которой квантованные вещественные коэффициенты обнуля-

ются с помощью условия:

if | S / A|< 1; S = 0; else S = S .

Отметим, что для самого низкочастотного субдиапазона шаг квантования выбирается равным единице ( A JL = 1). Значения коэффициентов A ^ HH , A ^LL^H и A ‘HL образуют шкалу квантования. Коэффициенты квантования рекомендованы стандартом и имеют более высокие значения для матриц HH, что обусловлено спадом пространственно-частотной характеристики зрения в области верхних частот.

В стандарте [10] рекомендовано оптимальное соотношение параметров квантования для разных субдиапазонов:

Ab- = , (5)

A o V Y b

где у _b оценивается среднеквадратичной величиной искажения, которое вносится в изображение при единичном искажении коэффициента из субдиапазона b . Эта величина может быть определена на основании анализа вейвлет-преобразования «CDF 9/7». Из таблицы значений соотношения шагов квантования (5), представленной в работе [11], следует, что соотношение шагов квантования для соседних субдиапазонов приблизительно равно двум. В табл. 1 в качестве примера приведена шкала квантования для пяти итераций при заданном шаге для высокочастотного диапазона: A 1 HH = 32.

Табл. 1. Шкала квантования коэффициентов ДВП

j	A *HH	A LLH	A *HL
1	32	16	16
2	16	8	8
3	8	4	4
4	4	2	2
5	2	1	1

Процесс квантования и обнуления коэффициентов ДВП позволяет эффективно сжимать изображения с помощью алгоритма арифметического сжатия или на основе других алгоритмов. В то же время этот процесс вносит основные потери качества в декодированное изображение. Изменение коэффициентов квантования с помощью параметра качества Q позволяет регулировать качество изображения и, следовательно, скорость цифрового потока сжатых визуальных данных.

На последнем этапе выполняется арифметическое сжатие [9] квантованных коэффициентов ДВП. С этой целью матрица коэффициентов разбивается на одинаковые блоки (тайлы), по умолчанию размером 64 × 64. Далее каждый блок кодируется независимо от других. В процессе кодирования коэффициенты в блоке представляются в виде битовых плоскостей. Одну из таких плоскостей составляют знаки коэффициентов. Остальные плоскости соответствуют различным разрядам величин коэффициентов (положение бита в плоскости соответствует положению коэффициента в блоке). При этом сначала кодируется плоскость, соответствующая старшему разряду коэффициентов, затем следующая по убыванию, и т.д. Кодирование одной битовой плоскости одного блока осуществляется в три этапа: кодирование старших бит; уточняющий проход; очищающий проход. Для каждого прохода используется бинарное адаптивное арифметическое кодирование и контекстное моделирование.

При разработке адаптивного алгоритма квантования исследователи обычно предлагают свою шкалу коэффициентов квантования, которая, по их мнению, должна повысить качество изображения. В некоторых работах предлагается использовать разные материнские вейвлеты в зависимости от номера субдиапазона [1,4]. Анализ современного состояния исследований в данной области показывает, что авторы обычно оценивают качество изображения для разных параметров квантователя с помощью интегральных метрик, таких как PSNR, MSE, SSIM и др. [12]. К недостатку таких оценок относится то, что эти метрики не учитывают изменений зрительного восприятия цветовых различий и, следовательно, искажений отдельных участков изображения в зависимости от их цвета, контраста и детальности.

2.    Оценка искажений в системе N-CIELAB

Идея предлагаемого способа настройки параметров квантования заключается в использовании объек- тивных критериев оценки искажений мелких структур изображения, которые отличаются по признакам их детальности и по степени заметности искажений цветового контраста выделенных объектов. В качестве критериев предложено использовать числовые меры искажений мелких структур декодированного изображения в нормированной колометрической системе N-CIELAB [8], по которым выполняется анализ искажений (разрушений) их структурных признаков.

Описание системы N-CIELAB

Колометрическая система CIELAB относится к классу равноконтрастных систем [13] и широко используется для оценки цветовых различий и точности цветопередачи крупных деталей изображения. С уменьшением размеров деталей свойство равнокон-трастности CIELAB теряется, т.к. в системе не учитывается спад контрастной чувствительности зрения. Суть нормировки и переход в систему N-CIELAB заключается во введении в формулу оценки цветовых различий (контраста) между двумя деталями изображения (1 и 2) весовых коэффициентов по координатам светлоты L ^* и цветности a ^* , b ^* :

/ T* T* \ \ / 7 * 7 * V । L - L2 1 । a - a 2 1 1 b - b2 1 I T* I "I" I I I 7 * I V L5 J ( a 5 J ( bs J где ( L*1a*1b*1) – цветовые координаты первой детали и (C2a*2b2) - цветовые координаты второй детали; L*5, a*5 и b5 - весовые коэффициенты по светлоте и цветности, заданные количеством минимальных цветовых порогов MPCD в зависимости от размера (5) детали.

Цветовые координаты L^*a^*b^* для каждого пикселя изображения получены с помощью преобразования основных цветов (RGB) в цветовое пространство (XYZ), а затем с помощью формул [13]:

L* = 116 f ( Y / Y o ) - 16;

a * = 500 [ f ( X / X o ) - f ( Y / Y o ) ] ; (7) b * = 200 [ f ( Y / Y o ) + f ( Z / Z o ) ] ;

где

[ t ^1/3, if t >  0,008856, f ( t ) =                  ,          ,

[7,7871 + 0,13793, if t < 0,008856, и значения Xo, Yo и Zo являются координатами эталонного белого цвета.

Весовые коэффициенты получены экспериментальным путём раздельно для трёх цветовых координат L^* , a^* и b^* в зависимости от размера одиночной детали в 1, 2, 3, 4 и более пикселей, расположенных на равномерном фоне. В частности, для самых мелких деталей эти значения равны: L 1 « 6 , a * « 40 и b 1 » 55 [14].

Использование весовых коэффициентов позволяет оценивать цветовой контраст деталей в системе

N-CIELAB в зависимости от их размера с учётом контрастной чувствительности зрения. Экспериментально доказано, что при пороговом значении цветового контраста K ≈ 1 мелкие детали начинают различаться глазом, и этот порог мало зависит от цвета детали и яркости окружающего фона.

Способ оценки искажений можно разделить на два этапа. На первом этапе выполняется алгоритм идентификации мелких структур оригинального изображения, который основан на результатах анализа структуры микроблоков с размером 3×3 пикселя. Для такого микроблока имеем шесть цветовых переходов по горизонтали и шесть цветовых переходов по вертикали, т.е. всего 12 переходов.

Мелкие структуры в микроблоке можно разделить на следующие типы: точечные объекты, фрагменты тонких линий, фрагменты контуров, фрагменты текстур. Максимальное количество цветовых переходов ( n ) между соседними пикселями внутри микроблока будет равно n = 12 (фрагмент текстуры). Минимальное количество цветовых переходов равно n =2.

Идентификация микроблока выполняется по следующему алгоритму. В каждом микроблоке m вычисляются двенадцать значений контраста между соседними пикселями:

K m , p

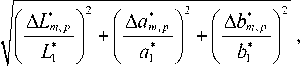
где значения A L * _m , p , A a* _m ,p и A b * p определяют контраст между соседними пикселями по светлоте и по цветности для цветового перехода с номером p . На каждом шаге вычислений (8) проверяем условие

K m , p >  ¹ ,

при выполнении которого принимаем решение о том, что изменение контраста между соседними пикселями заметно глазом, и увеличиваем значение счетчика ( n ) обнаруженных цветовых переходов на единицу. После анализа всех цветовых переходов в микроблоке выполняем его идентификацию по следующему критерию.

Если количество переходов с цветовым контрастом (9) превышает значение n = 1, то в микроблоке присутствует мелкая структура, различимая глазом. Если данное условие не выполняется, то мелкая структура не различается глазом.

После анализа всего изображения получим выделенные участки изображения с различимыми мелкими структурами в виде микроблоков с размерами 3 × 3 пикселя. Количество таких микроблоков обозначим N m . Остальные участки классифицируем как микроблоки с равномерными изменениями цветовых координат и обозначаем их количество символом N F . По значению N m можно определить уровень детальности ( FDL ) изображения, который показывает процент участков изображения с мелкими структурами

FDL =--- N m ---100%.                   (10)

( N m + N_f )

На втором этапе оцениваются искажения компрессированного изображения. Для оценки искажений в выделенных участках с мелкими структурами предлагается следующая методика [8]. В каждом идентифицированном микроблоке m вычисляем 12 отклонений контраста между цветовыми переходами оригинального Km,p и искажённого Km,p изображений dEm,p = |Km,p - Km,p|                                (11)

и находим максимальное отклонение dEm = max(dEm,p).

Далее проверяем условие dEm > 0,5.                                      (12)

Если условие (12) выполняется [8], то принимается решение о том, что отклонения цветового контраста в микроблоке m заметны глазом и такой блок идентифицируется как искажённый in .

После анализа всех микроблоков получим объективную оценку искажений в виде отношения:

8 = N m 100%,                             (13)

m где значение N,m определяет количество искажённых микроблоков.

После вычислений значения 8 выполняем анализ качества компрессированного изображения по следующему критерию:

8< 1%.                                     (14)

В результате экспериментальных исследований (см. раздел 4) доказано, что при выполнении этого условия искажения мелких структур практически незаметны для глаза.

Дополнительно можно использовать среднюю оценку искажений по всем микроблокам с мелкими структурами:

Nm dEn =   Е dEm ,                         (15)

^N m m = 1

которая соответствует метрике MFSD ( Metric of Fine Structures Distortion ) [8].

Таким образом, на основе метрики MFSD мы предлагаем новый критерий (14) оценки качества изображений.

3.    Алгоритм адаптивного квантования

В качестве основы шкалы квантования выбрано оптимальное соотношение параметров квантования для субдиапазонов в соответствии с критерием (5) и табл. 1.

Регулировка качества передачи изображения заключается в автоматической настройке параметра квантования A HH на допустимые искажения в соответствии с критерием (14). По умолчанию выбрано начальное значение A HH = 32. В процессе настройки этот параметр изменяется дискретно на заданный шаг регулировки ±о , пока не будет выполнено условие (14).

Таким образом, мы используем классическую систему автоматического регулирования по заданному критерию.

Основная задача исследований – это выбор оптимального значения шага о с целью минимизации вычислительных затрат при условии обеспечения заданного качества изображений.

Для решения этой задачи реализован программный модуль в среде С++, выполняющий следующие функции:

• 1.    Открытие тестового изображения и линейное преобразование цифровых сигналов оригинального изображения из RGB- в YUV- формат.

• 2.    Преобразование цифровых сигналов оригинального изображения из RGB- в L^*a^*b^*- формат.

• 3.    Идентификация микроблоков (3 × 3) оригинального изображения с мелкими структурами.

• 4.    Выполнение прямого ДВП для составляющей яркости (Y) и для составляющих цветности (U и V) с заданным количеством итераций J = 5 .

• 5.    Квантование коэффициентов ДВП, где на первом шаге использованы параметры квантования по умолчанию (табл. 1).

• 6.    Выполнение обратного квантования и обратного ДВП с преобразованием цифровых сигналов изображения из YUV- в L^*a^*b^*- формат.

• 7.    Вычисление параметра искажений е .

• 8.    Проверка качества декодированного изображения и настройка оптимального параметра A HH :

• а)    При выполнении критерия (14) увеличиваем A^HH на шаг о и выполняем п. 5-7 до тех пор, пока е не станет больше 1 %. Фиксируем оптимальное значение AHH = AHH - о;

• б)    При невыполнении (14) уменьшаем A^HH на шаг о и выполняем п. 5 - 7 до тех пор, пока е не станет меньше 1%. Фиксируем оптимальное значение AHH = AHH - о.

• 9.    Сжатие квантованных коэффициентов ДВП на основе модифицированного алгоритма кодирования длин серий нулей [15] с переменной длиной кода. Таким образом, после выполнения алгоритма мы получим оптимальное значение A₁^HH для анализируемого изображения, при котором будет обеспечиваться его высокое качество. Это значение можно передать в заголовке файла или кадра видеоданных с целью обратного квантования и декодирования.

4.    Результаты экспериментов

К особенностям реализации разработанного алгоритма относится следующее: в качестве материнского вейвлета выбран CDF 9/7; ширина «мёртвой» зоны квантования равна нулю; для каждого квантованного коэффициента ДВП (4) использовано 12 бит, включая один знаковый разряд.

Алгоритм сжатия в отличие от стандартного алгоритма [9] выполнен по упрощённой схеме. Размер тайла соответствует размеру изображения. В процессе сжатия последовательно по субдиапазонам каждый коэффициент ДВП проверяется на выполнение условия S j = 0 . Если это условие выполняется, вычисляется длина серии нулей. Если не выполняется, то кодируется ненулевой коэффициент. Серии нулей и ненулевые коэффициенты кодируются кодами переменной длины в соответствии с кодовой таблицей. В таблице [15] содержатся 4 префикса длин кода серий и 5 префиксов ненулевых коэффициентов. Каждый префикс соответствует заданной разрядности длины кодов и определяет их динамический диапазон. Отметим, что параметры таблицы выбраны на основе анализа статистики коэффициентов ДВП фотореалистичных изображений.

В результате экспериментов получено, что эффективность сжатия нашего алгоритма практически не уступает стандартному алгоритму сжатия JPEG2000, реализованному в приложении Adobe Photoshop CS6.

Для получения оптимального значения о был выполнен анализ качества оригинальных фотореалистичных изображений из базы данных [16] лаборатории LIVE, а также из других баз данных.

На рис. 1 показаны примеры тестовых изображений: «Женщина в шляпе» (Woman_hat), «Байкеры» (Bikes) и «Попугаи» (Parrots). В табл. 2 приведены результаты их анализа.

Рис. 1. Примеры тестовых изображений из базы данных лаборатории LIVE

Для каждого изображения приведён уровень детальности ( FDL ), который показывает процент участков изображения с мелкими структурами. Серым цветом выделен оптимальный параметр A HH , при котором выполняется критерий (14). Для сравнения приведена оценка искажений по метрике SSIM.

Табл. 2. Зависимости искажений тестовых изображений от параметров квантователя

Женщина в шляпе (FDL = 21 %)
Δ 1 HH	ε, %	d E N	k сж	SSIM
20	0,0	0,147	5,9	0,989
24	0,0	0,172	6,6	0,987
28	0,1	0,197	7,3	0,984
32	0,3	0,222	8,0	0,982
36	1,3	0,248	8,7	0,979
40	3,3	0,272	9,3	0,977
44	6,1	0,296	10,0	0,975
Байкеры (FDL = 56 %)
Δ 1 HH	ε, %	d E N	k сж	SSIM
20	0,0	0,173	4,2	0,995
24	0,0	0,201	4,6	0,994
28	0,2	0,231	5,0	0,993
32	1,2	0,261	5,3	0,992
36	3,8	0,290	5,7	0,990
40	7,9	0,319	6,0	0,989
44	13,8	0,348	6,3	0,988
Попугаи (FDL=9 %)
Δ 1 HH	ε, %	d E N	k сж	SSIM
20	0,0	0,153	8,2	0,987
24	0,0	0,180	9,4	0,985
28	0,0	0,203	10,7	0,983
32	0,3	0,225	12,0	0,981
36	1,2	0,250	13,3	0,979
40	3,2	0,274	14,7	0,977
44	6,8	0,299	16,1	0,976

В результате анализа более ста оригинальных изображений из разных баз данных получены следующие результаты.

• 1.    Для большинства тестируемых изображений с уровнем детальности FDL<50% высокое качество обеспечивается при значении параметра Δ₁^HH ≤32 . При этом средняя оценка искажений (15) не превышает значения 0,25.

• 2.    Для настройки оптимального значения Δ₁^HH оптимальным шагом регулировки будет значение σ = ± 4. В этом случае достаточно выполнить одну итерацию изменения параметра Δ₁^HH .

• 3.    Оценка искажений по метрике SSIM не дает однозначного решения. В частности, если для обеспечения высокого качества выбрать условие SSIM>0,98, то для изображений с высокой детальностью и контрастностью (пример «Байкеры») значение Δ1^HH может превышать начальное значение Δ₁^HH почти в два раза.

5.    Оценка быстродействия алгоритма

Отметим, что при настройке параметров квантования на оптимальные значения качество остальных участков изображения ( N F ) соответствует высокой оценке по критерию незаметности цветовых различий:

NF dEF=1 ∑dEk<2,3, (16) NF k=1

оценивает среднее отклонение цветовых координат оригинального и искажённого изображения в системе CIELAB внутри микроблока ( k ), в котором отсутствуют различимые глазом мелкие структуры; – номер пикселей в микроблоке (3 × 3). Выражение (16) даёт среднюю оценку по всем «фоновым» микроблокам N F .

При реализации адаптивного алгоритма сжатия в мультимедийных приложениях необходимо оценить его быстродействие. Время выполнения алгоритма можно оценить количеством вычислительных операций (КВО), которое требуется для выполнения п. 1–8. К таким операциям относятся математические операции сложения, вычитания, умножения, деления, возведения в степень, а также логические операции.

Наша задача – это оценка дополнительных вычислительных затрат, которые потребуются для адаптивной настройки квантователя. Поэтому ниже приводятся результаты поэтапных вычислений КВО.

Введём следующие обозначения операций: (+) сложение или вычитание, (×) умножение, (/) деление, (^) возведение в степень, (!=) проверка условия завершения цикла, (>) проверка логических условий.

На первом этапе оценим приблизительное значение КВО, необходимое для кодирования изображения (п. 1 и п. 4–5) без учёта алгоритмов адаптивной настройки квантователя и сжатия.

Пункт 1: преобразование RGB в YUV. Из форму -лы (1) следует, что для преобразования одного пикселя изображения потребуется 16 операций:

КВО 1 =[9(×) + 6(+) +1(!=)] =16.

Пункт 4: прямое ДВП. На первой итерации с учётом использования вейвлета CDF 9/7 получим, что для одного коэффициента ДВП для каждой составляющей по яркости и по цветности потребуется 68 операций:

2[9(×) +9(+) +1(!=) +7(×) +7(+) +1(!=)].

Здесь согласно формуле (2) учитывались 9 операций умножения и 9 сложения для НЧ составляющей и 14 операций для ВЧ составляющей при выполнении преобразования по строкам и то же количество при выполнении преобразования по столбцам. Также для каждого вычисления учтена операция проверки условия завершения цикла. Для всего изображения получим 68⋅Im операций, где Im – это размер изображения в пикселях. На второй итерации 68(Im /4), на третьей 68(Im /8) и т.д. В итоге, для пяти итераций для вычисления одного коэффициента ДВП по каждой состав- ляющей имеем КВО = 100. Для всех тех составляющих получим КВО4 = 300.

Пункт 5: квантование коэффициентов ДВП. Из формулы (4) следует, что для одного коэффициента ДВП потребуется всего 3 операции: 2(/) + 1(!=). В этом пункте мы учитываем, что операции деления и округления оцениваются числом 2. Суммарное количество операций будет равно КВО 5 =9.

В итоге получим, что для выполнения кодирования потребуется 325 операций (КВО 1,4,5 ) на один пиксель исходного изображения. Так как алгоритм симметричен, то на обратное декодирование и преобразование потребуется то же значение КВО.

При использовании адаптивного квантования для одного шага настройки необходимо выполнить пункты 2–3 и 5–8. Для этого потребуется следующее количество операций.

Пункт 2: преобразование цифровых сигналов оригинального изображения из RGB - в L^*a^*b^*- формат. Для линейного преобразования RGB в XYZ потребуется аналогично (1) 16 операций. На выполнение преобразования (7) получим

5[(/) +(>) +(^)] +3[(+) +(×)] + 1(!=)

операций. В итоге имеем КВО 2 =38.

Пункт 3: идентификация микроблоков (3×3) оригинального изображения с мелкими структурами. Для расчётов использованы формулы (8) и (9), на основании которых получено, что вычисление контраста для каждого цветового перехода потребует 10 операций: 3(/) +2(+) +4(^) + 1(>). Для двенадцати переходов, с учётом проверки окончания цикла, получим 121 операцию, что в пересчёте на один пиксель даёт значение КВО 3 ≈ 13.

Пункт 6: выполнение обратного квантования и обратного ДВП с преобразованием цифровых сигналов изображения из YUV- в L^*a^*b^*- формат. В результате получим КВО 6 ≈ КВО 5 + КВО 4 + КВО 2 =347.

Пункт 7: вычисление параметра искажений ε . Из формул (11) и (12) с учётом (8) следует, что для анализа каждого идентифицированного микроблока (3 × 3) потребуется 158 операций, что в пересчёте на один пиксель даёт значение 18. Так как количество микроблоков определяется уровнем FDL , то общее количество операций можно оценить, как КВО 7 ≈ 18( FDL /100).

Пункт 8: настройка квантователя. Для выполнения этого пункта потребуется следующее количество операций

КВО8= LΔ [КВО5+ КВО6+ КВО7], где LΔ – количество шагов настройки. Для численной оценки выберем параметр FDL =50, что даёт КВО8=365 LΔ.

В итоге, общее количество операций на один пиксель изображения, необходимое для выполнения адаптивного алгоритма, равно:

КВО 1 – 8 ≈ 325+407+365 L Δ , где первое слагаемое определяет количество операций без адаптивной настройки квантователя. Для одного шага настройки L Δ = 1 получим КВО 1 –8 ≈ 1097, что примерно в 3 раза превышает КВО неадаптивного алгоритма.

Отметим, что расчёты выполнены без учёта оптимизации алгоритма [17] и кода программы с целью минимизации вычислительных затрат.

Реальное время выполнения алгоритма зависит от многих факторов, в первую очередь, от архитектуры и производительности микропроцессорной системы.

В качестве примера выполним расчёт КВО, необходимое для кодирования изображения в ТВ -формате с количеством пикселей

Im =720×576=414720 и L Δ =1.

В результате получим: КВО 1–8 ≈ 455 ∙10⁶. Используем процессор Intel Core 2 Quad Q6600 [18] с пиковой производительностью 38,4 Гигафлопс. Время выполнения адаптивного алгоритма будет равно t ≈ 12 мс.

Таким образом, использование адаптивной настройки увеличивает время выполнения алгоритма кодирования примерно в три раза. При этом быстродействие алгоритма декодирования не изменяется.

Заключение

В заключение отметим отличительные особенности предложенного способа управления качеством передачи мелких структур изображений.

Анализ качества изображений и настройка квантователя выполняются не по интегральным оценкам (SSIM, PSNR и др.), а по критерию (14), определяющему допустимые визуальные искажения выделенных участков с мелкими структурами в системе N-CIELAB. При этом искажения оцениваются относительным количеством микроблоков (3 × 3), в которых максимальное отклонение контраста превышает зрительный порог.

С помощью разработанной программной модели кодера JPEG2000 экспериментально определён начальный параметр квантования Δ 1 ^HH =32 и оптимальный шаг регулировки s = ± 4, при которых выполняется адаптивное квантование и настройка изображения на высокое качество передачи мелких структур с минимальными вычислительными затратами алгоритма кодирования.

К перспективным исследованиям относится внедрение и анализ эффективности разработанного алгоритма в мультимедийных системах передачи видеоданных на основе стандартов MPEG-2 и MPEG-4.