Способ вычисления площади листа груши по линейным измерениям с помощью расчетных коэффициентов и методов вариационной статистики

Изучение морфологических признаков растения, их изменчивости и сортовой устойчивости позволяет получить подробные сведения о генотипе в целом и его взаимодействии со средой. Взаимосвязь продуктивности с устойчивостью сорта к основным стрессорам несомненна, однако на нее влияют и другие факторы, в первую очередь активность и характер работы ассимиляционного аппарата.

Лист — орган высшего растения, функционально предназначенный для фотосинтеза, транспирации и газообмена. Обеспечивая растение пластическими веществами и участвуя в непрерывном транспорте веществ по проводящим структурам, он играет полифункциональную роль в поддержке жизнедеятельности, развитии и адаптации растительного организма.

Среди других вегетативных органов растения именно лист представляет собой структуру, наиболее активную в метаболическом отношении и разнообразную морфологически (1-3). Морфологическое исследование листового аппарата плодовых культур проводится главным образом в связи с изучением фотосинтетической активности, при этом используется один из метрических индексов — площадь листовой пластинки (4). Современные компьютерные технологии и статистические методы позволяют повысить точность анализа и выявить закономерности, которые не удавалось обнаружить ранее из-за серьезных погрешностей.

В настоящее время накоплен опыт по применению методов, которые с разной степенью точности позволяют определить площадь листьев: весовой, планиметрический, метод эталонов, определение площади по удельной массе высечек листа, метод электрографического порошка. Подобные разработки имеют несколько существенных недостатков. Они либо трудоемки и малопроизводительны, либо их использование связано с отделением листьев от растения и невозможностью дальнейшего наблюдения за ними. Поэтому все большее внимание уделяется математическому методу расчета площади листа по линейным размерам. Описано несколько способов измерения площади листьев. Их общее достоинство заключается в выведении на основе регрессии математически обоснованных формул площади листьев для различных видов и сортов сельскохозяйственных культур в процессе массовых определений (5-8). Н.Ф. Коняев применял метод линейной регрессии, позволяющий вывести формулы площади листьев для различных овощных культур (9). Недостаток этого метода состоит в том, что при равноценности формул, выведенных по длине и ширине или одной длине листа, индивидуальные отклонения площади больше в вариантах, где формула выведена по длине листа, и меньше в тех случаях, когда она выведена по длине и ширине. Для повышения точности целесообразно выводить формулы для каждого сорта отдельно. В.Я. Волков и В.Ф. Селевцев предложили серию из трех математических моделей определения площади листьев огурца по их длине и ширине на разных стадиях роста (10). Длина листа в этом случае — это длина линии сегмента (части) рисунка листовой пластинки от кончика до точки, перпендикулярной пересечению с линией рисунка по ширине пластинки, ближе к черешку листа. Метод применим исключительно к определенной форме листовой пластинки с учетом ростовых особенностей. N.S. Robbins и D.M. Pharr использовали метод множественной регрессии с учетом особенностей роста и условий выращивания (11). Длина листа огурца измерялась от кончика до конечной точки центральной жилки. Однако в этом случае требуется выводить индивидуальную формулу для каждого сорта не только исходя из особенностей генотипа, но и в зависимости от условий выращивания. Разработан метод определения площади листа земляники с помощью специальной шкалы, построенной на основании методов вариационной статистики (12). Его достоинство состоит в выявлении связи между площадью листа, определенной планиметром, и его параметрами. Эта связь выражается уравнением и используется для расчета площади листа земляники по центральной жилке, а также получения шкалы для практического использования. Недостаток метода заключается в том, что для расчетов ошибки определения не более 5 % необходимо вычислять площадь листьев в пределах от 15 до 220 см2.

В настоящей работе мы впервые для культуры груши применили два метода оценки площади листовой поверхности: на основании пере-счетного коэффициента и посредством уравнений регрессии, связываю-212

щих площадь листа с его линейными размерами (длиной и шириной).

Цель работы — определение поправочного коэффициента и получение регрессионной модели для вычисления площади листа без отделения от растения у различных сортов груши с минимальной погрешностью.

Методика. Исследования проводили на коллекционном участке (посадки 1998 года) Всероссийского НИИ цветоводства и субтропических культур в 2001-2004 годах. Биометрические параметры листа изучали на 10 сортах груши разных сроков созревания: Pirus communis L. — Бере Жиффар, Вега (ранне-летние); Вильямс, Черноморская Янтарная (летние); Бере Боск, Рассвет, гибрид ¹ 8520, Нарт; Pirus serotina Rehd. — Кильчу, Чоо-чен-сок (осенне-зимние). Листья отбирали из средней части кроны для каждого сорта по 10 шт. в 3 повторностях (14). У каждого листа измеряли длину вдоль центральной жилки и ширину в наиболее широком месте с помощью линейки, площадь листьев определяли методом планиметрирования с использованием палеток (пленочных пластинок размером 15½10 см с нанесенными квадратиками площадью 0,5 см²).

Данные по длине и ширине листовой пластинки применяли для определения переводного коэффициента и вычисления площади на основании методов вариационной статистики (15-22). Связь между фактической площадью листа, и его параметрами выражали с помощью уравнения, которое использовали для теоретического расчета площади листа груши. При построении регрессионной модели в качестве независимых переменных использовали параметры: длина (L), квадрат длины (L2), ширина (W), квадрат ширины (W2) и произведение длины и ширины (LW).

Обработку данных выполняли методами кореляционного и регрессионного анализов, описательной статистики с использованием пакета программ Statistica for Windows 5.5 (23) и Microsoft Excel 7.0.

Результаты. В основе метода определения площади листа с помощью расчетного коэффициента лежит соответствие между формой листа (как показателем особенности генотипа) и геометрической фигурой, ее описывающей (эллиптическая, узко- или обратно-яйцевидная, овальная, округлая, ланцетовидная) (24, 25). Многообразие форм листовых пластинок предполагает широкое варьирование выбора линейных размеров. В большинстве случаев используются два показателя — длина и ширина, которые имеют высокую корреляцию (0,98) с площадью листовой поверхности (26). Определив вид фигуры, в которую вписывается лист, можно рассчитать коэффициент между его фактической площадью, измеренной прямым методом (планиметрическим), и площадью фигуры (27-29).

Коэффициент определяется как отношение фактической площади к площади прямоугольника со сторонами x и y:

К = S/L½W, [1] где К — коэффициент (безразмерная величина), L — длина листа (см), W — ширина листа (см), S — площадь листа (см²), определенная прямым методом.

Чтобы упростить вычисление коэффициента, можно рассчитать его по длине или ширине:

К = S/L2, [2]

К = S/W2. [3]

Метод расчетного коэффициента не требует сложной вычислительной техники, им легко пользоваться в полевых условиях. При этом можно вести длительные наблюдения, например определять изменение площади листа в процессе развития растения от начальных стадий до отмирания.

По формулам [1, 2, 3] мы определяли три варианта расчетного ко- эффициента — К1, К2, К3. Для каждого из них были получены три выборки по 100 значений, которые подвергали статистической обработке с вычислением среднего значения (X) и коэффициента вариации (Cv, %), который изменялся от 1,18 (для K1) до 2,57 (для K2). Чем меньше был коэффициент вариации, тем меньше оказывались отклонения каждого значения выборки от вычисленного среднего значения. Анализ показал незначительную разницу (0,11-0,65 %) при применении формул с расчетным коэффициентом для различных сортов. При вычислении по одной формуле на 10 сортах груши минимальная погрешность составила 0,1 %. Наиболее точным способом определения площади листьев груши с помощью расчетных коэффициентов служит расчет по произведению длины и ширины листа с использованием следующей формулы: S = 0,69 ½ (LW). Эту формулу можно применять для быстрого вычисления площади листьев груши и других плодовых культур с аналогичной формой листовой пластинки. Предложенный метод позволяет наблюдать за изменением площади листьев на протяжении длительного времени и определять скорость фотосинтеза (количество накопленных листьями органических веществ за определенный промежуток времени).

Поиск оптимальной математической модели методами вариационной статистики для теоретического определения площади листа был проведен методами линейного и множественного регрессионного анализа. Тесты показали, что для разных сортов груши включение в регрессионную модель ширины обеспечило более точный подсчет площади листа (R2 = 0,98). Подобный способ оценки площади листа необходим для изучения связи между площадью листовой пластинки и ростом растения. Площадь одного листа или листьев одного растения, вычисленная по формулам, может точно совпадать или незначительно либо существенно отклоняться от показателей, полученных с помощью планиметра. Объясняется это индивидуальными различиями растений и возрастными изменениями формы листа. Чем ближе расположены точки к прямой графика регрессии, тем меньше отклонения от истинной площади.

Формулы можно вывести как по измерениям длины и ширины, так и по измерению только длины листа. По равноценности и точности индивидуальные отклонения площади в наших опытах оказались больше при выведении формулы по длине листа и меньше — по длине и ширине. Было целесообразно выводить формулы для каждого сорта отдельно, поскольку взаимная замена формул для разных сортов снижала точность определения площади. Если при вычислении площади листа по одной формуле для нескольких сортов наблюдалась минимальная погрешность, то эту формулу можно было считать общей для культуры груши. При анализе полученных данных была установлена тесная положительная связь между параметрами длины, ширины и площади листовой пластинки, что позволило рассчитать уравнения линейной и криволинейной (параболической) регрессии площади листа груши.

Модель отбора нуждалась в балансе между точностью вычисления и числом изменчивости (наименьшее число переменных, необходимых для вычисления). Оценив коэффициент детерминации (R²), F -критерий Фишера, средний квадрат ошибки (mS) для каждого расчета регрессии, мы выявили несколько уравнений, пригодных для вычисления площади листа груши (табл.). После пошагового подбора наиболее точным оказалось уравнение Y = - 6,613161 - 0,272064 ½ (LW) + 4,9738 ½ W (R² = 97,91) при p < 0,01. Уравнение Y = 0,922581 + 0,660898 ½ (LW) было менее точным (R² = 97,13 %), но поскольку коэффициент корреляции между пло-214

щадью и произведением длины листа на его ширину оказался высок ( r = 98,5), мы использовали эту математическую модель линейной регрессии.

Регрессионные модели, описывающие зависимость площади листа от его длины и ширины у сортов груши

Модель	R2	mS	F
Модель с использованием одной длины:
Y = - 32,7338 + 6,89464 ½ L	87,21	59,4	191,01
Модель с использованием одной ширины:
Y = - 11,565 + 8,37592 ½ W	97,54	66,44	1111,15
Модель с использованием произведения длины и ширины:
Y = 0,922581 + 0,660898 ½ (LW)	97,13	66,16	950,95
Модели с использованием квадратов длины и ширины:
Y = - 4,87168 + 0,426423 ½ L2	87,67	59,72	199,15
Y = 5,65063 + 1,01831 ½ W2	98,13	66,84	1473,21
Модель с использованием одной длины и ее квадрата:
Y = 434,525 - 108,44 ½ L + 7,1152 ½ (L2)	91,16	41,05	139,22
Модели с использованием длины, ширины, их квадратов:
Y = - 6,613161 - 0,272064 ½ (LW) + 4,9738 ½ W	97,91	33,34	632,81
Y = 267,743 + 4,32894 ½ L2 - 68,7042 ½ L + 6,70968 ½ W	99,09	22,15	940,88
Y = 271,486 + 0,773545½ (LW) + 4,01169½L2 - 66,374½L	98,89	22,45	775,85
Y = 553646 ½ W2 + 0,286783 ½ (LW) - 39,9336 ½ W + 21,5484 ½ L - 1,36161 ½ L2	99,99	3148,99	140398,98
Y = 66,3173 - 0,557339 ½ L + 0,286783 ½ (LW) - 28,8807 ½ W + 4,15485 ½ W2	99,17	16,89	752,95

П р и м е ч а н и е. Y — площадь, L — длина, W — ширина; R2 — коэффициент детерминации, mS — средняя сумма квадратов регрессии, F — значение критерия Фишера.

Анализ графиков (рис.) и суммирование полученных данных показали, что регрессионные модели с единственным измерением LW могут служить для точного вычисления площади листа у разных сортов груши.

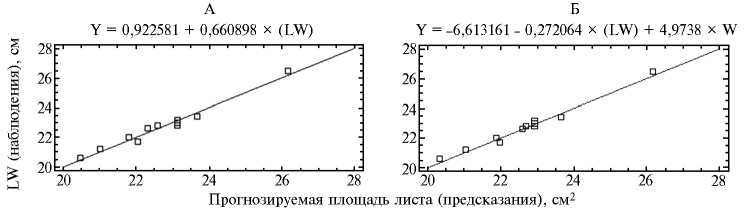
Графики уравнений линейной (А) и множественной (Б) регрессии для моделей вычисления площади листа груши по его длине (L) и ширине (W) .

Значения F -критерия Фишера, полученные при дисперсионном анализе, указывают на то, что отклонение от линейности было обусловлено случайным выборочным варьированием и нулевая гипотеза об отсутствии линейной связи отвергалась. Поскольку Fф > Fst, то между сортами наблюдалась существенная разница на уровне 1,0 %. Все модели были статистически значимыми (p < 0,01), уровень значимости для взаимодействия признаков составил 99,0 %. На основании полученного уравнения регрессии мы разработали программу расчета площади листа в MS Exсel 7.0. Предложенный нами способ расчета площади листьев груши дает возможность построить шкалу, отградуировав ее в единицах площади. Для этого полученное уравнение необходимо решить относительно L и W. Прикладывая к шкале лист груши по его длине c поправкой на ширину, находим площадь листа. Чтобы ускорить и упростить процедуру при проведении 50-100 измерений, можно построить радиальную диаграмму. Дуги по диаграмме проводят через каждый 1 см длины листа. Для определения площади нужно приложить лист центральной жилкой к началу диаграммы (точка 0) и, определив длину, сделать поправку на ширину (или, используя предварительно полученные биометрические данные, считать по диаграмме площадь).

Разработанные методы могут использоваться для определения площади овальных, яйцевидных и нерассеченных листьев у южных плодовых (яблоня, груша, вишня, слива) и субтропических культур (цитрусовые, фейхоа, хурма, чай), древесных, кустарниковых и травянистых растений.

Таким образом, наиболее точным способом определения площади листьев груши служит расчет с единственным измерением «произведение длины и ширины». Тесная положительная связь показателей длины и ширины листовой пластинки дает возможность с помощью методов расчетного коэффициента, регрессионного уравнения, номограммы и радиальной диаграммы точно вычислять площади листа у различных сортов груши с минимальной погрешностью в полевых условиях. Компьютерная технология позволяет ускорить и упростить подобные расчеты.