Способы представления экспериментальных данных при обосновании плотности сети инженерно - геологических исследований техногенных массивов

При исследовании сложных объектов горной промышленности в рамках ограниченных временных и финансовых ресурсов все чаще используются методы построения их моделей. Это позволяет прогнозировать поведение системы во времени и пространстве, что значительно снижает затраты на исследования и последующий мониторинг ее параметров. В качестве объекта моделирования может выступать как отдельная характеристика горнопромышленного комплекса, так и их совокупность, в последнем случае возникает необходимость имитировать изменение каждого параметра системы и их влияние друг на друга [1].

Любой техногенный массив представляет собой сложный, слабо детерминированный и эволюционирующий объект исследования. Формирование и последующее его поведение в значительной мере соответствуют подходу, предложенному школой Ильи Пригожина: в развитии любой системы чередуются периоды, в течение которых ее состояние может быть характеризовано, то как "в основном детерминированное", то как "в основном случайное", когда дальнейшее поведение становится в высокой степени неопределенным. Очевидный пример - сезонность намыва, при этом начало и окончание ведение работ являются моментами, когда поведение массива становится на некоторое время «в значительной степени случайным», так как в это время нарушается установившийся баланс в системе. На рисунке 1. представлен график изменения некоторой условной характеристики наблюдаемого объекта с учетом периодов адаптации (внутренние процессы, протекающие без качественных изменений во внешней среде) и бифуркаций (при этом некоторые компоненты окружающей среды могут находиться в критических (переходных) состояниях) [4, 5].

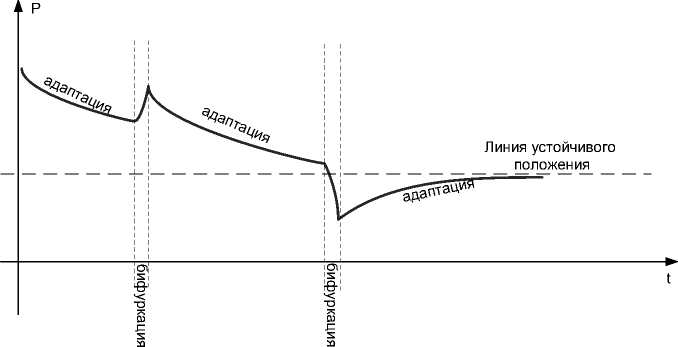
Рис. 1. График изменения параметра при адаптациях и бифуркациях.

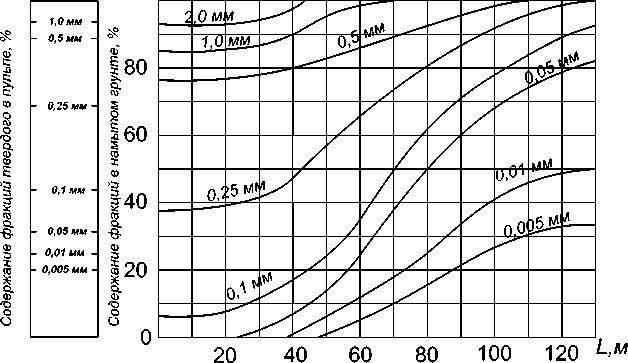
Согласно правилам и рекомендациям проведения инжерно-геологических исследований перед началом непосредственного выполнения работ необходимо установить систему и параметры инженерно-геологического опробования. При этом первоочередной задачей является проектирование сети инженерно-геологических исследований, в качестве ее основополагающих параметров выступает ее структура (способ расположения точек опробования) и плотность (расстояние между точками опробования. Принципиально можно выделить два основных типа структуры сети: геометрически правильная (квадратная, ромбическая и др.) и распределенная (нормирующий плотность сети признак нелинейно связан с пространственными характеристиками массива). Применение первого типа структур необходимо при полном отсутствии данных об исследуемом массиве, когда невозможно выделить каких-либо закономерностей в изменении наблюдаемых параметров объекта. В условиях, когда заранее известно, что характеристики массива имеют функциональную пространственную изменчивость перспективнее использовать сети с распределенной структурой. Намывной массив, сформированный относительно однородными техногенными отложениями (изменчивостью по вертикали в рамках рассматриваемой задачи можно пренебречь), является ярким примером, по фронту намыва можно выделить выраженные закономерности изменения его параметров (см. рис.2) [2, 3].

Поиск оптимального решения по определению разбиения объектов на группы с учетом внутренних и внешних факторов предлагается выполнять в несколько этапов. На первом - производится нормализация значений локальных критериев, т.е. преобразование натуральных значений факторов в безразмерные.

I                             II                     III

Рис. 2а. Изменение гранулярного состава отложений по длине откоса намыва: I, II, III - зоны гидроотвала

1-

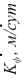
11 -

9 -

7 -

2- 73—^

• 1-    коэффициент фильтрации;

• 2-    плотность;

• 3-    естественная

влажность

Рис. 2б. Зависимости водно-физических свойств намывных песков.

Пусть имеется матрица наблюдений X размерностью n х m , строки i которой соответствуют пробам, i = 1, 2, …, n , а столбцы j содержат конкретные показатели, j = 1, 2, …, m , полученные в точке наблюдения i . В таком случае по каждому из столбцов необходимо провести такое математическое преобразование данных, при котором параметр представляется не в абсолютных (градусах или г/см³), а в некоторых безразмерных единицах, характеризующих относительное значение признака. При таком представлении данных можем сравнивать влияние отдельных параметров наблюдения на степень различия объектов

В общем случае при центрировании (нормализации) значений используется преобразование вида:

ij

xtj xjo

Aj

где x_i j – натуральное текущее значение i – показателя j-го фактора;

• x j _o – натуральное значение нулевого уровня j-го фактора;

• λ j – интервал варьирования j-м фактором, натуральное значение;

Рассмотрим преобразование, в котором в качестве нулевого уровня выступает среднее значение, а в качестве интервала варьирования – Евклидово расстояние.

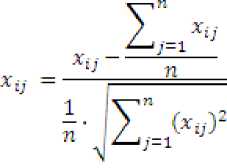
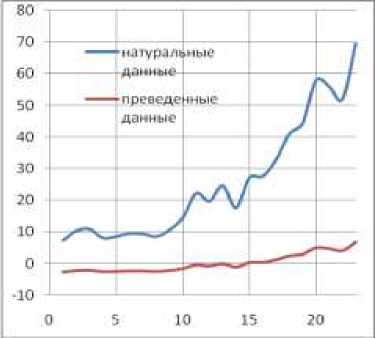
Для примера произведем нормирование показателей грансостава намывных отложений гидроотвала «Шамаровский Лог» (см. табл. 1). Как видно на рис. 3 при данном виде приведения данных принципиально функциональная зависимость не изменяется, однако существенно уменьшается значимость «выбросов» величин.

Натуральные значения грансостава

Таблица 1

№ пробы	> 0,25 мм, %	0,25 – 0,1 мм, %	0,1 – 0,05 мм, %	0,05 – 0,01 мм, %	0,01 – 0,005 мм, %	< 0,005 мм, %
1	1,12	41,21	15,67	30,79	4,02	7,19
2	0,79	30,97	14,78	34,13	9,01	10,32
3	0,64	29,79	10,81	40,89	7,02	10,85
4	0,54	20,11	13,62	49,56	8,16	8,01
5	0,4	15,7	11,4	54,9	9,07	8,53
6	0,32	11,8	10,7	61,65	6,08	9,45
7	0,25	9,81	11,01	57,78	11,8	9,35
8	0,22	7,34	12,3	61,35	10,3	8,49
9	0,12	5,27	4,22	68,1	11,7	10,59
10	0,02	0,89	5,08	65,19	14,3	14,52
11	0	0,65	2,1	32,12	42,98	22,15
12	0	0,43	1,78	32,34	45,78	19,67
13	0	0,21	1,59	23,78	49,87	24,55
14	0	0,31	1,91	29,76	50,45	17,57
15	0	0,2	1,62	21,2	49,92	27,06
16	0	0,15	1,65	22,78	47,89	27,53
17	0	0,1	1,6	20,3	45,24	32,76
18	0	0,05	1,55	14,82	42,59	40,99
19	0	0,1	1,2	12,8	41,56	44,34
20	0	0,09	0,14	12,5	29,45	57,82
21	0	0,05	0,34	11	32,7	55,91
22	0	0,01	0,02	10,02	37,98	51,97
23	0	0	0	8,68	21,81	69,51

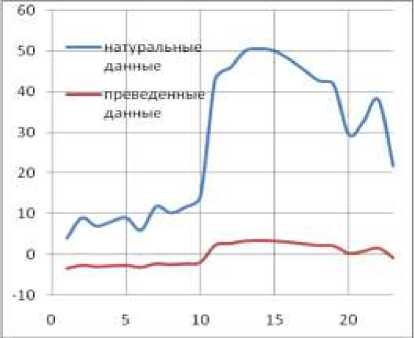
Рис. 3. Изменение содержания частиц диаметром от 0,01 до 0,005 мм (слева) и менее 0,005 (справа) по фронту намыва в натуральном и приведенном виде.

Обработка и представление экспериментальных данных позволяет в дальнейшем вести статистическое сравнение проб, которое необходимо при районировании техногенных массивов. При построении сетей инженерно-геологических исследований определение статистических мер позволяет в оптимизированной форме осуществлять сгущение точек опробования.