Способы работы с пропущенными данными для задач кредитного скоринга

Задача кредитного скоринга является важнейшей составляющей процесса кредитования в банковской сфере. На основе результатов моделей кредитного скоринга, среди прочего, рассчитывается средний уровень вероятности дефолта (Probability of Default – PD) – одного из факторов, участвующих в расчете норматива достаточности капитала в соответствии с требованиями Базельского комитета [1] в рамках продвинутого подхода на основе внутренних рейтингов (A-IRB). Модель напрямую влияет на предсказанные значения долгосрочной вероятности дефолта, что может приводить к существенным изменениям требований к резервному капиталу банка.

Перед банками стоит задача построения высококачественной модели для решения задачи кредитного скоринга, так как это позволит, во-первых, сократить объемы резервов по требованиям Центрального Банка, во-вторых, более качественно определять вероятность невозврата кредита на уровне отдельного заемщика, и, в-третьих, ранжировать пулы клиентов по величине риска для формирования кредитного портфеля.

Одной из важнейших составляющих задач кредитного скоринга является способность ранжирующего алгоритма выполнять сегментацию клиентов. Интерпретируемая сегментация на платежеспособных и неплатежеспособных заемщиков является конечным результатом, в то время как неинтерпретируемая сегментация в пространстве латентных признаков может быть более ценной с точки зрения ранжирующей способности финальной модели ранжирования заемщиков. Под латентными признаками можно понимать некоторую комбинацию исходных признаков заемщика. Выделяемые сегменты используются либо в качестве предиктора в моделях машинного обучения любой сложности, либо в качестве разделителя портфеля клиентов. Они позволяют оценивать параметры отдельной модели для каждого сегмента, что улучшает качество кредитного скоринга по сравнению с использованием единой модели для всего портфеля заемщиков.

Отдельно стоит упомянуть распространенную проблему пропущенных значений в данных при построении той или иной модели. Для банковского скоринга пропуски в данных чаще всего означают, что у потенциального клиента нет кредитной истории на момент оценки его кредитоспособности. Также возможны случаи технических ошибок и потерь важной информации, касающейся кредитной заявки. Все такие случаи, тем не менее, должны обрабатываться моделью кредитного скоринга с учетом сегментного уровня риска, для чего используются различные способы восстановления пропущенных значений.

В данной работе были рассмотрены основные способы работы с данными, содержащими пропущенные значения, применительно к задаче кредитного скоринга. Дополнительно для решения данной задачи был апробирован подход восстановления пропусков с помощью генеративных состязательных нейронных сетей (Generative Adversarial Networks), предложенный в работе GAIN: Missing Data Imputation using Generative Adversarial Nets [1].

Под моделью кредитного скоринга в данном случае понимается классическая для банков модель логистической регрессии над набором факторов. Для чистоты эксперимента набор факторов фиксирован и не меняется от сегмента к сегменту. Таким образом возможно оценить чистый эффект от применения нейросетевых архитектур, выделяющих сегменты в латентном признаковом пространстве.

Задача кредитного скоринга рассматривается как частный случай задачи бинарной классификации, в которой целевое событие – факт реализации дефолта. Факт дефолта определяется следующим образом:

– заемщик признается находящимся в дефолте, если суммарная длительность просроченных платежей по его кредитным обязательствам превышает 90 дней в течение 18 месяцев с начала наблюдения;

– заемщик признается не находящимся в дефолте, если в течение 18 месяцев с начала наблюдения для него не было зафиксировано суммарных просрочек платежей по кредитным обязательствам, превышающих 90 дней.

Метрикой качества алгоритмов принимается коэффициент Джини [5], который непосредственно связан с CAP-кривой (Cumulative Accuracy Profile) [6].

CAP-кривая показывает, какой части дефолтных клиентов модель присваивает относительно худший скоринговый балл. Соответствующий CAP-кривой коэффициент Джини ( Gini ) вычисляется следующим образом:

„. . Площадь между модельной САР-кривой и диагональю (jim =---------------------------------------------------------------.

Площадь между САР-кривой идеальной модели и диагональю

Коэффициент Джини варьируется в интервале [0, 1], где 1 – идеальная модель, 0 – случайные результаты (аналогичные подбрасыванию монеты).

Способы восстановления пропущенных значений в аспекте решения задачи кредитного скоринга

Существует множество способов работы с пропусками в данных, многие из которых применяются на практике при построении моделей кредитного скоринга. Рассмотрим наиболее популярные из них, добавив к этому списку наиболее современные разработки по интеллектуальному восстановлению пропусков с использованием нейронных сетей.

Выделение пропусков в отдельную категорию

Самый простой с точки зрения реализации метод – трактовка пропусков в определенных признаках клиента как отдельных классов наблюдений. Например, для фактора «Наибольшая сумма просроченной задолженности за последний 12 мес.» пропуск чаще всего означает, что кредитной истории для данного клиента нет (в отличие от значения «0», которое означает, что история есть, но клиент в просрочку не выходил).

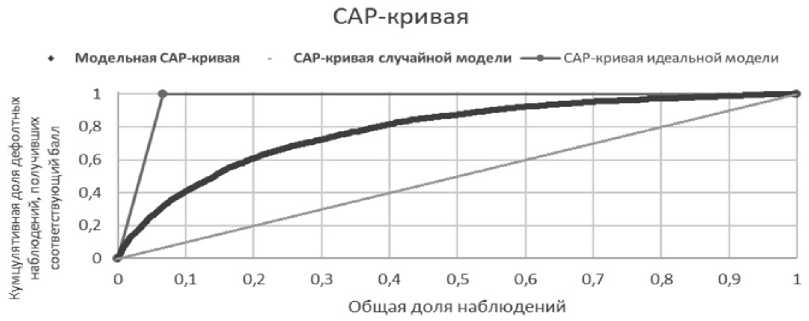
Рис. 1. Пример CAP-кривой

Именно для задачи кредитного скоринга данный метод очень удобен и работает для большого числа факторов, отвечая одновременно и требованиям к качеству моделей и регуляторным требованиям специальной обработки пропущенных значений.

Заполнение пропусков статистическими показателями – средним, медианой

Наиболее популярный способ восстановления пропущенных значений – заполнение средним значением по данному фактору. На практике чаще используют заполнение медианным значением, так как медиана является более устойчивым показателем к выбросам в данных. Заполнение средним используется, когда отсутствует некоторое априорное понимание экономического смысла пропущенных значений. Например, пропуск в признаке «Средняя заработная плата за последние 12 мес.» может означать, что человек не предоставил соответствующих документов, ошибку в системе, что он начал трудовую деятельность менее 12 мес. назад и т.д. В данном случае мы не можем надежно утверждать, что все пропуски в данном признаке будут согласованы между собой с точки зрения экономического смысла, следовательно, наиболее логичный вариант их восстановления – заполнение средним значением. Таким образом работа модели не будет искусственно ухудшаться из-за неправильной трактовки пропусков.

Заполнение пропусков с помощью вспомогательных моделей

В данной работе рассмотрим способ восстановления пропусков с помощью GAN модели, однако, стоит отметить, что существуют также варианты восстановления пропусков с помощью отдельных моделей кластеризации, классификации и регрессии (в зависимости от типа признака).

Основой модели GAIN служит пара нейронных сетей, позволяющих с высокой достоверностью восстанавливать исходное наблюдение (например, изображение) после прохода его векторного представления через последовательность слоев, сжимающих и разжимающих это векторное представление. После процесса обучения данная архитектура способна генерировать наблюдения целиком, либо, что для нас более интересно, восстанавливать пропущенные части целого наблюдения (пропуски по некоторым факторам).

Подробно архитектура модели описана в работе [1], ниже приведено ее схематичное изображение (рис. 2).

Результаты реализации рассмотренных алгоритмов

Для тестирования указанных выше алгоритмов использовались данные заем-щиков-юридических лиц топ-5 крупнейших банков РФ (300 тыс. наблюдений), для которых строилась модель кредитного скоринга. При этом, анализируемые признаки для тестирования алгоритмов выбирались таким образом, что восстанавливались только пропуски, экономическая природа которых неочевидна.

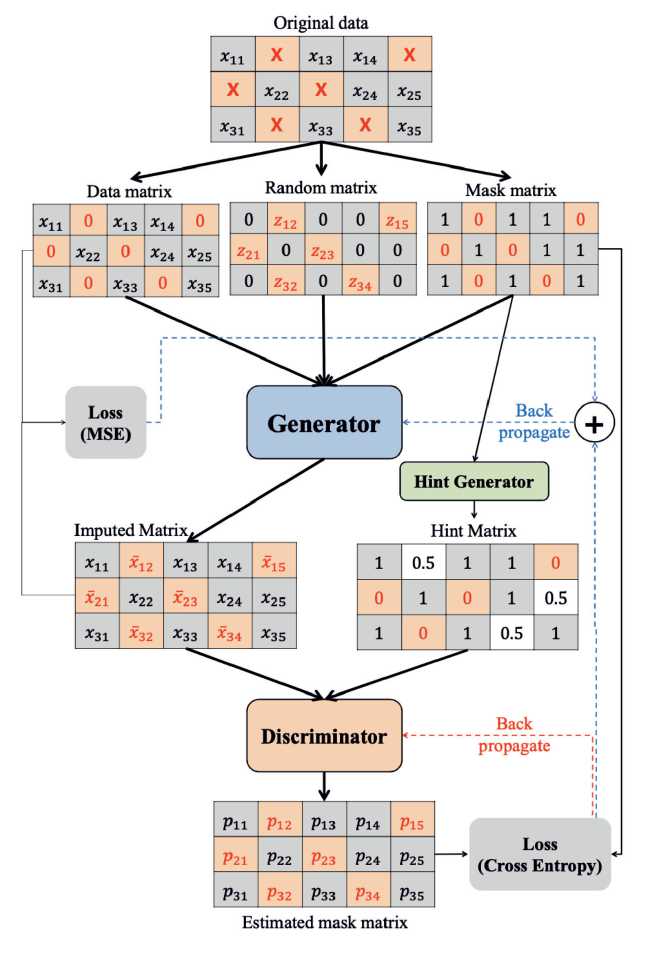
Рис. 2. Архитектура модели GAIN