Способы расчета границы зоны видимости поверхности Земли с космического аппарата при различной ориентации и размерах телесного угла наблюдения

Задача, связанная с определением наблюдаемой зоны поверхности Земли с космического аппарата (КА) при различной ориентации и размерах телесного угла наблюдения, является одной из распространенных задач баллистико-навигационного обеспечения определенного класса КА. В частности, к таким космическим аппаратам можно отнести КА связи и КА, используемые для визуального наблюдения поверхности Земли и околоземного про

странства.

Основным результатом решения данной задачи являются координаты замкнутой линии - границы зоны наблюдаемости (ЗН), которые могут быть вычислены с использованием предлагаемого в данной статье алгоритма.

При описании алгоритма используются следующие обозначения и допущения. В качестве математическим представлении поверхности Земли принят двуосный эллипсоид вращения в гринвичской системе координат (ГСК) (0, x_G , y_G , z_G ) . Уравнения этого эллипсоида в матричной форме может быть представлено в виде

q G • A G ' q G = ¹ ,                     ⁽¹⁾

где A G =

" 1/ aa

1/ a¹

1/ b a

x G

^q g = y G - соответ-

< z^G

ственно матрица квадратичной формы размерности 3 x 3

и 3-мерный вектор координат x_G , y_G, z_G в ГСК; а , b -соответственно размеры большой и малой полуосей эл

липсоида.

Для упрощения и наглядности математических преобразований в данной статье используются четыре специальных декартовых системы координат (СК), начала которых совпадают и находятся в центре масс КА, в точке с координатами ( xka, yka, zka ) в ГСК.

Навигационная орбитальная система координат (НОСК) (0, x_N , y_N , z_N ) - это такая СК, в которой ось Oz N совпадает с направлением линии от центра ГСК к центру НОСК, ось Ox_N перпендикулярна оси Oz N и лежит в плоскости, содержащей центр Земли и вектор скорости КА, ось Oy_N дополняет систему до правой системы координат. Направление оси Ox N выбирается по условию, что угол между осью Ox N и вектором скорости КА V = (Vxka , Vyka , Vzka ) в ГСК минимален. Формула перевода координат из ГСК ( q_G ) в НОСК ( q_N ) имеет следующий вид:

q N = M n • q G - M n • qka ,             (2)

где qka = ( xka , yka , zka ) T , M_N - соответственно радиус вектор КА в ГСК и матрица направляющих косинусов,

элементы mN (i, j), i, j = 1,3 которой вычисляются по формулам mN(2,1) = d 1/d, mN(2, 2) = d2/d, mN(2, 3) = d3/d, mN (3,1) = xka / R, mN (3, 2) = yka / R, mN (3, 3) = zka / R, mN (1,1) =

= mN (2, 2)zka / R - mN (2, 3)yka / R, mN (1, 2) = mN (2, 3)xka / R - mN (2,1)zka / R, mN (1, 3) = mN (2,1)yka / R - mN (2, 2)xka / R, d 1 = yka • Vzka / R - zka • Vyka / R, здесь d 2 = zka • Vxka / R - xka • Vzka / R, d 3 = xka • Vyka / R - yka • Vxka / R, d = V d 12 + d 22 + d 32, R = xka2 + yka2 + zka2 '

Конструкторская декартовая система координат (КСК) (0, x K , y_K , z_K ) имеет оси, ориентированные по осям симметрии КА. Эта система координат используется для задания ориентации системы наблюдения КА. Перевод координат из КСК q _K в НОСК q_N осуществляется по формуле

q N    ^M K • q K ,                   ⁽³⁾

в которой матрица направляющих косинусов M K зависит от ориентации осей КА в НОСК.

Предполагается, что система наблюдения КА обеспечивает обзор поверхности Земли и околоземного про

странства в пределах конуса, имеющего определенные угловые размеры. В качестве параметров, определяющих размерность и ориентацию конуса наблюдения, можно взять телесный угол конуса, равный 2 у , где Y - угол между центральной осью и образующей конуса; азимут оси конуса а - угол, отсчитываемый от оси Ox_K против часовой стрелки в плоскости Ox K y K ; угол места в - угол, отсчитываемый от плоскости Ox K y K против часовой стрелки в направлении от оси Oz_K в КСК.

Конусная система координат (КнСК) (0, x_KN , y_KN , z_KN ) - система координат, в которой ось Oz_KN лежит на фокальной оси конуса и направлена от центра Земли. Ось Ox_KN перпендикулярна оси Oz_KN и лежит в плоскости, заданной в КСК уравнением x K cos а - y K sin а = 0 . Ось Oy_KN дополняет систему до правой. Формула перевода координат из КнСК q _KN в КСК

q _K имеет вид

гд^{е M} KN

q K " cos а cos в sin а cos в _ч - sin в

= ^M KN • q KN ^,

- sin а cos а sin в² cos а sin а sin в

0 cos в

Плоскостная система координат (ПлСК) (0, xP, yP, zP) - это такая система координат, в которой ось OzP совпадает с осью OzKN . ПлСК в начальном положении (ю = 0) полностью совпадает с КнСК. При значениях ю ^ 0 ось OxP сориентирована таким образом, что угол между векторами OxKN и OxP в КнСК равен ю, а ось OyP дополняет систему до правой. Формула перевода координат из ПлСК qP в КнСК qKN имеет вид qKN MР (ю) ' qP ,                  (5)

^ cos ю sin ю 0 ^

где M_P ( ю ) = - sin ю cos ю 0

0       0    1

Формулы обратного перевода координат для указанных четырех систем координат получаются как решение уравнений (2)^(5) относительно векторов qG, qK , qKN , qP.

Учитывая введенные обозначения, можно утверждать, что искомая ЗН должна быть образована пересечением эллипсоида вращения и конуса. Следовательно, ЗН есть решение системы уравнений qKN ' AKN ' qKN - 2 ' qKN ' AKN ' qCKN + qCKN ' AKN ' qCKN = 1

-                                                                                    (6)

xKN + yKN - tg2Y' ZKn = 0, которые представлены в КнСК. Это несложно сделать с учетом введенных выше систем координат. В частности, первое уравнение - уравнение эллипсоида - имеет такой вид благодаря тому, что матрица квадратичной формы эллипсоида в КнСК имеет вид AKN = DT • AG • D, где D = MN • MK • M KN - матрица перевода координат из ГСК в КнСК, а вектор координат qCKN центра эллипсоида в КнСК можно получить по формуле qCKN = DT (-qka ) .

Приведение указанных уравнений в КнСК позволяет записать уравнение конуса в канонической форме, что упрощает совместное решение системы.

В реальной обстановке при различной ориентации осей КА и оси конуса в КСК часть образующих конуса могут не пересекать поверхность эллипсоида. Это приводит к тому, что для определения ЗН необходимо решать описанную выше задачу при некоторых ограничениях. Все решения системы (6) делятся на два типа. Одни решения принадлежат видимой (наблюдаемой с КА) зоне - это множество V, другие - и теневой (не наблюдаемой с КА) зоне - это множество Т. В итоге определение границы ЗН сводится к нахождению всех решений системы уравнений qKN ' AKN ' qKN — 2qKN ' AKN ' qCKN + qCKN ' AKN ' qCKN = 1

- x KN + y KN = tg² Y' Z KN ,                                       ⁽⁷⁾

(xKN , yKN , ZKN ) G V • где Akn = MP (ю)AG • MP (ю), здесь MP (ю)T - транспонированная матрица MP (ю), вследствие ортогональности обратная к ней.

Множество V состоит из точек (xV, yV, zV), координаты которых в ГСК удовлетворяют условию того, что данная точка является ближайшим решением к точке (xka, yka, zka) системы уравнений x - xv _ y - yv

x_V - xka  у у - yka

Z ^- Z y z_V - zka

2 2 xVyV “+ 2 aa zV- = 1 b2

Задача определения границы ЗН сводится к определению координат точек границы - решений системы уравнений (7). Для этого необходимо решать систему (6) и при этом контролировать степень пересечения конуса и двуосного эллипсоида.

Далее через фокальную ось конуса будем проводить всевозможные плоскости. Каждая из плоскостей, определяемая заданной матрицей перехода M P ( ю ) в КнСК, будет содержать сечение эллипсоида, при этом возможны случаи отсутствия пересечения с эллипсоидом (рис. 1). Решение общей задачи сводится к построению этих плоскостей и определению координат точек пересечения эллипсоида и образующих конуса, лежащих в данной плоскости. Количество плоскостей и их «равномерность» относительно угла разворота относительно фокальной оси конуса определяет точность линии границы ЗН. Вне зависимости от количества учитываемых плоскостей они должны быть расположены равномерно относительно вращения вокруг фокальной оси конуса. Это означает, что углы между любыми двумя соседними (с точки зрения вращения) плоскостями должны быть одинаковыми.

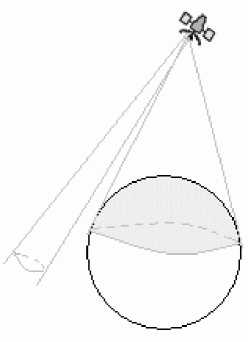
Рис. 1. Сечение Земли. Отсутствие пересечения

Дальнейшее решение задачи будем производить в плоскостях, заданных уравнением y_P = 0 в ПлСК для выбранных значений ю . Вначале нужно определить, пересекает ли данная плоскость эллипсоид. Затем в данной плоскости необходимо определить, пересекает ли сечение эллипсоида образующие конуса КС и KD (рис. 2).

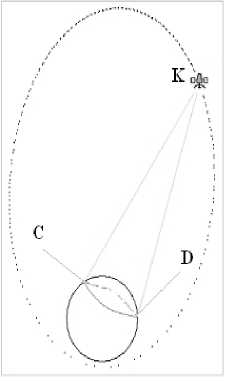
Рис. 2. Определение ЗН

Задача определения координат точек C и D сводится к решению следующей системы уравнений:

q p "  A p "  q p ^{- 2} q p "  A p "  q cp ⁺ q cp "  A p "  q cp = 1,     (g)

. X p = ± tg Y z p , y p = 0.

Далее будем решать уравнение (8), проверяя принадлежность точек решения к множеству V , Проведя простое преобразование, получим первое уравнение в сле

дующем виде:

a _m [1] x ² + 2 a _m [3] x • z + a _m [9] z ² - 2 c 1 • x - 2 c ₃ • z + d = 0 , где { a _m } - матрица эллипсоида вращения в ПлСК;

c = a m[1] xc + a m[2] yc + a m[3] zc, c з = a m[7] xc + a m[8] yc + a m[9] zc, d = a m[1] xc2 + 2 a m [2] xc • yc + a m[5] yc2 + +2am[3]xc • zc + 2am[6]yc • zc + am [9]zc2 -1. Итак, система уравнений примет вид am [1]x2 + 2am [3]x • z + am [9]z2 - 2c1 • x - 2c3 • z + d = 0, . x = ±tg уz, что позволяет, подставив второе уравнение в первое, получить квадратное уравнение относительно z:

( a _m [1]tg² Y⁺ 2 a _m [3]tg Y⁺ a _m [9]) z ^{2 -}

образующих конуса, лежащих в данной плоскости, пересекает Землю, Это означает, что хотя бы одна из двух образующих конуса, лежащих в данной плоскости, пересекает поверхность двуосного эллипсоида,

Для некоторых задач необходимо контролировать, пересекает ли фокальный луч конуса поверхность эллипсоида, Для этого в ПлСК нужно определить, имеет ли уравнение a J1] x ² + 2 a J3] x • z + a _m [9] z ² - 2 c 1 • x - 2 c ₃ • z + d = 0 решение при условии x = 0 , Если c ₃ • c ₃ - d • a _а [9] >= 0 , то фокальный луч пересекает поверхность Земли,

В случае пересечения одной из образующих поверхность эллипсоида решение в ПлСК имеет вид xpLSK = t1 • M - xc, yFLSK =- yc, zpLSK = M - zc,

t* • c + c3 + 4Discr(t*)/4 где M =----—------;----- a „ [1](t1)2 + 2 a а [3]t1 + a „ [9]

. *

; t 1

= min( t 1 , - tg y ) ^-

тангенс угла наклона образующей, в случае если образующая конуса не пересекает поверхность Земли t * -тангенс наклона касательной, проведенной из центра масс

- 2( c 1 • tg Y+ c ₃) z + d = 0       -

Запишем дискриминант данного уравнения, Только вместо константы tg y будем использовать переменную t ■ Получим

Discr( t ) = 4 X

^X ( ( c ! ^- a _m [1] d ) t ^{2 -} 2( a _m [3] d ^- c • c 3 ) t + c 3 ^{2 -} d • a _m [9] ) ■

Значения параметра t , при которых Discr( t ) = 0 , будут равны тангенсам наклона тех прямых, которые являются касательными к сечению двуосного эллипсоида в данной плоскости, При этом если Discr( t ) <  0 , то это означает, что данная плоскость не пересекает поверхность двуосного эллипсоида Земли,

В случае если

A = ( a _m [3] d - c • c 3 )² - ( c, - a _ю [1] d )( c 3 ² - d • a _ю [9]) >  0 ^,то данная плоскость будет пересекать поверхность земли и переменные t 1 , t ₂ будут соответственно меньшим и большим из двух чисел:

aа [3]d - c1 • c3 ± A c" - a а [1] d '

Если выполняется хотя бы одно из условий: tg Ye ( - 1 ₂, - 1 1 ) или tg Ye ( t 1 , t ₂) , то хотя бы одна из

КА к поверхности Земли в данной плоскости, Для второй образующей решение может быть получено по той же формуле, только вместо параметра t * нужно использовать параметр t * = max( 1 ₂, tg y ) ,

Рассмотренную процедуру вычислений необходимо

произвести для всех принятых к учету плоскостей, Далее необходимо перевести координаты граничных точек в ГСК, Для этого построим матрицу перевода из ПлСК в ГСК, Координаты точек границы в ГСК, полученных при сечении эллипсоида плоскостями в КнСК можно вычислить по формуле

(х xGSK yGSIK ч zGSK

X

= mD • mp T

(х xpLSK ypLSK v zpLSK

X

,

Точка с координатами ( x_GSK , y_GSK , z_GSK ) принадлежит поверхности Земли, Остается лишь произвести перевод координат из ГСК в геодезические координаты для даль

нейшего нанесения точек границы на карту плоской проекции поверхности Земли,

Таким образом, предложенная методика и алгоритм решения задачи позволяют получить точные результаты и существенно оптимизировать расчет зоны наблюдаемости для использования в геоинформационных системах,

THE METHODS OF ESTIMATION OF VISIBILITY ZONES ON EARTH SURFACE FROM A SPACE VEHICLE FOR DIFFERENT ORIENTATIONS AND SOLID ANGLE VALUES

The aricle considers a problem of estimation of visibility zones on Earth surface from SV with orientable axis of antenna with given diagram of visibility solid angle. The methodology and algorythm of exact and optimal calculation of mentioned zones are describedfor use during graphic mapping onto electronic maps.