Способы синтеза и оценки технологических схем узловой и агрегатной сборки в самолётостроении

ектирования конкретной производственной деятельности при представлении сборки в виде модели как ориентированного графа.

В рамках решения этой задачи выбора оптимального по ряду критериев проекта ТП в работе рассматривается проблема определения, синтеза и оценки последовательности операторов преобразования сборочно-монтажного пространства. Так как сложная задача сборки и монтажа узлов и агрегата в целом подразумевает использование достаточно большого количества операций со специфическим набором инструмента и оснастки, которые должны быть не независимыми, а объединенными иерархически: некоторый оператор отражает факт принадлежности компонентов, рассматриваемых в задаче, конкретному множеству. Однако, сколько бы уровней рассмотрения ситуации ни понадобилось при решении поставленной задачи, отражения ее компонентов в виде высказываний, моделей и т.д., в конечном счете они сводят семантику логических высказываний от содержательной интерпретации моделей к констатации наличия определенных физических свойств у узла, агрегата, системы, а также выбора процесса сборки.

В задачах проектирования ТП необходимо совместить аналитическую взаимосвязь между параметрами уравнения и параметрами решения, одновременно с этим выразить эту взаимосвязь в виде алгоритма управляющих воздействий на системы разного рода. Таким образом, можно совместить в параметрическом виде исходное уравнение и его решение, получив параметрическую структуру, изменение которой с течением времени анализируется для получения оптимального параметрического пространства решений, в котором выбираются устойчивые состояния ТП.

Рассмотрим параметрические формы a 1 ( A₁ , A ₂, t ) и a ₂ ( A ₃, A ₄, t ) , описывающие состояния ТС:

*

w b ⁽ t ) = A + A 2 w b ⁽ t );

w*(t) = A3 - A4 w*2(t),

*...*

где w b – динамика выполнения операции; w – динамика подготовки производства для выполнения операции; А1 – параметр ресурсов; А2 – параметр эффективности; А3 – параметр, характеризующий индекс качества операции; А4 – параметр, характеризующий неустойчивость по некоторому критерию операции (фактор рисков).

Уравнение, описывающее состояние ТС, представляет частный случай уравнения Риккати, которое в первом приближении решается в квадратурах, причем считаем, что w(t) и wb(t) -наблюдаемые фазовые координаты соответствующих векторов состояний в начале или в конце фиксированного промежутка времени наблюдений за группой a 1 ( A₁ , A ₂, t ) , a ₂ ( A ₃, A ₄, t) .

В качестве достаточных приближений значений для w(t) и wb(t) в детерминированных условиях процесса выбираем:

w_b X t ) = tg ⁽V ^AAt ) 4 A ^;      (3)

• V    A 2

w * ( t ) = th ( д/ A₃A₄t ) -y^-       (4)

• V    A 4

Выбор условий для решения уравнений (1) и (2), составленных для wb(t) и w(t) , должен удовлетворять форме уравнений в определённой метрике t. Однако формы решения могут свидетельствовать о неучтённых факторах при описании состояния ТС, влияющих на неустойчивую природу взаимодействия учитываемых факторов. Тогда получаемые решения имеют вид нелинейных неустойчивых кривых, имеющих особые точки, которые можно отнести к интервальным системам решений задач оптимизации ТП в дискретных сборочных пространствах. Это может быть связано с изменением маршрутов или содержания процессов сборки, вследствие чего вводятся дополнительные связи между компонентами производства агрегата. При более точных условиях измерения фазовых координат wb(t) и w(t) в этом случае исходные уравнения имеют вид

W b ( t ) = A ₁ + A ₂ w b ( t ) + A ₅ sin[ w b ( t ) t +

.. *                                                  .. *           (5)

Ф ь o ] a ( t ) - A 5 cos[ w_b ( t ) t + ф ь ₀] P ( t );

— w (t) = A + A4w*2(t)- wb2(t)A, +

*

A 7 sin[ w * (t ) t + Ф _{ь q} ] ^ ( t ) - A 7 cos[ w * ( t ) t + (6)

* — — +Ф ь q ] P ( t ),

* — — где a ( t ) - функция, учитывающая характер условий реализации конструкторско-технологической информации. После подстановки w_b ( t ) и w ( t ) в уравнение, описывающее характер динамики сборочных потоков по значениям перемен

*

ных функций a ; р ( t ) , где w b ( t ) , w * ( t ) характеризуют динамику изменения условий для последующих процессов сборки, ,получаем параметры характеристик устойчивости операций сборки.

Сгруппировав слагаемые ряда в уравнениях (5)-(6) по степеням t : t , 1 ³ ,_{-- —} , получаем несколько уровней классификации состояния системы ТП сборки. Получение решения w(t) в виде ряда по степеням t определяет, какие параметры влияют на форму кривых w b ( t ) и w ( t ) , и позволяет формировать управляющие воздействия для получения нужных форм w b ( t ) и w ( t ) . Форма фазовой координаты w b ( t ) в данном случае является искомой для текущего фазового пространства состояний сборочных позиций.

Такой подход позволяет анализировать большое количество элементов сборок с варьируемым числом функциональных аргументов (операторов преобразований пространства сборки), или предикатов как переменных состояния из соответствующих областей определения оптимальных сборочных схем:

P(x, y) > P(x, y, s) ,…,Р(x,y,s,t,n).     (1)

В общем случае при сборке n-местный предикат Р последовательно заменяется n+1 местный по технологической переменной состояния x,y,s,s,…,n, ассоциированной с этим предикатом Р. Для построения моделей агрегатно-сборочного производства применима аксиома преобразования сборочно-монтажного пространства одного из двух типов в виде:

Pr (x, ^1) • (P (xi, ^1) = 52) ^ Q (x, S2), (2) где P,Q e P, F e F, 81,82 E S.

Соотношения могут быть записаны в более общей форме. Однако, можно считать, что они имеют следующий смысл: для того, чтобы применить оператор F в ситуации S1, прежде всего необходимо, чтобы выполнялось условие P , т.е. это начальное требование для применимости оператора F. Теперь, после применения оператора F, полученное состояние характеризуется предикатом W. Под буквами Р и W в приведенных записях мы будем иметь в виду, что эти символы обозначают подмножество множества предикатов Р. Так например, начальное условие Р может быть длинной конъюнкцией предикатов Р = Р1, Р2... Рn, которая полностью характеризует все условия применения оператора F в ситуации S1. Таким образом, Р – это своего рода начальные условия, а W - конечные условия по отношению к оператору A. В общем виде, т.е. независящими от конкретного состояния S1, аксиомы могут быть записаны следующим образом:

V S { P ( x , S ) ^ Q ( x , F ( x , S )) } , (3) где мы воспользовались подстановкой F(х,S) вместо S₂, тем самым исключив обозначения двух конкретных состояний. В этом выражении S соответствует начальному состоянию S₁, а F(х,S) – конечному состоянию S₂.

Для описания начальной ситуации используются схемы вида:

D(x, S_H, А), (4) где D g P , S H g S, x G A.

В этом случае SH – конкретное начальное состояние, х – элемент множества узлов, А – константа, имеющая существенное отношение к начальной ситуации. Для начальной ситуации предикат Р не обязательно будет двухместным предикатом. В общем случае он может быть произвольным n-местным предикатом с любым числом аргументов. Таким образом, каждому конкретному условию соответствует целый ряд получаемых соединений узлов - констант в свою очередь D может представлять собой последовательность конъюнкций такого рода предикатов. Сформулировав теперь задачу в формальной записи, решаем вопрос, существует ли конечное состояние S, для которого выполняется условие

k

^S ( x , ^Sk Ь у ^Si , или ( ₃ S_k ) { S ( x , S k ) } ; (5) i = 1

Теоретическое обоснование решения задачи сводится к доказательству теоремы на основе аксиом исчисления последовательности операторов преобразования. с указанием последовательности операторов преобразования вида:

Sk = F1 (x, F2 (x, … , Fn-1 (x, Fn (x, SH )))) = F1·F2 … Fn (x, SH). (6)

Последовательность функционалов F1, F2,... Fn представляет суперпозицию операторов, которые последовательно применяются к начальному состоянию и переводят его в конечное. Перед исполнением оператора сначала проверяется истинность предикатаW, связанного с результатом действия Fi. Если оператор Fi выполнен верно, исполняется оператор Fi+1. Если получен отрицательный результат действия по оператору Fi+1, повторяется итерация для Fi. Расчеты выполня-

ются по алгоритму, учитывающему влияние входов различной длины и содержания на качество процессов сборки. Базовая схема такого алгоритма решения логических задач в исчислении последовательности операторов преобразования достаточно высокая. Для определенности процесса преобразований необходимо точно описать начальную ситуацию для того, чтобы можно было применять те или иные аксиомы. Результаты работы являются основой для развития интеллектуальной системы автоматизированного проектирования технологических процессов сборки узлов и агрегатов летательных аппаратов.

Таким образом, полученные вероятностнодинамические модели могут быть использованы в прикладных задачах разработки реальных проектов сборки, где число элементов собираемых узлов всегда конечно, но не определено однозначно по фактическому состоянию в динамике на множестве рабочих мест исполнителей, а операции сборки могут быть описаны вероятностнодинамическими моделями.

Например, для стационарного состояния I. Требуется вычислить собственные значения матрицы. В линеаризованной системы, что сводится к вычислению коэффициентов b_ij. Получаем

b 11

b 21

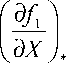
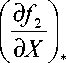
= 0

= K1

^b 12

^Ь 22

(5^ 115 Y )

= K ₃ B

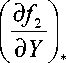
= 0

где звездочка означает, что численные значения производных следует брать при

KB KD

* =        Y * =

1 K2 , 1 K2

Из характеристического уравнения (13) находим

A = + 4K1K3 DB . (8)

Это означает, что стационарное состояние 1 нейтрально устойчиво и, когда система под действием слабого возмущения покидает это состояние, она переходит на периодическую траекторию, размеры которой определяются величиной возмущения, и описывает ее с циклической частотой, равной A = + ^ K ₁ K ₃ DB (двигаясь в пространстве состояний, где значения переменных растут от начала, всегда по часовой стрелке).

Стационарное состояние II. Производя анализ, аналогичный проделанному выше, но вычисляя теперь значения производных в точке Х^*₁₁ =0, Y^*₁₁ =0, получаем

bu = K 1 A    b12 = 0

b 21 = 0   b 22 = - K 3 B

Характеристическое уравнение в этом случае имеет вид

(K 1 D - 2 ) (K 3 B + 2 )=0      (10).

и собственные значения оказываются равными 2 1 = K 1 D >0 и 2 ₂ = - K 3 B <0.

Стационарное состояние (0,0) неустойчиво.

Так как рассматриваемая система функционирует в пространстве состояний переменных Х,Y, то замкнутые траектории, соответствующие периодическому режиму, имеют основной период, определяемый по формуле

T = f

dX f (X, Y, k 1, k 2, k 3, A, B )

При этом k1, k2, k3, D, B учитывают скорости протекания реальных процессов в системе и показатели, характеризующие систему, которые разбиваются в нашей системе на два уровня (проектный и производственный).

При постановке задачи выбора оптимальной структуры модели технологического процесса (ТП), принимая во внимание сложность разработки структуры ТП и технологических схем для стохастичных ТП, перед формализованной постановкой задачи уточним ее содержательную формулировку следующим образом. Каждый ТП можно охарактеризовать набором приписываемых ему структурных компонентов для моделирования текущего режима, а также весовыми характеристиками относительной важности этих компонентов в множестве структур моделей при учете текущего режима функционирования. Глобальная цель оптимизации структуры ТП — устранение неадекватности всех формализованных процедур, применяемых при разработке систем управления. Оптимизация заключается в выборе такого набора элементов структурных компонентов, что после их включения в окончательно сформированную модель все неадекватности описания ТП будут ослаблены или устранены.

Имеется набор одновременно поставленных целей: включение в модель рационального числа переменных состояния, учет связей между ними, устранение неадекватности по возмущающим воздействиям и др. Выбор и реализация каждого из имеющихся средств может способствовать достижению одной или нескольких целей. Поставленным целям для каждого возможного режима функционирования назначаются оценки, позволяющие определить приоритетность того или иного элемента данного структурного компонента. Кроме того, элементам структурных компонентов ставятся в соответствие веса, определяющие степень их важности.

Из имеющегося множества структур моделей требуется выбрать такой набор, реализация которого приведет к достижению поставленных целей с учетом режимов функционирования.

Эта проблема может быть решена в рамках следующей задачи формального выбора подмножества из фиксированного множества вариантов.

Пусть задано конечное множество структурных компонентов D={D_l,...,D_m}, i=l,m, включающее непересекающиеся подмножества D_i={d_i1,...,d_ik}, конечное множество режимов функционирования L={l₁,...,l_n}, j=1,n и матрицы А⁽ⁱ⁾ размера k x n, элементы которых a_icj= ф (d i _c,l j ), i = 1,m, j = 1,n, с = 1,k, трактуются как значения с-го элемента структурного компонента D_i (строки) в режиме функционирования l_j представленном столбцом. Каждому элементу подмножества D_i множества структурных компонентов D приписывается весовая оценка to ⁰ i _c, to ⁰ i =( to °i1 ,^, to ⁰ i _k), определяющая важность элемента d_ik для формирования структуры модели ТП.

Пусть Iij — столбец с номером j матрицы А(i). Выделим в матрице А(i) какие-либо b строк и пусть множество Mbij — логически упорядоченный набор из b элементов аibj матрицы А(i), стоящих на пересечении каждой из выбранных строк с j-м столбцом Mbij={ai1j,…,aibj}, b

Иными словами, область определения Mbij, — наборы значений подмножеств подмножества структурных компонентов Di на lj, а Fbij — оценка этих наборов. Следовательно, индекс b в функции Fbij будет определять количество возможных вариантов набора элементов (подмножеств) для каждого подмножества Di структурных компонентов при lj.

Функции F^b_ij будем считать монотонными: с увеличением мощности подмножеств значение F^b_ij не убывает. Имеется набор чисел P_ij, i=1,m, j=1,n, используемый при задании ограничений снизу на значения F^b_ij. Заданы также числа л_icr, c Ф r, i=1,m, c,r=1,k, характеризующие возможную корреляцию между отдельными элементами в подмножествах D_i при l_j.

Из множества D структурных компонентов для каждого подмножества Di при lj из b вариантов необходимо выбрать подмножество Sopij ={di1j,…,dibj}, так чтобы была удовлетворена система неравенств maxFbij(Mbij) = mixaFbi.(ф (dilj),^. ф (diblj)) > Pij, i = 1,m, j = 1,n. Следовательно, пороги оптимальности Рij интерпретируются как уровни критериев оптимизации для заданных условий разработки проекта технологической системы. Каждой из поставленных целей соответствует своя функция Fbij и свой уровень критериев Рij. Чем ниже уровень критериев, тем с меньшими затратами средств достигается реализация проекта при определенных условиях производства.