Способы визуализации в математике

Образы в математике имеют большое значение. Немецкий математик, Дэвид Гильберт отмечает, что часто «математики стремятся к логически последовательной символической абстракции, пытаясь сохранить интуитивное понимание проблемы» [2, с. 17]. Другими словами, большое значение в математике имеет упрощение визуальной составляющей для популяризации и понимания азов. Это суждение основано на истории развития самой науки математики. Рассмотрим подробнее.

Так, например, в Древней Индии геометрические гипотезы имели своеобразное доказательство. Точнее само наличие доказательства было редким явлением. Когда математик сформулировал посылку, он строил фигуры, необходимые для доказательства, давал краткие комментарии и после этого писал "Смотрите!".

Предполагалось, что человек, желающий понять рассматриваемую проблему, может сделать это сам, изучив представленные изображения без каких-либо дальнейших объяснений. Например, вспомним теорему о том, что площадь круга равна площади прямоугольника, стороны которого - суть полуокружность и полудиаметр. В XVI веке, Ганеше [1], интерпретировал ее схематически (см. Рис. 1).

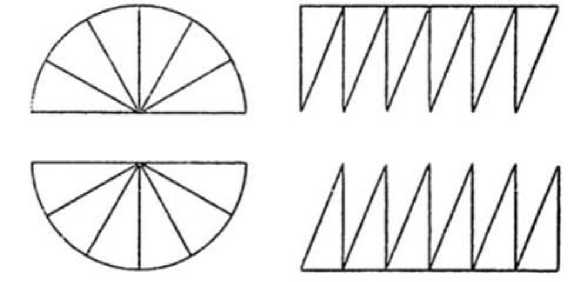
Рисунок 1 – иллюстрированное объяснение равенства площадей между кругом и прямоугольником со сторонами, равными радиусу и длине полудуги.

Известно, что до 80% информации человек получает зрительно. Физиологами и психологами доказано, что за вербально-символические функции отвечает левое полушарие головного мозга. И анализ практик обучения математическим дисциплинам в школе, показал, что учителя стараются делать больший упор на развитие логического мышления учеников – на развитие левого полушария. На это обращал внимание еще доктор педагогических наук Виктор Далингер в своих трудах. Он неоднократно поднимал проблему стабилизации и сбалансировании работы левого и правого полушарий. Им было выдвинуто предложение строить процесс обучения математики через зрительно-познавательный подход, т.е. через максимальное использование потенциальных возможностей визуального мышления. К похожему выводу пришел А. Г. Мордкович. Его труды основывались на принципе наглядности, с опорой на развитие правого полушария головного мозга. Он считает, что большое количество геометрических иллюстраций, разнообразие мягких моделей и правдоподобное объяснение материала приведет к лучшему его усвоению у учеников. Р. Артхейм [1] описал развитие визуального мышления через зрительные операции. Т.е. это своеобразная деятельность, с помощью которой обеспечивается создание и оперирование различных образов.

Визуализация в математике в основном происходит через использование графиков и диаграмм. Графики, как известно, строятся по осям X и Y и показывают зависимость каких-либо данных друг от друга. При этом видов самих графиков может быть множество. Диаграммы же демонстрируют соотношения набора данных или связи внутри набора данных. В основном строятся вокруг осей, но не всегда. Также их можно построить по секторам или полярной системе координат. На данный момент насчитывается около 60 видов диаграмм. В школе часто можно встретить временные диаграммы, Блок-схемы (диаграммы визуализации процесса) и пр. наблюдается активное использование метода мозгового штурма с визуализацией виде диаграммы или составление облака слов по определенной теме.

Другой часто встречающийся способ визуализации на уроках математики - матрицы. Сопоставляют значения внутри набора данных, но, в отличие от обычной диаграммы, отображают их в виде таблицы.

В старших классах и при изучении некоторых аспектов высшей математики можно встретить демонстрацию математической матрицы – таблицы, состоящей из элементов, расположение которых определяется при помощи порядкового номера столбца и строки. Подобные способы визуализации встречаются на уроках постоянно. Так, например, при решении задачи на нахождение роста показателей дохода за определенный период времени удобнее будет воспользоваться столбчатой диаграммой. А показать колебания акций или темпы роста температуры воздуха можно с помощью линейной диаграммы.

Помимо стандартных способов визуализации можно использовать, например комиксы, Mind-карты (ментальные карты), интерактивные презентации, дашборды или инфографику. Представление данных в простом и понятном графическом виде помогает школьникам разобраться в новом для них материале и сделать процесс обучения занимательнее и интереснее.