Сравнение аналитического и полученного конечно-разностным методом решений для круглого волокна

В последние годы по-прежнему актуальной остается проблема разработки эффективных методов анализа собственных мод оптических волноводов и волокон различных типов и конфигураций. Так в работе [1] рассматривается широко известный метод конечных разностей в применении к расчету векторных мод фотонных волноводов. Работа [2] посвящена усовершенствованному методу эффективного индекса для расчета таких модовых характеристик как эффективный индекс и дисперсия в фотонных волноводах. Продолжают активно изучаться круглые двух- и трехслойные волокна со ступенчатым профилем показателя преломления [3]. Особое внимание уделяется аналитическим и около аналитическим [4] методам анализа слабонаправляющих волокон.

В данной работе проведено численное сравнение аналитического решения и решения, полученного конечно-разностным методом, задачи расчета собственных пространственных мод оптического волокна со ступенчатым показателем преломления.

1. Конечно-разностный метод решения волновых уравнений

В работе [1] рассматривается метод конечноразностного решения векторных волновых уравнений для монохроматического света для расчета мод в оптическом волноводе. Однако расчет был проведен только для электрической составляющей электромагнитного поля. Соответствующих формул и самого расчета для магнитной составляющей светового поля в [1] нет. Поэтому в этом разделе мы приведем расчетные формулы для обеих составляющих электромагнитного поля.

Рассмотрим однородные волновые уравнения для монохроматического излучения в диэлектрической среде без источников:

v ² E + v ( v in n ² ■ E ) + k 02 n ² E = 0, (1)

V ² H - ( V x H ) xV in n ² + n ² k ₀ ² H = 0, (2) где n – показатель преломления среды, зависящий от поперечных координат (x,y) , k ₀ = 2 п / X - волно

вое число в вакууме, X - длина волны света. Далее применим уравнения (1) и (2) для волноводов, однородных вдоль продольной оси z . При этом электрическая и магнитная составляющие поля можно представить в виде E ( x , y , z ) = E ( x , y )exp( - ik z z ) и H ( x , y , z ) = H ( x , y ) exp( - ik z z ), где E ( x , y ) и H ( x , y ) – напряженности составляющих поля в поперечной плоскости, k_z – константа распространения. Далее

используются граничные условия Неймана = 0 д n

дн _     _ и ---= 0 , где n - вектор нормали к границам ис- д n

следуемой области.

Принимая во внимание инвариантность волновода вдоль продольной оси z и справедливость равенств ^{д ln n} Z = 0, ^дEZ =- ik,E и ^дHZ =- ikH , / дz    ’ / оz      ^z        / оz      ^z ’

векторные уравнения (1) и (2) можно представить в матричной форме:

P xx P yx	P xy p 1 yy J	E x E y	= k z		Ex x I E y J
Q xx	Q xy "	Г H x	1	= k		Г H x
Q yx	Q yy j	[ H y	J		z	I H y

где непрерывные дифференциальные операторы P_ij и Q_ij определяются следующим образом:

PE xxx

PE yy y

PE xy y

P yx E x

Q xx H x

д  д (1п n ² ■ E_x )

д x     д x

д ² E     2,2

+--y- + n k^Ex, дy2        0 x

д ² E y + д Г д (1п n² ■ E y ) д x ²    д y      д y

+ n ² k 02 E y ,

д Гд(1пn2 ■ Ey) 1 д2Ey дx      дy        дx дy ’

д Гд(1п n2 ■ Ex) 1 д2Ex дy      дx        дy дx ’

д ² H_x дx²

+ (1 + in n ²) ⁵2H^ - ^{v 7} д y ²

д(, 2дH)

-—I inn —x 1 + n k0H, дy (     дy J

	H	d 2 Hy
Q H = ( 1 + ln n	2)---- + ’ dx 2	d 2
sL i 5 H y' --1 In n 2 —- 6У l      d y , d QXy H y    . ^ On	] + n 2 k 0 H y n 2 ^ H- ) _ d x	,            (10) , 2 d2 hv - ln n 2------ y- ,      (11) d y d x
d Q H =— (ln, yx x   d x v	2 d H_ n 2----) — d y	In n 2 ^-H^ .     (12) d x d y

Заменяя непрерывные дифференциальные операторы конечно-разностными, получаем две независимые задачи на собственные значения относительно квадрата константы распространения:

AE = kZE ,(13)

BH = kZ H .(14)

Размерность каждой из задач (13) и (14) 2M х 2M , где M = nn,, здесь nT, n„ - количество xyx y узлов сетки по соответствующим осям. Вектор-столбцы E и H , являются собственными векторами в задачах (13) и (14) и содержат отсчеты всех четырех поперечных компонент моды.

• 2.    Аналитическое решение волновых уравнений для круглого волокна со ступенчатым профилем показателя преломления

Известны характеристические уравнения относительно константы распространения моды, для каждого типа мод, способных распространяться в круглом волокне со ступенчатым профилем показателя преломления [5].

Таблица 1. Характеристические уравнения для круглого волокна со ступенчатым профиле

HE vm — EH vm —	[ j V ( u ) + k V ( w ) |x 1 uj ; ( u ) wk ; ( w ) J XJ J M + n 2 K V ( W ) | = 1 UJ v ,( U ) n20WKv(W ) j 2 = f vk z ) f V Y L k 0 n co J l UW J
TE 0 m —	J 1 ( U ) + K 1 ( W ) UJ 0 (U ) WK 0 ( W )
TM 0 m —	n 2o J 1 ( U ) + n 2i K 1 ( W ) UJ 0 ( U ) WK 0 ( W )

Величины, входящие в выражения таблицы 1: n_co - показатель преломления сердечника;

• n_cl - показатель преломления оболочки;

• 1     2п         .

k ₀ = — , где А _о — длина волны исследуемого излу-

X о чения в мкм;

U = р ( к 0 nZ o — k Z ) ^1/2 — параметр моды в сердечнике; W = р ( k Z — к 02 nZ l ) ^1/2 — параметр (направляемой) моды в оболочке;

• V = k _о р ( n 2 _o — n cl ) — волноводный параметр;

• р — радиус сердечника в мкм;

• k_z — константа распространения моды;

J v — функция Бесселя первого рода порядка v ;

K_v — модифицированная функция Бесселя второго рода порядка v .

Также существует соотношение, связывающее параметр волокна V и параметры моды в оболочке и сердечнике W и U :

• V ² = W ² + U ² .

Выразив W через U и V и подставив вместо k Z выражение kZ = ( k ₀ n_co + U / р )( k ₀ n_co — U / р ), можно рассматривать характеристические уравнения как уравнения относительно параметра моды в сердечнике U .

Согласно введенным в [5] обозначениям, каждой моде присваивается два индекса: v — порядок моды, m — номер корня соответствующего характеристического уравнения. При этом корни нумеруются так, чтобы m = 1 соответствовал наименьшему U .

Условие отсечки U = V означает, что для направляемых мод решения характеристических уравнений следует искать только в области U <  V или, что то же самое, константы распространения направляемых мод должны лежать в интервале ^k 0 n cl <  ^kz ^ ^k 0 n co .

Таким образом, если корень уравнения определяющего отсечку соответствующей моды не принадлежит области U <  V , для волновода с таким V эта мода не существует. Гибридная мода HE _n условия отсечки не имеет и, следовательно, существует всегда. Круглый волновод со ступенчатым профилем является одномодовым, то есть в нем распространяется только HE 11 , если его волноводный параметр 0 <  V <  2,405.

Когда определена константа распространения, собственно составляющие моды рассчитываются по также известным формулам. Например, поперечные компоненты гибридных HE_vm и EH _vm мод, будут определяться следующим образом (см. таблицу 2).

Таблица 2. Формулы для расчета поперечных электрических составляющих HEvm и EHvm моды в полярных координатах

Компонента	Сердцевина	Оболочка
Er	a ! J v - 1 ( UR ) + a 2 J v + 1 ( UR ) , "          J v (U )          f v ( ф )	U axK v - 1 ( WR ) - a 2 K v + 1 ( WR ) _ . - W        K v ( W )         f v ( ф )
E ф	a 1 J v - 1( UR ) - a 2 J v + 1 ( UR )     . "          J v (U )          g v ( ф )	U a 1 K v - 1( WR ) + a 2 K v + 1 ( WR )     . - W         K v (W )         g v ( V )

Распределение основной поперечной состав-

Здесь

R = r / p - нормированный радиус, F2 — 1      F2 +1.

a 1 = —2—, a ₂ = -^2— - коэффициенты, рассчитываются через ниже следующие параметры:

( uw Y

Fi = II

• ²    ( V J b 1 + b ₂

1 J J v - 1 ( U ) J v _{+ 1}( U ) 1 2 U [ J v (U ) J v (U ) J

1 J K v - 1 ( W ) ₊ K v + 1 ( W ) |. 2 W 1 K v (W )    K v (W ) J ;

cos(vф) - четные моды(v - четное) sin(vф) - нечетные моды(v - нечетное) ’ gv (ф) =

- sin( v ф ) - четные моды(v - четное ) cos( v ф ) - нечетные моды(v - нечетное )

На границе двух сред при R = 1 оба выражения для каждой из поперечных составляющих мод в сердечнике и оболочке дают одинаковый результат. Собственно из этого условия непрерывности и вытекают характеристические уравнения.

Переходя к декартовым координатам, получаем следующие выражения:

E x = E_r cos ф - E _ф sin ф , E y = E r sin Ф - E _ф cos ф .

3 . Численные результаты

Рассматривается слабонаправляющий волновод с _ r = 3 u m            .

радиусом сердечника ^co и показателями пре- n = 1,47 n, = 1,463

ломления ^co и ^cl в сердечнике и в оболочке, соответственно. Расчет производится для

X„ = 1,3 um длины волны излучения 0   ,     . Так как вол новодный параметр для данной модели Г = 2 078 < 2 405

’    < ’    , то волокно является одномодо- вым. Результаты расчета константы распростране- kz

n

ния и эффективного индекса

= — eff k HE 0 моды 11 , конечно-разностным и аналитическим методами показаны в таблице 3.

ляющей моды HE ₁₁ – E_y , показаны на рис. 1.

Таблица 3. Значения параметров моды HE ₁₁ для слабонаправляющего волокна, описанного в тексте, рассчитанных разными методами

Параметр	Конечно-разностный метод, n x х n y = 52 х 52	Аналитическое решение
k z , u m ^1	7,0855	7,0859
n eff	1,4660	1,4661

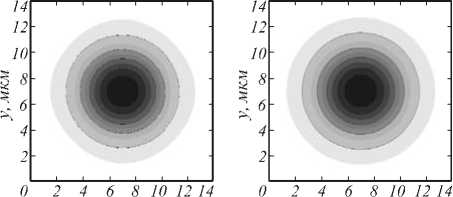
а)                               б)

Рис. 1. Графики распределения компоненты E_y моды HE ₁₁ для слабонаправляющего волокна, описанного в тексте, (а) – конечно-разностный метод n x х n y = 52 х 52 , (б) - аналитическое решение

Среднеквадратическое отклонение между двумя решениями для E_y , нормированными по интенсивности на единицу, по области W x х W y = 14 u m х 14 u m составило 0,00444 .

Далее рассматривается круглое волокно со ступенчатым профилем показателя преломления n_co = 1,5 - в сердечнике и n_cl = 1 - в оболочке, с радиусом сердечника r_co = 0,52 u m . Длина волны излучения в вакууме принимается равной Х ₀ = 1,55 u m . Это волокно также является одномодовым, так как его волноводный параметр V = 2,357 <  2,405. Распределение основной поперечной составляющей моды HE ₁₁ – E_y , показаны на рис. 2.

Из рис. 2 видно, что, не смотря на круглое сечение сердечника и квадратное сечение оболочки волокна, преимущественная по величине составляющая элек- трического поля Ey имеет эллиптическую форму. В диапазоне изменения числа узлов сетки по каждой из осей координат от 30 до 68 конечно-разностный метод не демонстрирует равномерной сходимости рассчитываемого эффективного индекса HE11 круглого волокна к аналитическому решению (рис. 3).

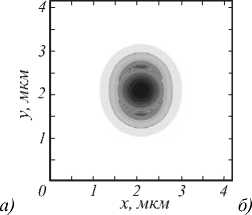
Рис. 2. Графики распределения компоненты E_y

моды HE ₁₁ для круглого волокна, описанного в тексте, (а) - конечно-разностный метод n x х n y = 52 х 52 , (б) – аналитическое решение

1,265

1,260

1,255

1,250

1,245

1,240

1,235

1,230

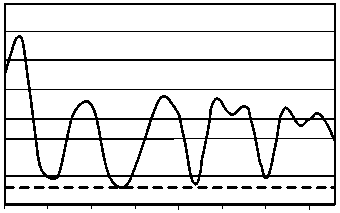
30 35 40 45 50 55 60 65

Рис. 3. График зависимости значения эффективного индекса n_eff направляемой моды HE ₁₁ круглого волокна, описанного в тексте от числа узлов сетки по каждой из осей в метода конечных разностей; штриховой линией показано точное значение, полученное аналитическим методом

Из рис. 3 видно, что максимальное относительное отклонение рассчитанного neff от точного значения nefr = 1,2333 при nx, ny > 35 составляет около 1,1%.

Заключение

Таким образом, в работе подробно рассмотрен конечно-разностный подход к решению волновых уравнений. Получены матричные уравнения относительно константы распространения моды отдельно для поперечных электрических и магнитных составляющих моды, отсчеты которых получаются в данном случае как собственные векторы матриц. Проведен расчет основной моды круглых одномодовых волокон методом конечных разностей, и показано, что результирующие константы распространения и распределения полей хорошо согласуются с результатами, полученными аналитически (отклонение около 1%).

Работа выполнена при поддержке Министерства образования и науки РФ, правительства Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), а также при поддержке гранта Президента РФ № НШ-1007.2003.01 и гранта РФФИ №05-08-50298.