Сравнение архитектур нейронных сетей для подавления мультипликативного шума на изображениях

Радиолокатор с синтезированной апертурой (РСА) обладает множеством преимуществ по сравнению с оптическим дистанционным зондированием [1]. РСА позволяет получать изображения круглосуточно, в любую погоду, на значительном расстоянии от носителя и в широкой полосе обзора. РСА-оборудование может быть размещено на спутниках, летательных, а в случае гидролокации и на подводных аппаратах. В связи с этим изображения, полученные с помощью РСА, используются во многих областях, таких как картографирование местности, получение данных в интересах лесного и сельского хозяйства, при мониторинге труднодоступных областей и т.п.

Основным недостатком изображений, полученных с помощью РСА, является наличие мультипликативного спекл-шума, который ухудшает качество изображений и снижает эффективность различных автоматизированных методов извлечения информации, включая нейросетевые. Для обработки изображений РСА с целью классификации, сегментации и обнаружения желательно уменьшение уровня спекл-шума. Аналогичные проблемы встречаются при анализе данных гидролокаторов с синтезированной апертурой и ультразвуковых медицинских изображений.

В настоящее время обучение нейронных сетей (НС) для обработки РЛИ часто производится на специально зашумленных оптических изображениях. В этом случае НС вынуждена сочетать в себе функции шумоподавления и обнаружения/классификации. Однако эти функции можно и разделить между двумя НС: шумоподавителем и обнаружителем. Плюсами такого подхода являются возможность оптимизации шумоподавления, использования для обнаруже-ния/классификации объектов, существующих НС, уже обученных на оптических изображениях, и получение в процессе обработки изображения с уменьшенными шумами, доступного для просмотра и анализа человеком-оператором.

Цель работы заключается в разработке способа фильтрации шумов на изображении с помощью НС малой вычислительной сложности, не требующей большого количества обучающего материала.

Обзор методов фильтрации спекл-шума

Методы фильтрации спекл-шума в общем случае можно разделить на четыре основные категории:

• •    методы пространственной области [2 ‒ 7],

• •    вейвлет-методы [8 ‒ 11],

• •    нелокальные методы [12, 13],

• •    нейросетевые методы [14 ‒ 19].

К методам, работающим в пространственной области, относятся медианный фильтр [2], фильтр Ли [3], фильтр Фроста [4], фильтр Куана [5], фильтр Перона и Малика [6], билатеральный фильтр [7].

Методы на основе вейвлетов более эффективны, чем методы пространственной области. Они позволяют выполнять анализ изображения в нескольких разрешениях и при нестационарных характеристиках. Данные методы фильтруют изображения в области преобразований, оценивая обесшумленные коэффициенты, а затем применяют обратное преобразование для получения очищенного изображения. В работах [8 ‒ 11] применяется логарифмирование данных для преобразования мультипликативного шума в аддитивный.

В то время как локальные методы используют информацию из окон ограниченного размера, нелокальные методы пытаются дополнительно использовать информацию обо всем изображении. В [12] представлен фильтр нелокального среднего (non-local mean, NLM), который вычисляет взвешенное среднее значение всех пикселей изображения, а веса зависят от их сходства с целевым пикселем. Весовые коэффициенты определяются путем вычисления евклидова расстояния между окружающим участком с центром в соседнем пикселе и локальным участком с центром в целевом пикселе. В работе [13] для адаптации нелокального метода был предложен вероятностный алгоритм на основе фрагментов. Авторы разработали меру сходства фрагментов, которая обобщается на случай мультипликативного, негауссового спекл-шума.

В последние годы в области фильтрации спекл-шума на радиолокационных изображениях (РЛИ) стали активно применяться методы глубокого обучения, в частности глубокие нейронные сети. В [14] представлен SAR-CNN, который применяет схожую с DnCNN [15] методику фильтрации спекл-шума и использует гомоморфный подход для работы с мультипликативной моделью шума и новую меру сходства для распределения спекл-шума в качестве функции потерь, а не обычное евклидово расстояние. Чистые данные для обучения получаются путем усреднения разновременных изображений SAR. В [16] предложена остаточная свёрточная сеть (ID-CNN), обученная на синтетических РЛИ, для прямой оценки шума в исходной области. Удаление спекл-шума на изображении получается путем деления зашумленного изображения на оцененный шум. В [17] для удаления спекл-шума предложен метод IDGAN, основанный на генеративной состязательной сети и обученный с использованием взвешенной комбинации евклидовых потерь, перцептивной потери и состязательной потери. В [18] для увеличения поля восприимчивости и улучшения распространения и повторного использования признаков была предложена расширенная сеть с плотными связями (SAR-DDCN), обученная с использованием евклидова расстояния. В [19] была предложена комбинация гибридных расширенных сверток и модулей пространственного и канального внимания с помощью остаточной архитектуры, названной HDRANet, для дальнейшего улучшения возможности извлечения признаков. В [20] предложено одновременное использование нейронной сети на базе свёрточной архитектуры для увеличения поля восприимчивости с применением механизма автокодировщика для извлечения важных признаков.

Описание архитектуры

Предлагаемый метод базируется на совмещении традиционных и нейросетевых (НС) подходов к фильтрации изображений. Как и в традиционном подходе, обработка ведется в окне небольшого размера. Однако предсказание центрального пикселя окна производится с помощью специально обученной НС.

Ключевым отличием предлагаемого метода является замена НС, работающей с изображением в целом, на НС, последовательно работающую с участками изображения (окнами). При этом обеспечивается просмотр сетью большего количества локальных особенностей изображения, что обеспечивает большую эффективность обучения при том же наборе данных.

Модель полносвязной НС (ПСНС) представлена на рис. 1. Она состоит из блоков, которые содержат полносвязный слой, пакетную нормализацию и функцию активации ReLU. Размер выходного слоя зависит от типа решаемой задачи: классификация или регрессия. Количество нейронов в скрытых слоях равно размеру входа, который, в свою очередь, кратен n × n , где n – размер скользящего окна.

Зашумленные данные 1ХМ

Полносвязный слой

Пакетная нормализация

ReLU

Полносвязный слой

Пакетная нормализация

ТО:

ReLU

Выходной слой

Пиксель

Рис. 1. Архитектура полносвязного НС-фильтра

В связи с небольшой размерностью такой НС процесс ее обучения вычислительно не сложен и возможен даже без применения аппаратного ускорения на графических процессорах. А малый размер окна приводит к тому, что даже единственное изображение достаточно большого размера содержит в себе большой объем обучающих данных (возможно использование как перекрывающихся, так и неперекрываю-щихся окон).

В табл. 1 представлена структура ПСНС.

Пример формирования обучающих данных представлен на рис. 2.

а)

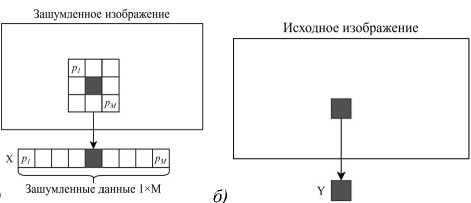
Рис. 2. Пример формирования обучающих данных

Табл. 1. Структура нейросетевого фильтра

Параметры	Описание
Количество слоёв	N слоёв: •    1 входной слой •    N ‒2 скрытых слоя •    1 выходной слой
Структура входного слоя	•    Полносвязный слой (количество входов w × h ( w ‒ ширина скользящего окна, h ‒ высота)) •    пакетная нормализация •    функция активации ReLU
Структура скрытого слоя	•    Полносвязный слой (количество нейронов совпадает с размером входного слоя) пакетная нормализация •    функция активации ReLU
Структура выходного слоя	Полносвязный слой: •    1 нейрон для задачи регрессии •    256 нейронов для задачи классификации

Результаты и обсуждение

Для формирования обучающего и тестового набора необходимо иметь исходные (незашумленные) изображения, изображения с шумом, изображения после обработки фильтрами. В связи с этим необходимо создать синтетические аналоги РЛИ искус- ственным образом, накладывая на оптические изображения спекл-шум согласно формуле [22]:

I ‘ ( x , y ) = I ( x , y ) ( 1 + n ( x , y ) ) , ⁽¹⁾

где I ( x, y ) – исходное изображение (неискаженное); n ( x, y ) – случайный процесс, описывающий спекл-шум.

Для обучения НС-фильтра желательно, чтобы оптическая обучающая выборка примерно соответствовала характеристикам планируемых к обработке изображений (лес, горы, город, море). Если в данный момент недоступны изображения конкретного участка местности, то можно использовать похожие. Поскольку в настоящий момент доступно большое количество оптических изображений различных участков земной поверхности, то такой выбор не должен составлять большой проблемы.

В работе [21] показано, что распределение шума на РЛИ соответствует распределению Рэлея с параметром масштаба 0,27.

На рис. 3 а, б представлены примеры исходных оптических изображений, на рис. 3 в, г представлены примеры зашумленных изображений, на которых обучались и тестировались фильтры.

в)

Рис. 3. Примеры оптических изображений

г)

Архитектура фильтра на основе свёрточной нейронной сети (СНС) представлена на рис. 4.

В табл. 2 представлена структура фильтра на основе СНС.

Обучение нейросетевых подходов выполнялось на графическом ускорителе RTX 2080 TI. Параметры обучения ПСНС представлены в табл. 3.

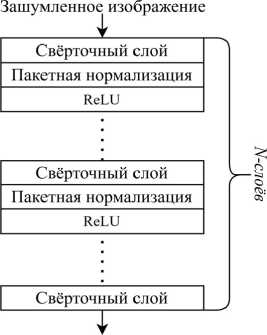
Очищенное изображение

Рис. 4. Архитектура фильтра на основе СНС

Табл. 2. Структура фильтра на основе СНС

Параметры	Описание
Количество слоёв	N слоёв: •    1 входной слой •    N ‒2 скрытых слоя •    1 выходной слой
Структура входного слоя	•    Свёрточный слой (64 фильтра, размер фильтра – 3×3) •    пакетная нормализация •    функция активации ReLU
Структура скрытого слоя	•    Свёрточный слой (64 фильтра, размер фильтра – 3×3) •    пакетная нормализация •    функция активации ReLU
Структура выходного слоя	Свёрточный слой (64 фильтра, размер фильтра – 3×3)

Параметры обучения СНС представлены в табл. 4.

В табл. 5 представлены результаты сравнения СНС, ПСНС и фильтров с оптимальными параметрами, взятыми из работы [21] с помощью метрик SSIM [23] и GMSD [24]. Сравниваются исходные незашумлен-ные оптические изображения и изображения после фильтрации. Размер тестовой выборки – 128 изображений, разрешение – 512×512.

Табл. 3. Параметры обучения ПСНС

Параметр	Тип задачи
	Классификация     Регрессия
Кол-во эпох	30
Размер батча	32768 векторов
Скорость обучения	10-3
Размер выборки	5274752 векторов (128 изображений (шаг 3))
Размер обучающей выборки	4219800
Размер валидационной выборки	1054952
Функция потерь	Перекрёстная энтропия	Среднеквадратическая ошибка
Метод обучения	Adam

Табл. 4. Параметры обучения СНС

Параметр	Значение
Кол-во эпох	100
Размер батча	4 (для N =20)
Скорость обучения	10 –3
Размер обучающей выборки	1024
Размер валидационной выборки	128
Функция потерь	Среднеквадратическая ошибка
Метод обучения	Adam

Табл. 5. Результаты сравнения СНС, ПСНС и фильтров

Метод	SSIM	GMSD
ПСНС ( N = 10, 11×11), классификация	0,871	0,063
ПСНС ( N =20, 11×11), классификация	0,872	0,065
ПСНС ( N =10, 11×11), регрессия	0 , 873	0 , 065
ПСНС ( N =20, 11×11), регрессия	0,866	0,065
СНС ( N = 10)	0,890	0,057
СНС ( N =20)	0,895	0,056
DnCNN Matlab	0.834	0,067
Билатеральный фильтр	0,818	0,084
Фильтр Перона и Малика (Quad)	0,807	0,079
Фильтр Ли	0,796	0,084
Фильтр Фроста	0,787	0,112
Медианный фильтр	0,747	0,109
Фильтр Куана	0,636	0,112

На рис. 5 а, б представлены результаты фильтрации изображений 3 а, б с помощью ПСНС ( N = 10, 11×11, регрессия). На рис. 5 в, г представлены результаты фильтрации изображений 3 а, б с помощью СНС ( N =20).

На рис. 6 а представлены срезы для рис. 3 а, в и 5 а, в. По оси абсцисс отложены индексы пикселей, а по оси ординат – нормированная интенсивность. Отметим, что для того чтобы графики не пересекались, они были сдвинуты вдоль оси ординат . На рис. 6 б белой линией показано положение среза.

а)

б)

в)

Рис. 5. Результаты фильтрации: а,б) ПСНС (N = 10, 11×11, регрессия), в,г) результаты фильтрации СНС (N = 20)

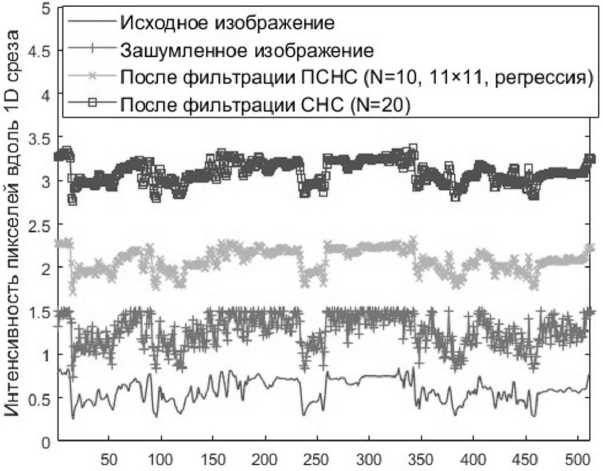
Индексы пикселей вдоль 1D среза

а)

Рис. 6. Срезы исходного, зашумленного и отфильтрованных изображений

Видно, что НС-фильтры хорошо подавляют шум, сохраняя при этом особенности исходного изображения (границы и малоразмерные объекты). Это соответствует высоким значениям метрики SSIM и малым значениях GMSD. Комбинация этих метрик, как по- казала практика, хорошо отражает качество фильтрации, оцениваемое экспертом визуально.

На рис. 7 а представлено исходное зашумленное РЛИ (разрешение 512×512) [26], на рис. 7 б представлен результат фильтрации ПСНС ( N = 10,

11×11, регрессия), на рис. 7 в – результат фильтрации СНС ( N = 20)

а)

б)

в)

Рис. 7. а) Пример РЛИ; результаты фильтрации: б) ПСНС (N = 10, 11×11, регрессия), в) результаты фильтрации СНС (N = 20)

На рис. 8 а – в представлены фрагменты рис. 7 а – в.

На рис. 9а представлены срезы рис. 8а – в. По оси абсцисс отложены индексы пикселей, а по оси ординат – нормированная интенсивность . Чтобы графики не пересекались, они были сдвинуты вдоль оси ординат.

На рис. 9 б белой линией показано положение среза.

в)

б)

Рис. 8. а) Фрагмент рис. 7а; б) фрагмент рис. 7б, в) фрагмент рис. 7в

В табл. 6 представлено сравнение ПСНС ( N =10, 11×11, регрессия) и СНС ( N = 20), обученных на ограниченном наборе данных (16 изображений). Сравнение выполнялось в двух режимах: на CPU (Intel Core i7-8700K, 3.7 ГГц) и GPU (RTX 2080 TI).

Табл. 6. Результаты сравнения СНС, ПСНС

Параметр	СНС	ПСНС, регрессия
Кол-во эпох	100	15
Время обучения на CPU, с	1800	600
Время обучения на GPU, с	148	202
Ср. время обработки изображения (512×512) на CPU, с	0,6	0,4
Ср. время обработки изображения (512×512) на GPU, с	0,001	0,002
Кол-во изображений для обучения	16
Кол-во изображений для тестирования	128
SSIM	0,81	0,852
GMSD	0,088	0,070

а)

б)

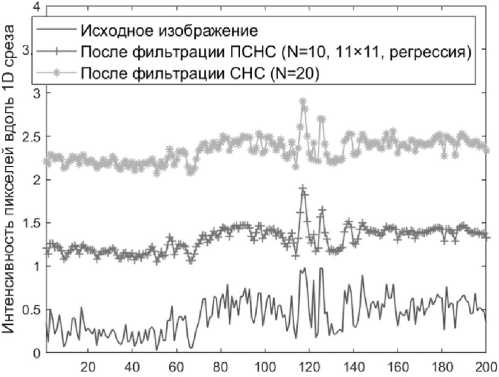
Индексы пикселей вдоль 1D среза

Рис. 9. Срезы зашумленного и отфильтрованных изображений

Результаты экспериментов показали, что нейросетевые подходы превосходят по качеству фильтрации традиционные, при этом подход на основе ПСНС обеспечивает высокое качестве фильтрации при уменьшенном объёме обучающего материала.

Заключение

Описанная методика фильтрации на основе НС позволяет фильтровать шумы на изображениях, которые могут содержать как однородные области, так и малоразмерные объекты, и резкие границы. Рассмот- рено применение наиболее распространенных в настоящее время стандартных сверточных НС и полносвязных НС небольшой размерности, работающих с небольшими участками изображения (окнами) и предсказывающими только центральный пиксель окна. В последнем случае обработка изображения произвольного размера осуществляется последовательным перемещением скользящего окна по изображению.

Проведенное сравнение ПСНС, СНС и классических фильтров показывает, что нейросетевые подходы превосходят по качеству фильтрации традиционные . Однако существенным недостатком нейросетевых подходов является необходимость использования большого количества обучающего материала. Предложенные архитектуры на основе ПСНС обеспечивают высокое качество фильтрации при существенно уменьшенном объёме обучающего материала по сравнению с СНС, что является их важным преимуществом .

Планируется исследование применения предложенной архитектуры к фильтрации других видов шумов.

Исследования выполнены при финансовой поддержке Минобрнауки России в рамках соглашения о предоставлении гранта в форме субсидий из федерального бюджета на осуществление государственной поддержки создания и развития научных центров мирового уровня, выполняющих исследования и разработки по приоритетам научно-технологического развития от 20 апреля 2022 года №075-15-2022-311.