Сравнение авторегрессионной и нечеткой модели прогнозирования котировок цен на нефть
Бесплатный доступ
В данной статье рассматривается такая проблема, как прогнозирование цен на нефть. Данная тема весьма актуальна в наше время, ведь «черное золото» играет огромную роль в экономике всего мира. В процессе построены модели прогнозирования цен на нефть в MS Excel и среде fuzzyTECH. Представлены результаты, сделаны выводы, а также даны рекомендации по улучшению моделей.
Прогнозирование, нейронные сети, авторегрессионная модель
Короткий адрес: https://sciup.org/140278406
IDR: 140278406
Текст научной статьи Сравнение авторегрессионной и нечеткой модели прогнозирования котировок цен на нефть
Проблема прогнозирования цены на нефть была и остается актуальной, в той или иной степени, практически для всех стран мира. Согласно оценкам большинства ведущих мировых экспертов и аналитических агентств, минеральное органическое топливо (в частности, нефть) по-прежнему остается доминантой в мировой энергетике и стратегическим ресурсом для многих государств. Неустойчивость цен на нефть слишком дорого обходится странам, мировой экономике, политическим системам, населению.
Для России уровень актуальности проблемы прогнозирования цены на нефть особенно высок. Этому есть ряд причин:
-
- Россия является одним из лидеров мировой энергетики и крупнейшим участником международных энергетических рынков,
-
- Россия является одним из крупнейших экспортеров сырой нефти и природного газа,
-
- ситуация на мировом рынке нефтяных цен во многом определяет ситуацию с ценой бензина на внутреннем рынке РФ,
-
- цены на нефть являются базой для формирования цен на другие энергоносители и ресурсы,
-
- цены на нефть влияют на стоимость акций нефтяных компаний и на инвестиции,
-
- исторически цена на нефть определяет текущее состояние отечественной экономики и ее перспективы.
Таким образом, без грамотного прогнозирования цены на нефть невозможны разработка и реализация мероприятий, направленных на стабилизацию российской экономики в современных условиях и создание условий для ее устойчивого развития.
В настоящее время успех в бизнесе зависит от правильно принятых решений, хорошо обдуманных шагов и четко выраженной поставленной цели. В условиях рыночной не стационарности ценность приобретают методы, способные прогнозировать цены на рынке, прибыль или убытки, получаемые в реальном процессе торговли, с учетом спрэда, комиссии, проскальзывания и времени совершения сделки.
Существуют огромное количество эконометрических методов, которые используются для прогнозирования цен на нефть, но мы остановимся лишь на авторегрессионной модели первого порядка.
Прогнозирование с использованием модели авторегрессии опирается на предыдущие значения продаж. Слово авторегрессия означает зависимость последующего значения продажи от предыдущих продаж. Зависимость в случае авторегрессии предполагается линейная, то есть прогноз представляет собой сумму продаж за предыдущие дни с некоторыми коэффициентами, которые являются постоянными и определяют параметры модели авторегрессии. В случае моделей авторегрессии, цены предсказываются исходя из прошлой динамики.
Авторегрессионная модель первого порядка имеет следующую формулу:
Y i = a o + а*уи+Е 1
Как видно из формулы выше, линейная модель авторегрессии первого порядка состоит только из одного влияющего фактора, а именно из y-1, то есть изучается наиболее тесная зависимость только от того каким был итоговый показатель периодом с шагом назад.
В качестве программного средства был выбран Microsoft Excel. Для того что бы сделать прогноз на основе этой модели воспользуемся пакетом "Анализ данных" в MS Excel.
Составим прогноз цены на нефть на следующие 3 дня вперед. Для этого нужно найти авторегрессию ценового ряда, то есть тесноту связи между соседними членами ценового ряда (рисунок 1).
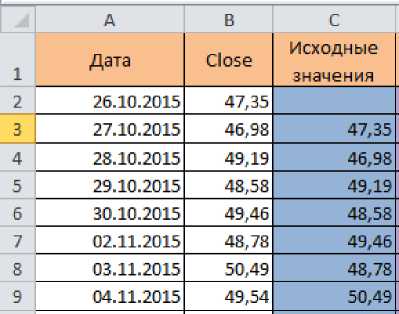
Рисунок 1 Котировки цен на нефть. Сдвиг временного ряда
Далее рассчитаем коэффициенты авторегрессии для ценового ряда нефти. Для расчетов коэффициентов воспользуемся надстройкой «Анализ данных» и разделом «Регрессия». После ввода параметров выйдет отчет по регрессии (рисунок 2).
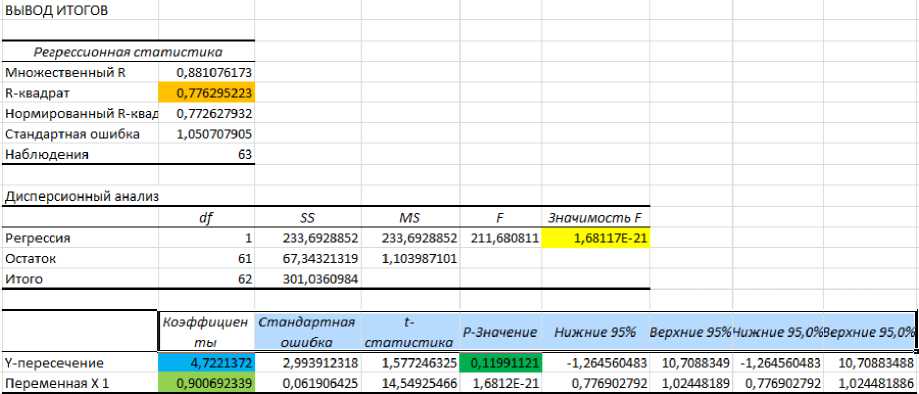
Рисунок 2 Отчет по регрессии
Коэффициент R– квадрат показывает качество модели, чем выше это значение, тем лучше. Значимость F = 0 –это говорит о хорошем качестве всего уравнения.
Модель динамики цены на нефть описывается следующим уравнением: Y=4,72214 + 0, 90069*yt-1
Авторегрессия будет строиться до последней строчки, пока есть значения курса цен на нефть. Далее необходимо прогнозировать уже от предыдущего прогноза, поэтому в следующей ячейке введем формулу, берущую значения предыдущего прогноза.
Далее после полученных значений, считаем значение нашего прогноза (рисунок 3).
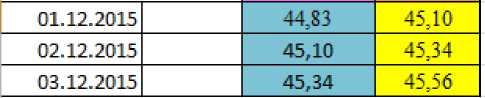
Рисунок 3 Значение прогноза
На основе авторегрессии, построим график прогнозных значений (рисунок 4).
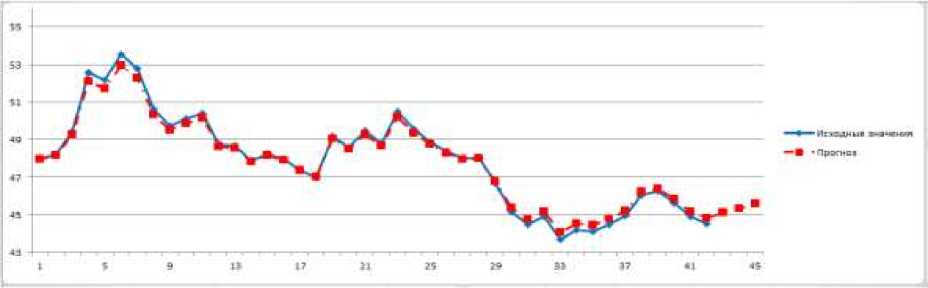
Рисунок 4 График прогнозных значений
На графике мы видим, что прогноз очень близок к реальным данным. Среднее значение погрешности равно 0,19. Использование регрессионных моделей позволяет построить довольно четкие прогнозные модели.
В отличие от традиционной математики, требующей на каждом шаге моделирования точных и однозначных формулировок закономерностей, нечеткая логика предлагает совершенно иной уровень мышления, благодаря которому творческий процесс моделирования происходит на наивысшем уровне абстракции, при котором постулируется лишь минимальный набор закономерностей [ Ошибка! Источник ссылки не найден. ].
В качестве программного средства был выбран fuzzyTECH - этот пакет программ является средством моделирования и оптимизации проектов создания нечетких систем управления на базе микроконтроллеров.
Теперь спрогнозируем аналогичные данные в среде fuzzyTECH (рисунок 5).
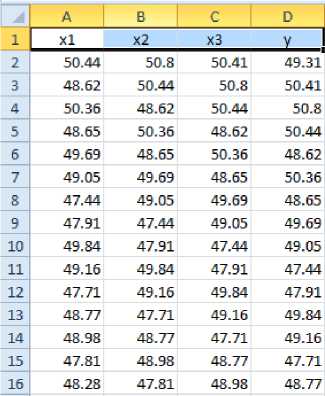
Рисунок 5 Исходные данные
Далее, сохраним эту обучающую выборку в файл с расширением csv.
Модель будет содержать три входных переменных и одну выходную. Первая входная переменная будет соответствовать курсу нефти на текущий банковский день, вторая — курсу нефти на предыдущий банковский день, т.е. На день (i - 1), где через i обозначен текущий банковский день. Тогда третья входная переменная будет соответствовать курсу нефти на (i - 2) банковский день. Указываем по 3 функции принадлежности для каждой входной переменной и 5 для выходной. Необходимо более точно специфицировать термы и их функции принадлежности для входных и выходной лингвистических переменных разрабатываемой системы нечеткого вывода. Для каждой переменной определяем область определения (43;54), для более точного моделирования (рисунок 6).
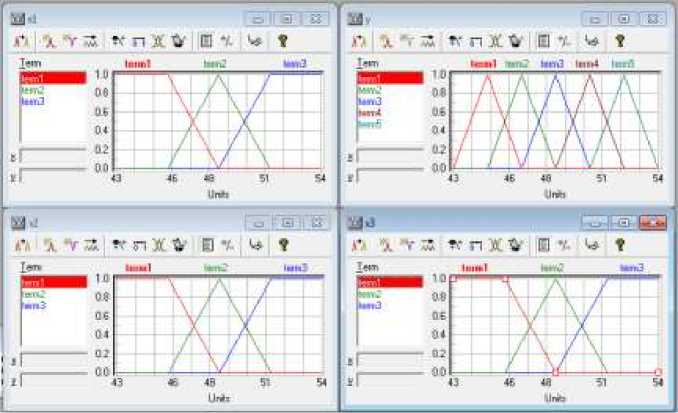
Рисунок 6 Редактируем переменные
После окончания работы с мастером нечеткого проекта будет создан прототип системы нечеткого вывода. Структура системы нечеткого вывода с измененными значениями текстовых блоков (рисунок 7):
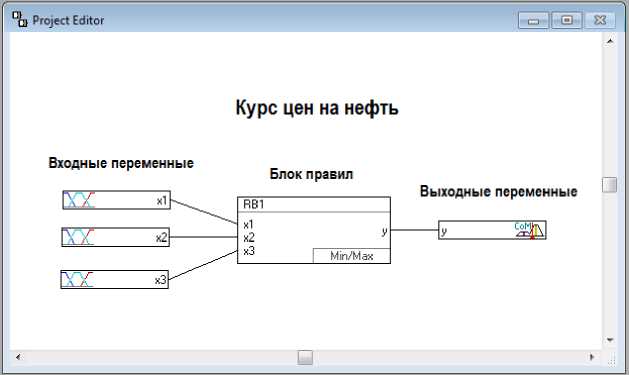
Рисунок 7 Прототип системы нечеткого вывода
Определим базу правил. Первоначально база правил нечеткого вывода пуста, для их определения следует использовать воспользоваться пунктом контекстного меню Spreadsheet Full Editor, после выбора, которого будет сгенерирована база из 135 правил.
Теперь необходимо обучить нечеткую систему, используя обучающую выборку (рисунок 8).
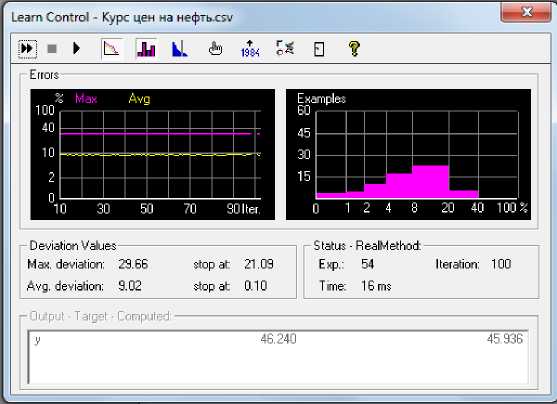
Рисунок 8 Обучение сети
Как можно видеть по рисунку максимальное отклонение от выборки при обучении составляет 29,66%, а среднее 9,02%.
Теперь проверим точность построенной системы. Предположим, что нам нужно узнать курс на 14 октября и 24 ноября (рисунок 9).
$5 Watch: Interactive Debug Mode И! ® Й ^ ^ ^ |44.9300
|
nputs: |
Outputs: |
|
|
k1 44.1100 «2 44.4800 |
у 45.8826 |
|
|
« 44.9300 |
||

^ Watch: Interactive Debug Mode
|
И! ^ S |
= *1 © DEF DDE 8 |
50.6300 |
|
Inputs: |
Outputs: |
|
|
53.5300 |
V 49.8568 |
|
|
«2 |
52.7800 |
|
Рисунок 9 Проверка точности системы
Таким образом, система выдает значение курсовой стоимости, равное 45,8826 на 14 октября и 49,8568. Зная известные нам значение, погрешность равна 0,1368 в первом случае и 0,1674 во втором. Возможно, такая высокая погрешность является результатом малого количества входных переменных.
Среда fuzzyTECH предлагает нам большой выбор анализа модели. В интерактивном режиме возможно отображение поверхностей отклика системы нечёткого вывода. На них отображаются прямыми значения входных переменных, а точка пересечения прямой параллельной оси выходной переменной с поверхностью отклика, есть её значение (рисунок 10).
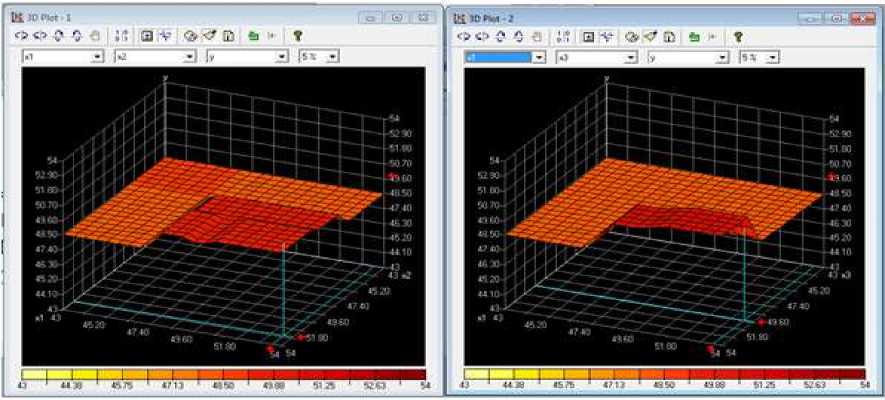
Рисунок 10 Анализ в графическом окне просмотра трехмерной поверхности нечеткого вывода
Текущие значения входных лингвистических переменных визуализируются с помощью красных стрелок на координатных осях графика поверхности.
Для окончательного анализа разработанной нечеткой модели можно воспользоваться графическим окном просмотра поверхности нечеткого вывода на плоскости (рисунок 11).
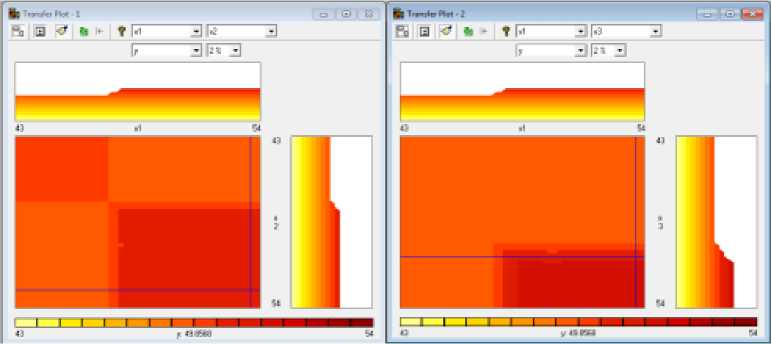
Рисунок 11 Поверхность нечеткого вывода на плоскости
Подведем итоги: среднее значение погрешности в Excel равно 0,19, в среде fuzzyTECH погрешность равна 0,15. Неточности системы построенной в excel не намного больше чем в среде fuzzyTECH.
Обе системы не идеальны. Ошибки, которые были получены, могут быть обоснованы следующими факторами: без глубоких экономических исследований невозможно определить все параметры коррелирующие с курсом цены на нефть. В данном случае мы использовали только значения курса нефти в качестве входных переменных, но есть множество экономических и политических факторов, которые влияют на цену.
Список литературы Сравнение авторегрессионной и нечеткой модели прогнозирования котировок цен на нефть
- Архипенко А.Д. Некоторые аспекты проблем прогнозирования цены на нефть на мировом рынке в современных условиях// Материалы международной конференции студентов, аспирантов и молодых ученых «Проспект свободный - 2015». 2015. С. 4-7.
- Леоненков А.В. Нечеткое моделирование в среде Matlab и fuzzytech// - СПБ.: БХВ-Петербург, 2005. - 736 c.
- Авторегрессия - моделирование и прогнозирование в Excel. [Электронный ресурс] URL: http://archie-goodwin.net/load/specializirovannye_blogi/ms_office/avtoregressija_modelirovanie_i_prognozirovanie_v_excel/28-1-0-422
- Построение прогнозных моделей курса акций с помощью авторегрессии. [Электронный ресурс] URL: http://www.economic-s.ru/index.php/practice/ryinok-tsennyih-bumag/prognozirovanie-kursa-aktsiy-s-pomoshhyu-metoda-avtoregressii-ar


