Сравнение бинарных дескрипторов особых точек изображений в условиях искажений

Выделение признаков объектов в цифровых изображениях является одной из основных задач компьютерного зрения и теории распознавания образов. Одним из видов первичных геометрических признаков объектов в цифровом изображении являются особые точки ( feature points ). В качестве таких особых точек выступают хорошо различимые локальные области изображения: края, углы, используемые в дальнейших этапах распознавания образов. Сопоставляя особые точки между собой, в ряде изображений можно решать задачи трекинга объектов, стабилизации видео, генерации панорам, трёхмерной реконструкции объектов, в системах дополненной реальности и прочее.

Особыми называются такие точки изображения, локальные окрестности которых обладают некоторыми отличительными особенностями в сравнении с окрестностями остальных точек изображения. Эти области являются отправной точкой для многих алгоритмов компьютерного зрения и подразделяются на края, углы, «блобы», рёбра. Изучение особых точек цифровых изображений восходит к концу 80-х годов XX века, когда были найдены способы их обнаружения: детекторы углов (C. Harris, M. Stephens [1], 1988; J. Shi, C. Tomasi [2], 1994; S.M. Smith и J.M. Brady (SUSAN) [3], 1997), детекторы блобов (Т. Lindeberg [4], 1998 – LoG, DoG, DoH), детектор ребра (R. Haralick [5], 1983).

Работа с особыми точками изображений основывается на следующей схеме:

• 1.    Обнаружение особой точки ( feature detection ).

• 2.    Описание особой точки через дескриптор ( feature description ).

• 3.    Сопоставление особых точек пары изображений путём сравнения их дескрипторов ( feature matching ).

Задачи сопоставления особых точек в ряде изображений в основном замыкаются на проблему определения их уникальных характеристик (дескрипторов или идентификаторов). Для обеспечения надежного соот- ветствия важно, чтобы особые точки, выделенные в изображении, обнаруживались даже при изменении масштаба и вращения изображения, при наличии шума и изменении освещения. То есть дескрипторы должны быть инвариантны к такого рода искажениям.

В Российской Федерации исследования в данном направлении проводятся в лаборатории математических методов обработки изображений Института систем обработки изображений РАН, г. Самара (В.В. Мясников [6, 7]), лаборатории компьютерной графики и мультимедиа ФВМК МГУ имени М.В. Ломоносова, г. Москва (А.С. Конушин). В Республике Беларусь исследования проводятся в ОИПИ НАН РБ в лаборатории обработки и распознавания изображений (В.В. Старовойтов) [8]. Также исследования проводятся в крупных научных центрах стран дальнего зарубежья – Швеция (Королевский технологический университет, г. Стокгольм, T. Lindeberg), Англия (Оксфордский университет, г. Оксфорд, Mark S. Nixon), Япония (Осакский университет, г. Осака, H. Liu, H. Motoda) и др.

Существуют известные дескрипторные методы сопоставления особых точек, инвариантные к различным преобразованиям, такие как SIFT: Scale-invariant feature transform (David Lowe, 1999) [9], SURF: Speeded up robust features (Herbert Bay, Andreas Ess, Tinne Tuytelaars, Luc Van Gool, 2008) [10], HOG: Histogram of oriented gradients (William T. Freeman, Michal Roth, 1994) [11], запатентованные в США.

При поиске особых точек зачастую используются низкоуровневые алгоритмы попиксельной обработки изображений. При этом алгоритмы достаточно сложны: изображения предварительно сглаживаются, вычисляются масштабные и аффинные преобразования, используются аппроксимации дифференциальных операторов. В итоге методы и алгоритмы SURF, SIFT, HOG требуют больших вычислительных ресурсов и, как следствие, имеют ограничения по времени выполнения, или обрабатываются только части нужного изображения. Поэтому перспективным направлением является получение быстрых алгоритмов обнаружения и сопоставления особенных точек изображений. Известны быстрые алгоритмы, являющиеся предметом анализа в данной статье: BRIEF, ORB, BRISK, FREAK, AKAZE, LATCH, использующие бинарные дескрипторы. Разработкой быстрых алгоритмов расчёта признаков изображений занимаются известные авторы [12, 13]: M. Calonder, G. Lowe, E. Rosten и др. Сравнительные исследования дескрипторов проводились авторами и ранее, например, в работах [14–18]. В отличие от приведённых сравнений, в нашей работе рассматривается бóльшее количество дескрипторов, активно используемых сейчас при разработке программного обеспечения.

Основной современной тенденцией является переход от расчёта аффинно-инвариантных дескрипторов локальных особенностей и их сравнения между собой к методам быстрой классификации и распознавания особых точек с обучением. Эффективность данного подхода подтверждена многими работами, приведёнными далее.

1.    Бинарные дескрипторы

В методах SIFT и SURF для расчёта дескрипторов строятся гистограммы градиентов областей вокруг особой точки. Даже несмотря на то, что метод SURF использует интегральные изображения, эти вычисления достаточно длительны.

Идея бинарных дескрипторов состоит в том, чтобы описать область вокруг особой точки двоичной строкой, полученной путём попарного сравнения яркости пикселей в заданной области. Результат сравнения будет равен «1», если яркость меньше, и «0», если яркость больше либо равна. По сути, бинарный дескриптор – это способ описать, в каком направлении убывает яркость в области особой точки.

Cравнение дескрипторов между собой будет заключаться в сравнении бит в строках. В частности, для сравнения дескрипторов в ранних методах применялись такие меры, как сумма разностей по модулю - SAD = S | f a - f b | или сумма квадратов разностей d SSD = S ( f a - f b )². В случае бинарных дескрипторов возможно использование меры Хэмминга - HAM = S XOR( f a , f b ), которая вычисляется быстро -одной командой.

К быстрым дескрипторам особых точек относят следующие: BRIEF ( Binary Robust Independent Elementary Features ) – M. Calonder, V. Lepetit, C. Strecha, P. Fua [19], ORB ( Oriented FAST and Rotated BRIEF ) – E. Rublee, V. Rabaud, K. Konolige, G. Bradski [20],

BRISK ( Binary Robust Invariant Scalable Keypoints ) – S. Leutenegger, M. Chli, R.Y. Siegwart [21], FREAK ( Fast Retina Keypoint ) – A. Alahi, R. Ortiz, P. Vandergheynst [22], A-KAZE ( Accelerated-KAZE ) – P. Alcantarilla, A. Bartoli, A. Davison [23, 24], LATCH ( Learned Arrangements of Three Patch Codes ) – G. Levi, T. Hassner [25].

• 1.1.    Дескриптор BRIEF

Метод BRIEF ( Binary Robust Independent Elementary Features ) [19] определяет преобразование (1), которое заключается в попарном сравнении пикселей (заранее сглаженной, например, фильтром Гаусса) области l размера s × s :

[ 1, P ⁽ x ) <  P ⁽ У ), t ( p , x , y ) =                                                (1)

( )’ [0,p(x) > p(y), где p(x) – интенсивность пикселя в точке с координатами x = (u, v) в области l. Набор таких пар пикселей (x, y) размера nd называется множеством «бинарных тестов». Таким образом, дескриптор особой точки определяется как nd -мерная битовая строка, определяемая по формуле:

f n -- ( P ) = Z ² i ^{- 1 T}( P , x, y i ) .                         ⁽²⁾

1 < i <  n_d

Величина n d выбирается равной 128, 256, 512. Важным является выбор пикселей в области для бинарного теста, в [19] авторы рассматривают пять методов определения векторов x и y :

• 1)    x и y выбираются случайным образом равномерно распределёнными;

• 2)    x и y выбираются случайно, согласно распределению Гаусса;

• 3)    x и y выбираются случайно в два этапа. Сначала согласно распределению Гаусса выбирается x относительно центра координат, затем y – относительно х ;

• 4)    x и y выбираются случайно на дискретной радиальной сетке;

• 5)    для каждой пары x выбирается в центре координат, а y – на дискретной радиальной сетке.

По результатам сравнения в [19] точность распознавания в пяти перечисленных случаях примерно одинаковая. Для сравнения дескрипторов используется уже известная мера Хэмминга.

Основными проблемами метода BRIEF является неоптимальный выбор точек для расчёта дескриптора и невозможность учитывать ориентацию точки при распознавании.

Рис. 1. Выбор точек для построения дескриптора

• 1.2.    Дескриптор ORB

Метод ORB ( Oriented FAST and Rotated BRIEF ) [20] призван устранить указанные выше недостатки BRIEF.

В методе ORB для расчёта ориентации угла используются координаты центра тяжести С , вычисляемые через моменты изображения m pq :

V о \ I m10 m 01 I m pq = Е x ^p y ^q I ( x , y ) C = 1---- ,---- I , x , y                    I m 00 m 00 )

тогда ориентация угла будет задаваться вектором, начало которого будет в центральной точке, а конец – в центре тяжести, а угол будет равен:

I m 01 I 0 = arctg I---- I .

( m i0 )

Эти идеи воплощаются в методе «steered» BRIEF. Для множества бинарных тестов размера n , с координатами ( x i , y i ) строится матрица S размерности 2 хn :

S =

x 1

y ₁

xn yn

Используя рассчитанный угол 0 , строится матрица вращения R 0 , и тогда можно получить матрицу S 0 с учётом поворота равную S 0 = R 0 S . Далее выполняется дискретизация угла с приращением 2 п /30, т.е. по 12 ° , и выполняется поиск и согласование дескриптора с S 0 .

Теперь дескриптор, в отличие от (2), будет иметь вид:

g n ( P , ⁰) = fd ( P )|( x , y ) e S 0 .

В [20] рассматривается проблема определения «качества» дескрипторов с точки зрения их последующего сопоставления. Ясно, что дескриптор некоторой однотонной области будет являться плохо различимым и коррелировать со многими другими. Поэтому предлагается оценивать качество дескрипторов через параметры среднего арифметического и дисперсии.

Метод BRIEF имеет важное свойство – каждый дескриптор имеет большую дисперсию и среднее значение около 0,5. Но как только дескриптор становится ориентированным по направлению ключевой точки, он теряет это свойство. Также важно, что бинарные тесты были некоррелированными, т.е. лучше распознавались. Чтобы разрешить эти проблемы, метод ORB использует поиск среди всех возможных бинарных тестов, чтобы найти те, которые имеют как высокую дисперсию, так и средние значения, близкие к 0,5, а также некоррелированные между собой. Результат называется rBRIEF. Для сопоставления дескриптора используется LSH ( Locality-sensitive hashing ) – метод понижения размерности многомерных данных.

• 1.3.    Дескриптор BRISK

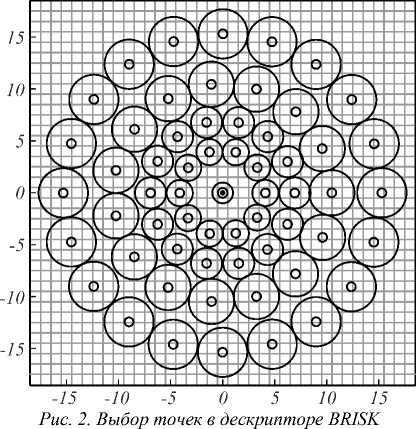
Для того, чтобы добиться инвариантности к вращению, в дескрипторе BRISK ( Binary Robust Invariant

Scalable Keypoints ) точки выбираются в соответствии с шаблоном на рис. 2.

Для вычисления ориентации ключевой точки вычисляется локальный градиент между парой точек ( p i , p j ) среди N ( N – 1)/2 точек области p .

g ( P i , P j ) = ( Pl - P j )

I ( P j , ^ j} ^- I ( P i , a )

II P i - P j II²

где I (P i , a i ) - сглаженные (по Гауссу) интенсивности точек со стандартным отклонением a i . На всем множестве пар точек А определяются «короткие пары» – S и «длинные пары» - L . У длинных - || P i - P j || <  5 _max, а у коротких – || p i – p j || >  § min , где § max , § min пороговые значения.

Длинные пары L используются для расчёта направления особой точки. Для вычисления ориентации определяется сумма всех «длинных градиентов»:

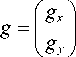
1 L

Е g ( P i -, P j ) ( P l , P j ) e L

и вычисляется a = arctg( g_y / g_x ). Сам бинарный дескриптор вычисляется, как и в BRIEF, но только для «коротких» пар. Сопоставление дескрипторов происходит аналогично предыдущим методам.

• 1.4.    Дескриптор FREAK

В дескрипторе FREAK ( Fast Retina Keypoint ) для расчёта дескриптора также используется круговая сетка, как и в BRISK. Отличие заключается в том, что плотность точек экспоненциально увеличивается к центру области, и они перекрываются между собой, см. рис. 3. Как в BRIEF и ORB, области особой точки предварительно сглаживаются.

Расчёт бинарного дескриптора происходит аналогично BRIEF. Предполагается, что не все пары будут полезны для эффективного описания дескриптора. Поэтому используется алгоритм выбора лучших пар, подобный ORB, путём максимизации дисперсии пар и минимизации корреляции.

Рис. 3. Выбор точек в дескрипторе FREAK

Интересно, что в полученных парах есть зависимость, соответствующая нашему пониманию модели сетчатки глаза человека. Человек для первоначальной оценки местоположения объекта использует перифо-веальные рецепторы, а затем, для уточнения, рецепторы из области фовеа. Аналогично, первые полученные пары найдены на внешнем радиусе области, а последние – во внутреннем [22].

В методе FREAK для сравнения дескрипторов используется каскадный поиск по каждым 16 байтам дескриптора. Причём более 90 % кандидатов отбрасываются при сравнении по первым 16 байтам, что существенно ускоряет поиск. Для оценки поворота особой точки суммируются локальные градиенты по выбранным парам, как и в BRISK.

• 1.5.    Дескриптор AKAZE

В этом методе [23, 24] описывается обнаружение и описание особых точек в нелинейных масштабных пространствах. Идея, лежащая в основе такого подхода, заключается в создании серии промежуточных изображений в разных масштабах (многомасштабное пространство) с помощью применения различного рода фильтрации исходного изображения.

Для построения нелинейного многомасштабного пространства на основе уравнений нелинейной диффузии было предложено использование схемы быстрой явной диффузии ( Fast Explicit Diffusion , FED).

Детектирование особых точек производится расчётом определителя матрицы Гессе для каждого отфильтрованного компонента нелинейных масштабных представлений L i исходного изображения.

Lh с2 UlL™ - ЦЛ, xx yy xy , где (Lxx, Lyy) – вторая производная по горизонтали и вертикали.

Для получения инвариантных дескрипторов вращения необходимо оценить доминирующую ориентацию в локальной окрестности особой точки. Как и в SURF, находится доминирующая ориентация в круговой области радиуса 6 с i с шагом дискретизации с i .

Для расчёта дескриптора используется модифицированная для нелинейного многомасштабного пространства версия дескриптора М-SURF. Для обнаруженной особой точки в масштабе с i вычисляются первая производная L x и L y в прямоугольной области 24 с i х 24 с i . На основе полученного генерального направления окрестности особой точки каждая область из рассматриваемой прямоугольной области поворачивается согласно полученному генеральному направлению. Дополнительно вычисляются производные в соответствии с этим направлением. В завершение полученный дескриптор нормализуется в 64битный вектор относительных единиц для достижения инвариантности к контрасту изображения [25].

• 1.6.    Дескриптор LATCH

Дескриптор LATCH разработан Г. Леви и Т. Хасснер [26]. Отличие метода LATCH от остальных состоит в том, что он использует триплеты точек, а не пары для расчёта дескриптора. В области особой точки вводится понятие мини-патча – это подмножество пикселей для расчёта бинарного дескриптора.

Чтобы создать дескриптор для 512 бит, в методе LATCH используется 512 триплетов, где каждый триплет определяет расположение трёх мини-патчей размера K × K , обычно 7×7. В каждом триплете один из мини-патчей обозначается как «якорь» P t , a , а два других мини-патча обозначаются как «компаньоны» P t ,1 и P t ,2 .

Для каждого из 512 триплетов s t авторы проверяют, является ли компаньон P t ,1 более похожим на якорь P t , a , чем второй компаньон P t ,2 . Для измерения сходства между патчами используется сумма квадратов разностей.

g ( W , S t ) =

1, P t ,

- P t дЕ >|| P , a - P t ,2 £

0, в остальных случаях .

Сопоставление дескрипторов выполняется через расчёт расстояния Хэмминга, как и в других методах.

Для выбора оптимального набора триплетов используется обучение по набору данных, из [27] (М. Браун). Набор данных содержит патчи, соответствующие одной и той же 3D-точке реального мира. Алгоритм был протестирован по тесту Миколайчика (Mikolajczyk).

2.    Выбор критериев и сравнение дескрипторов

Тест Миколайчика был представлен в [28, 29] и с тех пор стал популярным, он используется для оценки детекторов и дескрипторов особых точек изображений. Тест содержит изображения со следующими видами искажений: изменение точки обзора (Graf, Wall), изменение масштаба и поворот (Bark, Boat), JPEG-сжатие (Ubc), изменение освещения (Leuven), размытие (Bikes), (Trees) (см. рис. 4). Во всех изображениях есть малые смещения.

В тесте по изменению точки обзора положение камеры варьируется от фронтального положения до поворота на 60°. Поворот вокруг своей оси выполняется во всем диапазоне углов. Изменение масштаба и размытие достигаются изменением увеличения камеры и фокусировкой камеры соответственно. Масштаб изменяется примерно с коэффициентом 4. Изменение освещения выполняется путём изменения апертуры камеры. Последовательность JPEG генерируется с использованием параметров качества изображения от 40% до 2%. Каждая из тестовых последовательностей содержит 6 изображений с постепенным геометрическим или фотометрическим преобразованием. Все изображения имеют среднее разрешение около 800×640 пикселей.

Остановимся на выборе критерия сравнения. Основными свойствами особых точек являются: повторяемость, точность, информативность, локальность, количество, эффективность [30, 31].

Рис. 4. Тестовые изображения (сверху вниз: wall, ubc, trees, graf, boat, bikes, bark, leuven)

Для оценки качества дескрипторов используются следующие характеристики из [29]:

• – «корректные совпадения» ( correct matches ), СM – совпадения двух дескрипторов особых точек, отражающих одну точку реальной сцены;

  – «некорректные совпадения» ( false matches ), FM – совпадения двух дескрипторов особых точек, отражающих различные точки реальной сцены;

  – «общее количество совпадений» ( total number of matches ), ТNM – все совпадения между дескрипторами, равно сумме корректных и некорректных совпадений;

  – «соответствия» ( correspondences ), C – все действительные соответствия между особыми точками двух изображений, дескрипторы которых сравниваются.

Введём производные характеристики для последующей оценки:

– точность отклика ( precision ),

P = CM- , 1 - P = FM- ; TNM TNM

– полнота отклика ( recall ),

R = CM

C

.

Для оценки быстродействия ( эффективности ) предлагается использовать удельное время расчёта одного дескриптора T , полученное усреднением по всем точкам.

Нами выполнено измерение характеристик перечисленных дескрипторов. Схема эксперимента следующая: для ряда изображений (из теста Миколайчи-ка [28, 29]) выполняется обнаружение особых точек на двух изображениях с помощью детектора AKAZE, расчёт дескрипторов различными способами и их сопоставление методом полного перебора (« Brute Force »), а также расчёт проективного преобразования между изображениями с помощью функции find-Homography, для оценки количества действительных соответствий между точками. Для тестирования использовалась библиотека OpenCV 3.4.1 со стандартными параметрами функций. С практическими примерами и возможностями использования дескрипторов можно ознакомиться также в [32].

Эксперимент проводился на компьютере со следующими техническими характеристиками: процессор Intel Core i3-370М 2,4 ГГц, ОЗУ – 3 Гб, 64-разрядная операционная система, среда разработки Microsoft Visual C++ 2017.

Результаты оценки быстродействия дескрипторов

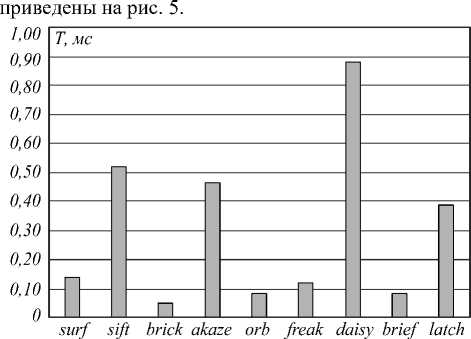
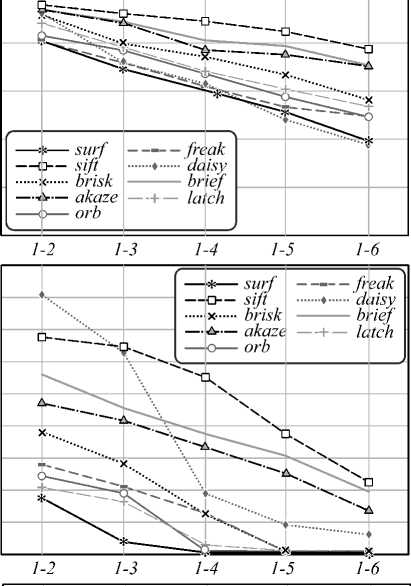
Рис. 5. Удельное время расчёта одного дескриптора

Оценка быстродействия выполнялась усреднённой по 48 изображениям. Из диаграммы видно, что для расчёта бинарных дескрипторов требуется меньшее время. Длительное время расчёта дескрипторов SURF, SIFT, AKAZE, DAISY объясняется более сложными расчётами. В данных методах вычисляется ориентация особой точки с использованием производных, что является вычислительно затратным, а также длительные способы сравнения дескрипторов.

В представленном наборе изображений насчитывается 6 изображений 8 сцен, снятых с различными искажениями. Первое изображение считается эталон- ным. На графиках на рис. 6 приведены результаты измерений. Дескрипторы первого изображения последовательно сравниваются с дескрипторами изоб- ражений со второго по шестое (это отражает ось абсцисс). Пример сопоставления дескрипторов можно увидеть на рис. 8.

0,3

0.2

0,1

а)

p

1,0

0,8

0,6

0,4

0,2

0 б)

—*— surf

—□— sift .....-x..... brisk

—д— akaze

—о— orb

—-— freak

—I— latch

—*— surf

—□— sift .

— akaze - orb - freak

в)

0.1

0 г)

—*— surf

—□— sift ......x-..... brisk —4s— akaze

—о— orb

—-— freak

—H — latch

—*— surf

—□— sift ......x-..... brisk —4»— akaze

—о— orb

—-— freak

.......♦......"daisy

------ brief

—+- latch

—*— surf

—□— sift ......x-..... brisk —^,— akaze

—o— orb

—-— freak

—ь — latch

—*— surf

—□— sift ......x-..... brisk —^— akaze

—о— orb

—-— freak

—H - latch

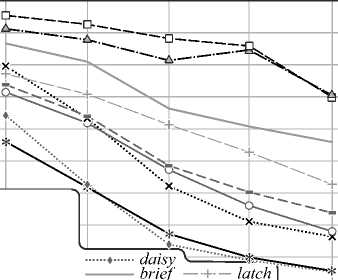
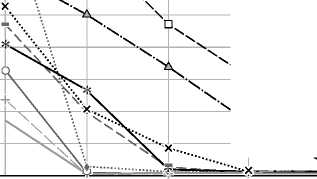
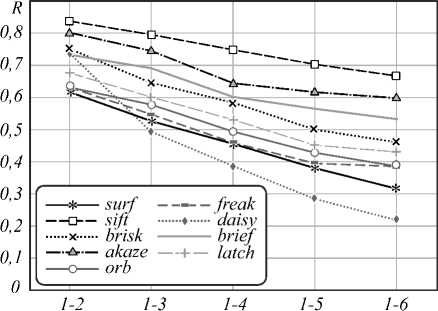
Рис. 6. Параметры P и R, вычисленные для пар изображений из разных наборов различными методами: Набор Bark (а), Набор Bikes (б), Набор Boat (в), Набор Graf (г), Набор Leuven (д), Набор Trees (е), Набор Ubc (ж), Набор Wall (з)

р

1,0

0.8

0,6

0,4

0,2

О

• д)

0.3 0.2 0.1

Р

0,8

0,7

0,6

0,5

0,4

О

• е)

Р

Окончание рис. 6

1,0

0,8

0.6

0,4

0,2

О

ж)

Р

0,5

0,4

0,3

0,2

0,1

О

з)

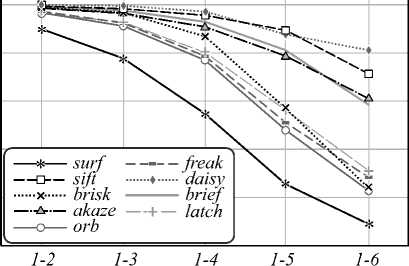
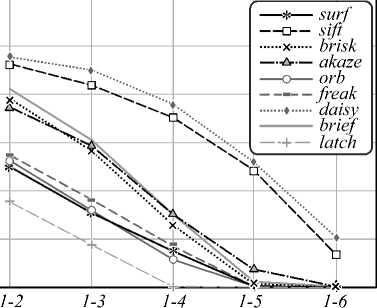
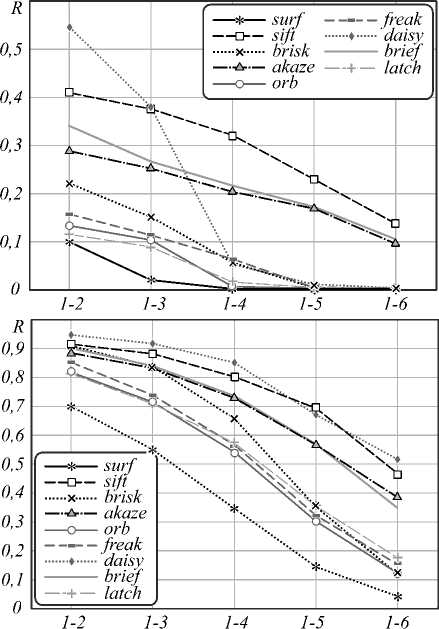
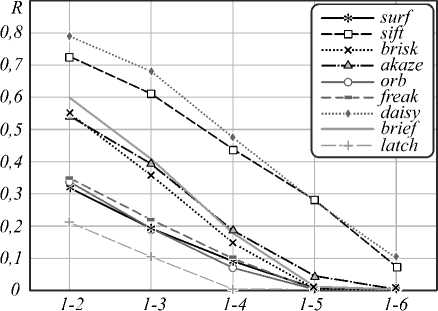
Общей тенденцией для всех сцен и дескрипторов является уменьшение значения точности отклика и полноты отклика при увеличении искажений. Также заметно подобие графиков P и R. Это объясняется зависимостью между параметрами C и TNM – обычно сопоставляется около 40–60% от общего числа обнаруженных особых точек.

Анализируя графики, можно заметить, что при вращении и изменении масштаба (рис. 6а, в) наибольшую инвариантность проявил бинарный де- скриптор AKAZE, в меньшей степени FREAK, BRISK. При повороте свыше 30° точность и полнота отклика всех бинарных дескрипторов (кроме AKAZE) стала минимальной и достигла нуля.

Изменение точки обзора (рис. 6 г , з ) в меньшей степени повлияло на точность методов AKAZE, BRISK, BRIEF, при этом, так как в случае 6 г имел место ещё и небольшой поворот изображения вокруг свой оси, дескриптор BRIEF оказался к нему не устойчив.

К искажениям типа размытия (рис. 6 б , е ) наиболее инвариантными являются методы AKAZE, BRIEF, BRISK. В случае 6 б – даже при сильном размытии параметры равнялись P = 0,15÷0,7, R = 0,05÷0,6.

Искажения, вносимые в процессе JPEG-сжатия (рис. 6 ж ), несущественно повлияли на дескрипторы AKAZE, BRIEF – для них минимальная точность отклика P – 0,6, а полнота отклика R – 0,4.

Для типа искажения «изменение освещения» (рис. 6 д ) все методы проявили наиболее высокую стойкость, наилучшие результаты показали методы AKAZE, BRIEF – для них минимальная точность отклика P – 0,7, а полнота отклика R – 0,5.

Можно заметить, что лучшие показатели точности и полноты отклика проявили для всех типов искажений именно небинарные дескрипторы – SIFT и DAISY. Это объясняется более сложными алгоритмами расчёта: дескрипторы вычисляются на основе градиентов в области особой точки, строятся в различных масштабах. Эти вычисления более длительны, что подтверждается рис. 5, но дескрипторы оказываются более точным.

3.    Оценка дескрипторов на конкретной задаче

Предлагаем рассмотреть вполне конкретную задачу машинного зрения, например, задачу отыскания корректного отображения одного изображения в другое с использованием исследуемых дескрипторов при заданном классе преобразований (масштаб-поворот, освещение, JPEG-сжатие, изменение угла обзора).

Для данной задачи сформирована база изображений, состоящая из 4 наборов. В каждый набор входит эталонное изображение, искажённое изображение (которое требуется найти), а также изображения - «дубликаты» (похожие изображения, но не идентичные), выбранные с помощью известной поисковой системы. Каждый набор насчитывает 10 изображений (рис. 7).

В качестве критерия соответствия изображений выберем максимизацию параметра P (точность отклика). Алгоритм расчёта аналогичен алгоритму в параграфе 2. Рассчитаем параметр P для каждой пары изображений в наборе. Результаты приведены в табл. 1–4. В каждом наборе изображение 1 соответствует только изображению 2. Видно, что в подавляющем большинстве случаев параметр P для изображений 1–2 является максимальным. Там, где это не так, происходит ошибка распознавания – эти столбцы выделены цветом. Ошибки распознавания обусловлены также тем, что дубликаты подобраны достаточно близко к оригиналу.

Больше всего ошибок распознавания произошло при поиске изображений с преобразованием масштаб-поворот: ORB, DAISY, BRIEF, LATCH и изменение угла обзора: SURF, FREAK. Тем не менее, при изменении угла обзора максимальное значение параметра P показал дескриптор DAISY. С учётом абсолютного времени выполнения программы наилучший результат для решения задачи в целом показал дескриптор AKAZE, SIFT. Это отчасти подтверждает полученный результат в пункте 2.

Рис. 7. Тестовые изображения

Табл. 1. Параметр P для набора изображений с преобразованием «масштаб-поворот»

	SURF	SIFT	BRISK	AKAZE	ORB	FREAK	DAISY	BRIEF	LATCH
1-2	0,244	0,719	0,158	0,498	0,015	0,194	0,026	0,005	0,004
1-3	0,006	0,009	0,006	0,006	0,006	0,006	0,012	0,007	0,006
1-4	0,004	0,005	0,005	0,004	0,005	0,004	0,009	0,004	0,005
1-5	0,005	0,006	0,005	0,005	0,004	0,004	0,009	0,005	0,004
1-6	0,003	0,004	0,003	0,003	0,003	0,003	0,006	0,003	0,003
1-7	0,025	0,026	0,021	0,021	0,022	0,024	0,036	0,028	0,023
1-8	0,02	0,024	0,022	0,02	0,022	0,022	0,034	0,021	0,02
1-9	0,023	0,021	0,015	0,016	0,017	0,017	0,027	0,017	0,014
1-10	0,005	0,005	0,005	0,004	0,004	0,005	0,008	0,004	0,005
Время,c	39,62	71,25	68,41	46,19	27,8	37,98	83,87	29,99	48,75

Табл. 2. Параметр P для набора изображений с преобразованием «изменение угла обзора»

	SURF	SIFT	BRISK	AKAZE	ORB	FREAK	DAISY	BRIEF	LATCH
1-2	0,261	0,83	0,545	0,575	0,31	0,361	0,895	0,609	0,169
1-3	0,003	0,004	0,003	0,003	0,003	0,003	0,005	0,004	0,002
1-4	0,029	0,041	0,029	0,03	0,028	0,028	0,046	0,03	0,03
1-5	0,08	0,08	0,084	0,076	0,076	0,075	0,095	0,076	0,076
1-6	0,226	0,2	0,207	0,207	0,207	0,207	0,217	0,207	0,194
1-7	0,455	0,455	0,455	0,455	0,455	0,455	0,5	0,5	0,545
1-8	0,143	0,143	0,146	0,163	0,158	0,163	0,25	0,146	0,143
1-9	0,052	0,071	0,057	0,06	0,067	0,056	0,125	0,067	0,05
1-10	0,01	0,018	0,011	0,008	0,009	0,01	0,018	0,011	0,008
Время,c	27,32	47,81	58,29	36,03	21,06	26,54	58,8	22,48	37,75

Табл. 3. Параметр P для набора изображений с преобразованием «освещение»

	SURF	SIFT	BRISK	AKAZE	ORB	FREAK	DAISY	BRIEF	LATCH
1-2	0,643	0,92	0,803	0,861	0,709	0,714	0,744	0,878	0,771
1-3	0,015	0,016	0,014	0,013	0,013	0,013	0,024	0,016	0,018
1-4	0,008	0,01	0,008	0,008	0,009	0,008	0,021	0,009	0,007
1-5	0,007	0,007	0,006	0,008	0,006	0,006	0,013	0,008	0,007
1-6	0,037	0,051	0,038	0,042	0,043	0,038	0,06	0,043	0,038
1-7	0,007	0,008	0,008	0,007	0,007	0,007	0,012	0,007	0,007
1-8	0,01	0,014	0,01	0,012	0,011	0,013	0,018	0,012	0,011
1-9	0,027	0,031	0,023	0,024	0,023	0,028	0,042	0,033	0,024
1-10	0,007	0,01	0,008	0,007	0,007	0,007	0,011	0,007	0,007
Время,c	23,1	35,39	53,38	31,35	19,09	23,28	48,89	19,31	27,86

Табл. 4. Параметр P для набора изображений с преобразованием «JPEG-сжатие»

	SURF	SIFT	BRISK	AKAZE	ORB	FREAK	DAISY	BRIEF	LATCH
1-2	0,769	0,984	0,975	0,968	0,918	0,93	0,993	0,979	0,925
1-3	0,007	0,008	0,007	0,007	0,008	0,007	0,016	0,007	0,006
1-4	0,005	0,005	0,005	0,005	0,005	0,005	0,009	0,005	0,004
1-5	0,01	0,013	0,009	0,009	0,009	0,008	0,017	0,014	0,009
1-6	0,004	0,005	0,004	0,004	0,004	0,004	0,006	0,004	0,004
1-7	0,012	0,014	0,01	0,009	0,009	0,011	0,018	0,01	0,009
1-8	0,036	0,041	0,04	0,035	0,041	0,037	0,069	0,038	0,045
1-9	0,146	0,15	0,17	0,174	0,178	0,149	0,175	0,152	0,156
1-10	0,069	0,07	0,052	0,058	0,071	0,058	0,113	0,081	0,058
Время,c	26,44	41,69	55,8	31,68	19,7	23,89	51,12	20,18	31,36

Рис. 8. Сопоставление точек методом AKAZE

Заключение

Анализируя полученные результаты, можно сделать следующие выводы. Искажения, вызванные поворотом изображения, изменением масштаба и точки обзора, вызывают наибольшее снижение показателей качества дескрипторов. Наилучшее качество по всем видам искажений показывают бинарные дескрипторы AKAZE, BRISK, BRIEF (рис. 6). Очевидно, что бинарные дескрипторы существенно выигрывают по быстродействию в сравнении с классическими дескрипторами (рис. 6), но при этом их точность ниже. Поэтому прослеживается некая обратная зависимость между качеством и быстродействием дескрипторов.

Поэтому основные усилия по повышению эффективности дескрипторов сконцентрированы по двум направлениям: повышение качества бинарных (BRIEF, ORB, BRISK, FREAK, LATCH, AKAZE) и вычислительная оптимизация методов SIFT, SURF (M-SURF, PCA-SIFT, GLOH, DAISY).

Быстродействие перечисленных алгоритмов уже позволяет использовать их в режиме реального времени. Однако для решения задач на аппаратной базе низкой производительности (мобильная робототехника, мобильные телефоны, одноплатные компьютеры) перечисленные методы требуют дальнейшего совершенствования.