Сравнение данных о положении Солнца

Вступление

Очевидно, что каждый хочет использовать самый простой и точный метод, но в этом случае оказывается, что эти два критерия довольно хорошо взаимоисключающие. Таким образом, тот, который вы выбрали, будет зависеть от некоторой комбинации того, насколько точным вам действительно нужно быть при выборе ресурсов, доступных для выполнения каждого из вычислений, и сколько времени вы хотите потратить на его реализацию.

Почему существуют различия?

Очевидно, что разные методологии будут давать несколько разные ответы из-за внутренней математики. Однако, даже используя точно такой же метод, два разных человека, скорее всего, получат два немного разных ответа для одной и той же ситуации.

Основными причинами этого являются вариации или несоответствия входных данных. Например, можно использовать Google Earth, чтобы получить широту / долготу для точного центра площадки до 12 знаков после запятой. Другой может использовать онлайн-базу данных, такую как infoplease или realestate3d, и искать только для города, достигая точности всего в 2-3 десятичных знака.

Еще одна проблема - индекс года, который используют все алгоритмы. Скорее всего, это будет скрыто за интерфейсом, который позволяет выбрать месяц и день, но результаты этого выбора будут преобразованы в один индекс для ввода. К сожалению, многие алгоритмы не являются ясными относительно того, требуется ли им индекс года в диапазоне 0-364 или 1-365 и должен ли он включать дополнительный день в високосный год. Кроме того, некоторые интерфейсы могут спросить вас о фактическом году расчета, в то время как другие просто предполагают текущий год или какой-либо другой.

Таким образом, базовый алгоритм может быть точно таким же, но разные интерфейсы могут подавать его индексы, которые выходят за один или два дня в зависимости от того, какой формат они принимают, и включают ли они правильное количество дополнительных дней в каждый високосный год и т.д.

Другой потенциальной проблемой при работе с записанными данными является определение точного времени, на которое рассчитывается каждый угол. Например, метеорологические данные, предназначенные для падающих солнечных излучений, обычно используют записи, усредненные за каждый час, неявно предполагая, что принимается соответствующая «средняя» или представительная солнечная позиция.

Это должно быть на середине между началом и концом каждого периода усреднения. Таким образом, для каждого полного часа дневного света это означает в полчаса (9:30, 10:30, 11:30 и т. Д.). В течение периода сразу после восхода солнца это означает на полпути между фактическим временем восхода и следующим целым часом. Точно так же за период, близкий к закату, представительное время находится на полпути между последним целым часом дневного света и фактическим временем захода солнца.

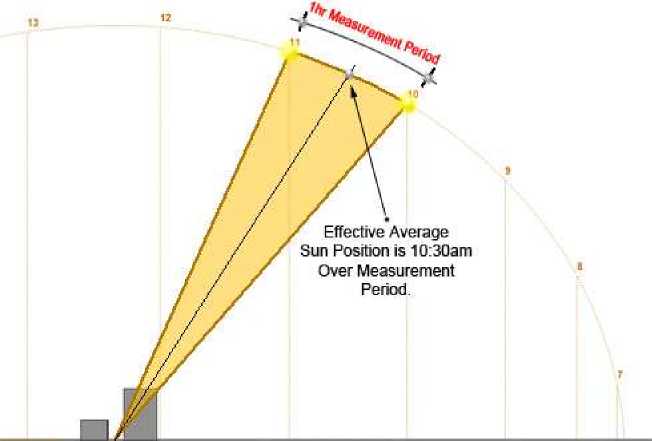
Рисунок 1 - Эффективное положение Солнца для среднечасовых измерений солнечной радиации.

Подробная информация, такая как эта, не всегда явна для всех записанных наборов данных о солнечных позициях, поэтому вам часто приходится делать некоторые эксперименты, чтобы определить, что вы должны использовать.

Положительные различия, возникающие в результате всего этого, как правило, довольно малы и обычно незначительны, учитывая приложения, к которым они применяются. Тем не менее, дело в том, что на самом деле очень сложно получить два набора данных о местоположении Солнца, чтобы они совпадали.

Сравнение углов

Сравнение фактических углов в каждом наборе данных звучит довольно тривиально, но это не так. Есть много примеров, когда два набора данных, которые настолько близки, что они по существу одинаковы, все равно будут вызывать большие различия в отдельных значениях. Причины для этого довольно очевидны, если вы думаете о них, но их еще нужно тщательно рассмотреть.

Периодическое вращение солнца

Солнце вращается вокруг Земли в непосредственной близости от кругового движения, поэтому солнечные углы являются периодическими. Таким образом, первая проблема, с которой приходится иметь дело, -обеспечить, чтобы в каждом наборе данных использовался один и тот же диапазон обертывания. Некоторые используют от -180 до +180, в то время как другие могут использовать от 0 до 360.

Это легко переносится в сравнении с использованием временных переменных и если / затем тесты, но вам нужно сделать это осторожно или вы закончите сравнение -150 ° с + 210 ° и получите некоторые довольно большие различия.

Следующая проблема возникает вокруг солнечного полудня, где азимутальный угол переключается с -179,9 до +179,9 в северном полушарии или с 359,9 до 0,1 в южном полушарии. Опять же, без некоторых тестов if / then прямое сравнение покажет их как 359,8 ° вместо 0,2 °.

Углы вблизи зенита

Другим источником потенциально больших различий является азимутальный угол, когда Солнце находится очень близко к зениту неба. Как показано на рисунке 2 ниже, по мере того, как Солнце проходит вблизи зенита, его азимутальный угол изменяется довольно значительно даже в течение всего нескольких минут. Таким образом, даже малейшая вариация в двух алгоритмах солнечной позиции может проявляться в таких условиях, как огромные азимутальные различия, когда в контексте реальная вариация -ничто.

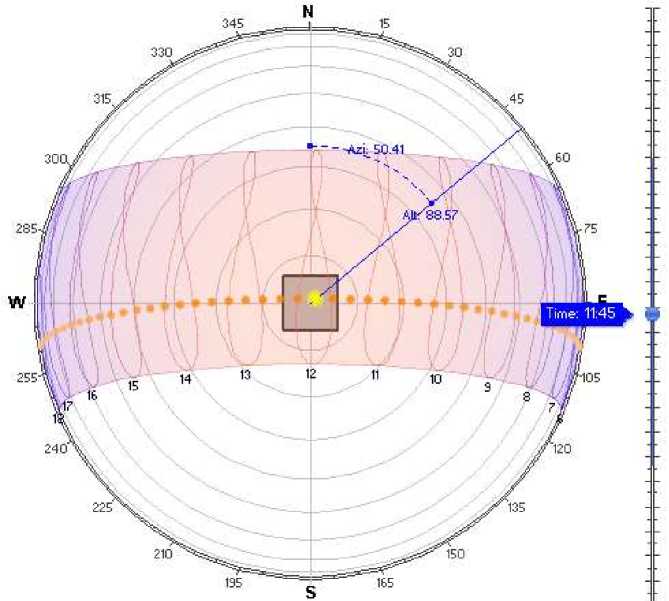
Рисунок 2 - Когда Солнце находится вблизи зенита, азимутальные углы значительно изменяются в пределах только 5-минутных шагов.

В качестве дополнительной иллюстрации на рисунке 3 показаны два положения солнца, которые очень близки, но по обе стороны от зенита, что дает азимутальные углы почти на 180 ° друг от друга.

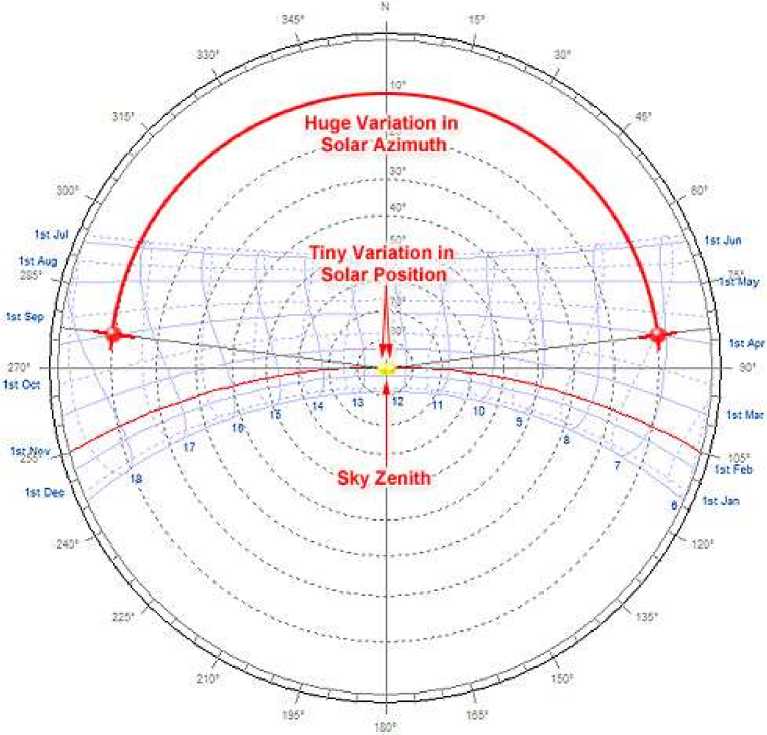
Рисунок 3 - Когда Солнце находится вблизи зенита неба, небольшая позиционная разница может часто приводить к большой разнице в азимутальном углу.

Таким образом, чтобы последовательно определять различия, важно учитывать как азимут, так и углы высоты вместе при сравнении, а не отдельно друг от друга.

Для согласованного сопоставления азимута на всех высотах вы можете просто умножить разность азимутального угла на косинус среднего угла высоты. Таким образом, когда оба положения Солнца близки к зениту, разность азимута умножается на число, близкое к нулю (cos (90 °) = 0), тогда как вблизи горизонта оно умножается на число, близкое к одному (cos(0°)=1).

Углы при закате / восходе

Конечно, умножение на косинус высоты подчеркивает любые различия азимута на горизонте. Это не проблема для мест между экватором и средними широтами (до 50 °). Однако, ближе к полякам, где Солнце очень низко в небе в течение дня, разница в времени восхода / захода солнца всего лишь на пару минут может привести к различию в азимутальном углу на 1-2 °. Это тривиальное различие в контексте, но значительно выше любого стандартного допуска теста.

Варианты здесь - это просто игнорировать значения ниже определенной высоты или пытаться исправить условия низкой высоты и высокой широты. К сожалению, для последнего варианта нет очевидного или «правильного» решения. Вы можете попробовать комбинацию взвешенных косинусов широты и высоты, но затем рискнуть отсутствием важных различий в средних широтах, где поправочные коэффициенты фактически маскируют значительные вариации. Вы можете экспериментировать с разными весами, но все это становится немного субъективным и довольно произвольным.

Мой подход состоял в том, чтобы использовать ступенчатый угол отсечной высоты, основанный на широте, но это так же произвольно и очень специфично для моего конкретного приложения.

Вывод

Непосредственное сравнение данных по положению Солнца кажется на поверхности довольно простым, но оказывается нагруженным контекстуальными погрешностями, о которых вам нужно знать. Эта статья объяснила, что такое эти погрешности и откуда они берут своё начало.