Сравнение формы фокусных пятен по интенсивности и потоку энергии для высокоапертурных зонной пластинки и спиральной зонной пластинки

Световые пучки с фазовыми и поляризационными сингулярностями активно исследуются в современной науке [1, 2]. Для их изучения был создан специальный раздел оптики – сингулярная оптика [3]. Одной из разновидностей таких пучков являются классические оптические вихри, содержащие сингулярность только в фазе [4– 10]. Проблемам их генерации [11 – 14], распространения [15– 18], фокусировки [19 – 22], регистрации [23 –25] посвящены работы ученых всего мира.

Для генерации оптических вихрей используются специальные элементы, такие как аксиконы [25], спиральные зонные пластинки (СЗП) [26–27] или метаповерхности [28–29], q- и s-пластинки [30–32]. Так, например, в [25] была предложена новая оптическая система на базе фазового аксикона для формирования азимутально и радиально поляризованных Бесселевых вихрей. В [26] рассматривается внедренная в кристалл сапфира СЗП, изготовленная с помощью остросфокусированного фемтосекундного импульса. Исследование оптических вихрей, сформированных серебряной СЗП, с помощью метода конечных разностей во временной области с учетом зависимости диэлектрической проницаемости от частоты (((FD)2TD)-метод) представлено в [27]. Было показано, что амплитудная СЗП может сформировать оптический вихрь с характеристиками, которые совпадают с характеристиками вихревого поля, формируемого фазовой СЗП. Лучшие результаты были показаны СЗП с рельефом из серебра, алюминия и хрома. Работа [29] посвящена исследованию острой фокусировки лазерного излучения спиральной металинзой из аморфного кремния. Численное моделирование также проводилось FDTD-методом. Топологический заряд и числовая апертура (NA) металинзы были равны 1. Формируемое в фокусе металинзой распределение интенсивности было практически круглым для TE-волны и в форме «пончика» для TM-волны. Теоретически было показано наличие областей обратного потока энергии в фокусе рассматриваемой металинзы, а эксперимент косвенно подтвердил теоретические выводы.

Область применения оптических вихрей включает оптические коммуникации [33–34], обработку материалов [35], ориентацию молекул [36], оптический захват и микроманипулирование [37–38], сенсорику магнитных полей [39] и т.д. В связи с этим исследования процессов их формирования и распространения являются очень актуальными. В частности, другими авторами не проводился подробный анализ эволюции оптического вихря, сформированного бинарной СЗП с фокусным расстоянием порядка длины волны, в ходе его распространения в свободном пространстве на расстояние порядка нескольких десятков микрон.

В этой статье мы приводим сравнительный анализ дифракции лазерного излучения на фазовых бинарных зонных пластинках (ЗП) и СЗП. Исследования проводятся с помощью моделирования в коммерческом пакете FullWAVE, реализующем FDTD-метод. В ходе исследования сравнивались поля, формируемые ЗП, освещаемой оптическим вихрем, и СЗП, освещаемой обычным Гауссовым пучком без фазовых сингулярностей. В первой части работы мы описываем ЗП и СЗП, падающее излучение и параметры моделирования. Далее в статье приведен подробный анализ сформированных дифракционных картин в фокальной плоскости элементов. Показано, что бинарная ЗП при фокусировке «ведет себя» почти как идеальная сферическая линза, в то время как из-за многолучевой структуры СЗП вблизи центра поток энергии в остром фокусе имеет несколько «лепестков», количество которых совпадает с топологическим зарядом СЗП, а на определенном расстоянии от фокуса лепестковая структура интенсивности (и потока энергии) заменяется на кольцевое распределение.

Постановка задачи

Рассмотрим бинарную ЗП с 13 кольцами. Радиус зон рассчитывается по формуле:

Г р = ^/ р X f + р 2 X 2/4, p = 1,2,3,..., P ,              (1)

где r_p - радиус зоны с номером р , X - длина волны падающего излучения, f – фокусное расстояние. Для расчета шаблона ЗП были выбраны следующие параметры: X = 0,532 мкм, f = X = 0,532 мкм (числовая апертура NA≈1), P =27 (общее количество зон, эквивалентное 13 кольцам). Шаблон ЗП представлен на рис. 1. Общий диаметр ЗП составляет порядка 16 мкм.

_г8 а)

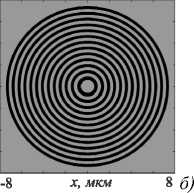
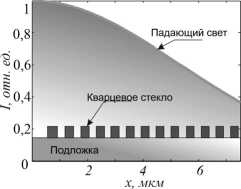
Рис. 1. Шаблон ЗП в поперечной (а) и продольной (б) плоскости и распределение интенсивности падающего

излучения (б)

В качестве материала рельефа ЗП выбрано кварцевое стекло (показатель преломления n = 1,5), тогда высота рельефа, согласованная с длиной волны h = λ / 2/(n – 1) ≈ λ. Линейно поляризованный Гауссов пучок с длиной волны λ =532 нм, радиусом перетяжки to = 8 мкм и внедренным в него оптическим вихрем с топологическим зарядом m выбран в качестве падающего излучения. Пространственное распределение амплитуды падающего на ЗП излучения с линейной поляризацией рассчитывалось с помощью автор- ского скрипта в MATLAB, задающего следующее распределение компонент падающего поля:

<

Г Г ² 1

E x ( г , 9 ) = exp -     exp ( im 9 ) ;

/to ² )

Ey (Г, 9) = 0, где (r, θ) – полярные координаты. Радиальное сечение интенсивности падающего поля на фоне сечения бинарного профиля рельефа ЗП представлено на рис. 1б.

При расчетах FDTD-методом использовались следующие параметры сетки: шаги по поперечным и продольной координатам составили 15 нм. Шаг по псевдовремени ct был выбран равным 7 нм в соответствии с условием Куранта. В ходе анализа результатов моделирования производилось усреднение поля по 10 периодам.

Также рассмотрим бинарную СЗП. Для расчета шаблона СЗП функция пропускания выбиралась в виде:

T ( r , 9 ) = sign {exp ^ im 9 + ik (^/ f ² + r ²

^^^^^^в

k – волновое число. Бинарный шаблон рассматриваемой СЗП, рассчитанный по формуле (3) для топологического заряда m =2, радиуса СЗП r =4 мкм и фокусного расстояния f = 0,532 мкм, представлен на рис. 2. Бинарный шаблон получается путем явного задания функции пропускания (3) в MATLAB: черные области на рис. 2 а соответствуют рельефу из кварцевого стекла высотой 532 нм, в серых областях рельеф отсутствует.

а)

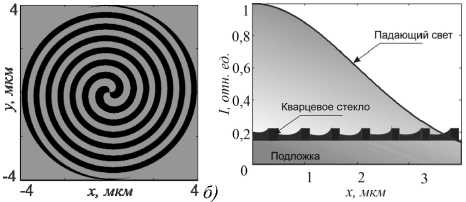
Рис 2. Шаблон СЗП (m = 2) в поперечной (а) и продольной (б) плоскостях

Рассматриваемые СЗП предполагаются быть изготовленными в кварцевом стекле. Гауссов пучок с длиной волны X = 0,532 мкм, радиусом перетяжки to = 4 мкм и линейной поляризацией рассматривался как падающее излучение. Пространственное распределение амплитуды падающего излучения с линейной поляризацией рассчитывалось с помощью авторского скрипта в MATLAB, задающего следующее распределение компонент падающего поля:

Г Г ² 1

E x ( r , 9 ) = exp - ; / to ² )

E y ( Г , ⁹) = 0.

Проекция интенсивности падающего поля на фоне сечения бинарного рельефа СЗП представлена на рис. 2 б . Параметры сетки были аналогичными, как и для ЗП.

Моделирование

Далее приведены результаты моделирования распределений интенсивности и потока энергии в фокусе для разных топологических зарядов.

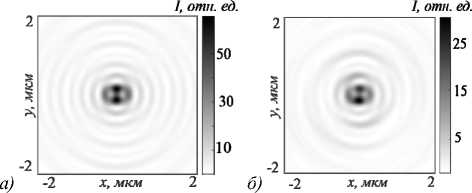
Рис. 3. Распределение интенсивности в плоскости XY на расстоянии теоретического фокуса f = λ от рельефа ЗП, освещенной оптическим вихрем (2) (а), и СЗП (б), освещенной Гауссовым пучком (4), при m = 1

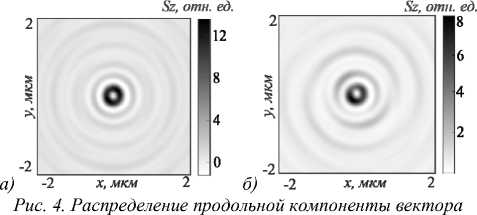
Умова–Поинтинга (потока энергии) в фокусе для ЗП (а), освещенной оптическим вихрем (2), и СЗП (б), освещенной Гауссовым пучком (4), при m = 1

На рис. 3 и 4 показаны распределения интенсивности и потока энергии в фокусе ЗП при освещении ее оптическим вихрем (2) с m = 1 (рис. 3 а , 4 а ) и СПЗ, освещенной Гауссовым пучком (4) (рис. 3 б , 4 б ). На рис. 3 видно, что по распределению интенсивности оба фокуса практически идентичны, а вот на рис. 4 уже начинают появляться различия. Если осевой поток энергии в фокусе у ЗП (рис. 4 а ) имеет вид почти симметричного светового кольца, то в фокусе СЗП (рис. 4 б ) поток энергии имеет вид неоднородного кольца с разрывом. Заметим также, что в центре распределения интенсивности (на оптической оси) в обоих случаях нет нуля интенсивности, а есть локальный минимум. Это происходит из-за ненулевого вклада продольной компоненты электрического поля. Но поток энергии вдоль оптической оси распространяться не будет.

Действительно, интенсивность поля может быть рассчитана по следующей формуле:

• I    = I x + l y + I z ,                                     (5)

где Ix = |Ex|2, Iy = |Ey|2, Iz = |Ex|2. При этом на оптической оси ненулевой будет только Iz. Продольная ком- понента вектора Умова-Поинтинга, отвечающая за поток энергии в направлении распространения света, определяется как:

S_z = Re Г E * H - E * H_x 1 , zxyyx

где H x и H y . – компоненты вектора напряженности магнитного поля. Из формулы (6) видно, что продольная компонента вектора Умова-Поинтинга определяется поперечными компонентами электромагнитного поля, а соответственно, на оптической оси она будет равна нулю, что согласуется с подробным исследованием поведения потока энергии в остром фокусе [40].

На рис. 5 и 6 показано то же самое, что и на рис. 3 и 4, но только при m = 2. Интересно, что отличия на рис. 5 противоположны различиям на рис. 6. Действительно, на рис. 5 а в фокусе у ЗП возникают два локальных максимума интенсивности на вертикальной оси, а на рис. 5 б в фокусе СЗП кольцо интенсивности, хотя и искажается, но не «разрывается» на два максимума. Для потока энергии, наоборот, осевой поток энергии в фокусе для ЗП (рис. 6 а ) имеет вид кольца, а поток энергии в фокусе для СЗП (рис. 6 б ) имеет два локальных максимума, лежащих на горизонтальной оси. Вдоль оптической оси световая энергия не распространяется.

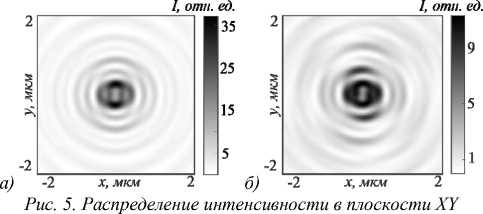
на расстоянии теоретического фокуса f = λ от рельефа ЗП, освещенной оптическим вихрем (2) (а), и СЗП (б), освещенной Гауссовым пучком (4), при m = 2

Sz, omu. ed.                             Sz, отн. ед.

• a)                              б)

Рис. 6. Распределение продольной компоненты вектора Умова–Поинтинга (потока энергии) в фокусе для ЗП (а), освещенной оптическим вихрем (2), и СЗП (б), освещенной Гауссовым пучком (4), при m = 2

На рис. 7 и 8 показано то же самое, что и на рис. 5 и 6, но при m =3. Интересно, что в фокусе СЗП и распределение интенсивности (рис. 7 б ), и осевой поток энергии (рис. 8 б ) имеют по три локальных максимума, расположенных в углах правильного треугольника. Хотя интенсивность в фокусе ЗП (рис. 7 а ) имеет только два локальных максимума, а поток энергии в фокусе ЗП (рис. 8 а ) имеет вид кольца.

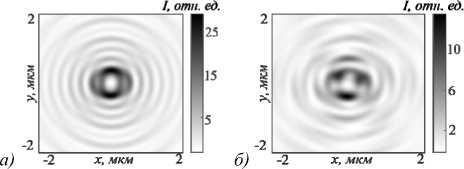
Рис. 7. Распределение интенсивности в плоскости XY на расстоянии теоретического фокуса f = λ от рельефа ЗП, освещенной оптическим вихрем (2) (а), и СЗП (б), освещенной Гауссовым пучком (4), при m = 3

Умова–Поинтинга (потока энергии) в фокусе для ЗП (а), освещенной оптическим вихрем (2), и СЗП (б), освещенной Гауссовым пучком (4), при m = 3

Обсуждение результатов

Из рассмотренных рис. 3–8 можно сделать некоторые выводы. Поток энергии в фокусе для высокоапертурной ЗП, освещенной оптическим вихрем с линейной поляризацией и топологическим зарядом m = 1, 2, 3, имеет вид кольца (рис. 4а, 6а, 8а). Так и должно быть в идеале, то есть при острой фокусировке идеальной сферической линзой оптического вихря с линейной поляризацией [41]. Распределение интенсивности в фокусе высокоапертурной ЗП, освещен- ной оптическим вихрем с линейной поляризацией и топологическим зарядом m = 1, 2, 3, имеет вид двух локальных максимумов, лежащих на вертикальной оси (направление начальной поляризации вдоль горизонтальной оси). Это видно из рис. 3а, 5а и 7а. Так и должно быть при идеальной острой фокусировке Гауссова пучка с любым оптическим вихрем [42]. Увеличение топологического заряда только приводит к увеличению расстояния между двумя вертикальными максимумами интенсивности. Таким образом, бинарная ЗП при фокусировке «ведет себя» почти как идеальная сферическая линза.

По-другому «ведет себя» СЗП разных порядков m = 1, 2 и 3 при фокусировке Гауссова пучка с линейной поляризацией. Из-за многолучевой структуры СЗП вблизи центра (при m =2 из центра СЗП выходят два «рукава» (рис. 2 а ), при m =3 из центра СЗП выходят три «рукава») поток энергии в остром фокусе (вблизи поверхности СЗП) также имеет несколько «лепестков»: при m = 1 световое кольцо имеет один разрыв (рис. 4 б ), при m =2 кольцо потока энергии имеет два разрыва или два максимума (рис. 6 б ), при m =3 кольцо потока энергии имеет три разрыва или три лепестка (рис. 8 б ). Под разрывом понимается отсутствие однородного (равномерного) распределения интенсивности в кольце, т.е. наличие явно выраженных пиков. В фокусе СЗП распределение интенсивности начиная с m =3 (рис. 7 б ) также приобретает многолепестковую структуру.

Но многолепестковая структура интенсивности и потока энергии, например, при m =3, показанная на рис. 7 б и 8 б , не сохраняется и при определенном расстоянии от СЗП пропадает.

Распределения продольной компоненты вектора потока энергии почти совпадают с распределениями интенсивности на этих расстояниях

На рис. 9 показаны распределения интенсивности в поперечной плоскости и вблизи оптической оси на разных расстояниях от СЗП ( m = 3) при освещении ее Гауссовым пучком с линейной поляризацией. Видно, что на расстоянии от фокуса ( z = 0,5 мкм) до расстояния z = 5 мкм трехлепестковая картина интенсивности сохраняется (рис. 9 а ). Причем из сравнения интенсивности в фокусе на рис. 7 б (или потока на рис. 8 б ) и интенсивности на расстоянии z = 5 мкм (рис. 9 а ) видно, что картина интенсивности вращается. При дальнейшем распространении света от СЗП вклад в световое поле будут давать уже не центральные «рукава», а периодические кольца СЗП

(рис. 2 а ), которые, как и спиральный аксикон [43 – 45], должны формировать кольцо при любом номере m . На рис. 9 б такое кольцо интенсивности формируется на расстоянии z = 15 мкм. Поскольку некоторая часть Гауссова пучка прошла за пределами апертуры СЗП, то, преломляясь на краях СЗП, Гауссов пучок сформировал фокус (световое пятно) на расстоянии z =23 мкм (рис. 9 в ). Заметим, что распределения интенсивности на рис. 9 почти не отличаются от распределения осевого потока энергии на этих расстояниях. Это подтверждает известное тождество между интенсивностью и потоком энергии для параксиальных световых полей [46].

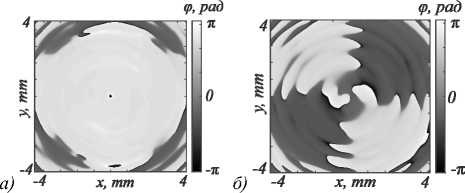
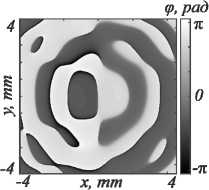
На рис. 10 показаны распределения фазы для компонент электромагнитного поля Ex, Ey и Ez. Из рисун- ка видно, что, несмотря на пройденное расстояние, пучок все еще содержит вихревую составляющую.

в)

Рис. 10. Распределение фазы в проекциях E x (а), E y (б) и E z (в) в плоскости XY на расстоянии 23 мкм от СЗП при m = 3

Заключение

В данной работе с помощью FDTD метода, реализованного в программном пакете FullWAVE, изучен процесс формирования и фокусировки оптических вихрей фазовыми бинарными ЗП и СЗП. В ходе исследования сравнивались поля, формируемые ЗП, освещаемой оптическим вихрем с Гауссовым распределением интенсивности, и СЗП, освещаемой обычным Гауссовым пучком без фазовых сингулярностей. Длина волны падающего излучения соответствовала зеленому лазеру и была равна 0,532 мкм. В работе рассматривались топологические заряды m = 1, 2, и 3. Было показано, что при острой фокусировке Гауссова пучка с линейной поляризацией и внедренным оптическим вихрем бинарная ЗП «ведет себя» почти как идеальная сферическая линза, в то время как при фокусировке Гауссова пучка из-за многолучевой структуры СЗП вблизи центра поток энергии в остром фокусе имеет несколько «лепестков», количество которых совпадает с топологическим зарядом СЗП, а на определенном расстоянии от фокуса лепестковая структура интенсивности (и потока энергии) сменяется на кольцевое распределение.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в частях «Моделирование» и «Обсуждение результатов», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части «Постановка задачи».