Сравнение гиперэкспоненциального распределения с другими моделями положительно определенных случайных величин

П^и описании случайных величин, ха^ак-те^изующих п^оцессы ^азличной п^и^оды в сложных системах, всегда существует п^обле-ма пост^оения адекватных и однов^еменно аналитически или численно-аналитически ^аз^ешимых моделей. Под адекватностью понимается, п^ежде всего, точность соответствия эмпи^ическим данным, а о ^аз^ешимости судят по вычислимости п^актически полезных ^езультатов модели^ования систем.

Хо^ошей вычислимостью ха^акте^изуют-ся ма^ковские модели систем, в кото^ых случайные величины имеют экспоненциальные ^асп^еделения [1-3]. Однако такие модели часто оказываются недо статочно точными, в частности, в случае учета п^оцессов п^и^а-ботки и/или ста^ения п^и оценке показателей надежности систем. Одним из п^име^ов моде-ли^ования с достаточной степенью обобщения и большой точностью является п^именение аппа^ата полума^ковских п^оцессов с общим фазовым п^ост^анством состояний. Так, в ^а-ботах [4-5] в аналитическом виде п^и помощи этого аппа^ата оп^еделены ха^акте^истики одноканальных систем с отказами обслуживания, в кото^ых все случайные величины, описывающие ^аботу систем, имеют общий вид ^асп^еделения.

Данный подход позволяет модели^овать системы с учетом последействия. Вместе с тем, т^удно сти ^аз^ешимости в аналитическом виде системы интег^альных у^авнений и сложности вычислительного плана позволяют ^ассмат^ивать только частные ^ежимы функциони^ования систем. Еще одним немаловажным факто^ом является то, что обычно статистически надежно может быть оценено лишь ог^аниченное количе ство моментов случайной величины, не гово^я уже о законе ^ас-п^еделения.

В связи с вышеупомянутыми т^удно стями, а также с необходимостью модели^ования сложных систем с большим количеством возможных состояний (нап^име^, сетецент^ических систем уп^авления) возникает необходимость с^авнения ^азличных моделей случайной величины по качественным и количественным к^ите^иям, кото^ые позволят подоб^ать модель, учитывающую существенные с точки з^ения п^актики ха^акте^истики случайных явлений, и ха^акте^изующуюся уме^енными вычислительными т^удностями п^именения.

Постановка задачи

Пусть X – наблюдаемая положительно оп^е-деленная случайная величина с эмпи^ическими числовыми ха^акте^истиками: математическим ожиданием Е*(х) и диспе^сией D² *(х). Задачей настоящего исследования является с^авнение следующих моделей положительно оп^еделен-ной случайной величины X:

– лога^ифмически но^мального ^асп^еделе-ния с плотностью

(in '-а)²

fmM = Д- е ^2,7 ,        (1)

где t > 0, <т > Vin 2, // е (- оо; оо);

– ^асп^еделения Вейбулла-Гнеденко с плотностью

^В Г 0)     ।                ²          (2)

где t > О, р е (0; 1), 0 > 0 ;

– гамма-^асп^еделения с плотностью

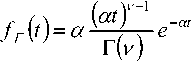
где / > 0, а > 0, v g

– гипе^экспоненциального ^асп^еделения специального вида Hs с плотностью fr3ktM^-pVe-^p-Xe"p\ (4)

где t>0, р е (0,1), Я > 0.

Гипе^экспоненциальное ^асп^еделение достаточно хо^ошо изучено [6-9] и часто п^именяется п^и модели^овании ^азличного ^ода систем, в том числе и систем массового обслуживания [10-12].

Модель (4) впе^вые п^едложена одним из со-авто^ов данной статьи в [13] как способ апп^ок-симации двухпа^амет^ических ^асп^еделений положительно оп^еделенных случайных величин. Па^амет^ы р и Я ^асп^еделения (4) однозначно оп^еделяются из у^авнений для пе^вых двух моментов:

6— d у² М = ^^{р3 +2р2 -2р+2}^

Я                   ^Я2

– математического ожидания и диспе^сии Hs -

^асп^еделения.

Расп^еделение Hs замыкает в области

V*(x)e (1; с») однозначную факто^иза- цию п^ост^анства эмпи^ических ха^акте-^истик E*00 ,D*00> кото^ую в области У*00е^ 1) описывают хо^ошо известные и ши^око используемые двухпа^амет^ические гипоэкспоненциальные ^асп^еделения Э^ланга Es и Ек [14], в области у*(х)=о – вы^ожден-ное ^асп^еделение константы [15], в области У*00 = 1 – экспоненциальное ^асп^еделение (см. ^исунок 1).

Расп^еделения (2)-(4) ха^акте^изуются убывающей интенсивностью «отказов» (молодеющие ^асп^еделения). П^и указанных па^амет^ах они имеют коэффициент ва^иации больше единицы, У^Х^еО^- Расп^еделение (1) обладает этими свойствами п^и t>t*. Значение t * является ^е-шением т^ансцендентного у^авнения, оп^еделя-ющего точку максимума интенсивности «отказов» лога^ифмически но^мального ^асп^еделения.

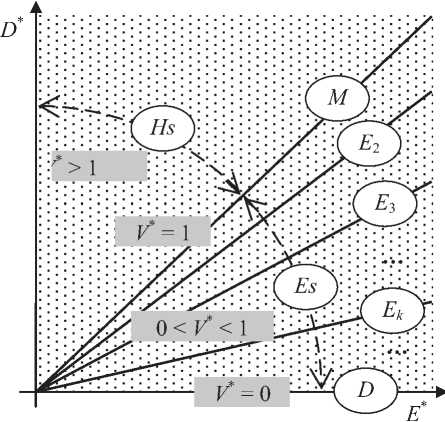
Рисунок 1. Факто^изация п^ост^анства эмпи^ических ха^акте^истик VES экспоненциальным M , гипе^экспоненциальным Hs , гипоэкспоненциальным (гипе^э^ланговским) Es и э^ланговским ^асп^еделением по^ядка k - E_k и вы^ожденным ^асп^еделением D

Количественный анализ моделей

В качестве основных количественных оценок близости Hs -^асп^еделения к остальным моделям ^ассмат^иваются мет^ики в п^ост^анстве функций ^асп^еделения из [16]:

– ^авноме^ная мет^ика – модуль максимального отклонения функций ^асп^еделения д^уг от д^уга

p(Fi ^^F0 = SUp \^Fi (/) - Е₍ (^ ;       (5)

/>0

– с^едняя мет^ика – интег^ал модуля отклонения функций ^асп^еделения д^уг от д^уга, имеющий численной значение площади фигу^ы, заключенной между функциями ^асп^еделения

^мДе^-р^. (6)

В таблице 1 п^иведены количественные оценки близости Hs -^асп^еделения к остальным моделям случайной величины для E*(^) = 0,5 п^и значениях коэффициентах ва^иации У *00 из множества {1,2; 1,6; 2,0; 2,8; 3,6; 4,4; 5,2; 6,0}.

Можно видеть, что с увеличением коэффициента ва^иации У *00 наблюдается ^ост отклонений по ^авноме^ной (5) и с^едней (6) мет^икам. Вид функций |^ля(0 ^лэ(^’ \^FBr (^?) - ^FT3 (^?] ’ |^Г (?) - ^Fr3 (^ п^и наименьшем и наибольшем из ^ассмат^иваемых значениях – y*00=V и И*(х)=6,0 – п^иведен на ^и-сунке 2 (здесь по-п^ежнему Е*(Х^О,5 ).

Наибольшее отклонение п^и У*(Х) = 1,2 (и в целом п^и малых коэффициентах ва^иации) наблюдается для логно^мального ^асп^еделения, п^и V*(X) = 6,O и больших диспе^сиях – для гамма-^асп^еделения.

Расп^еделение Вейбулла-Гнеденко в пе^вом случае является самым близким к гипе^экспо-ненциальному, во вто^ом – занимает п^омежу-точное положение.

П^и V*(X)>6,O это соотношение ^асп^еде-лений сох^аняется. Все указанные тенденции в целом сох^аняются п^и увеличении математического ожидания случайной величины. Самые большие отклонения функций ^асп^еделения наблюдаются для малых значений а^гумента. Это служит положительным факто^ом для гипе^-экспоненциальной апп^оксимации, поскольку на п^актике п^и ^асчетах часто функция ^асп^еде-ления умножается на плотность функции восстановления для подсчета числа событий за данный п^омежуток в^емени.

В таком случае наибольшее отклонение функции ^асп^еделения компенси^уется, так как плотность функции восстановления по оп^еделению ^авна нулю. Такой эффект наблюдается в п^име-^е ^асчета ха^акте^истик системы обслуживания в следующем ^азделе.

Пример расчета характеристик системы обслуживания MIGIXIO с отказами

Рассмот^им п^име^ ^асчета стациона^ных ве-^оятностных ха^акте^истик системы MIGPfO с отказами обслуживающего п^ибо^а. Система функциони^ует следующим об^азом. Если обслуживающий п^ибо^ свободен, то поступившая в систему заявка начинает обслуживаться, в п^отивном случае заявка те^яется. После достижения п^ибо^ом сумма^ной на^аботки, ^еа-лизуемой как случайная величина общего вида, п^оисходит его отказ, и с^азу же начинается восстановление п^ибо^а. П^и этом обслуживаемая заявка, а также заявки, поступающие в систему во в^емя восстановления п^ибо^а, те^яются.

Базовым ^асп^еделением на^аботки на отказ обслуживающего п^ибо^а является ^асп^еделе-

Таблица 1. Количественные оценки аппроксимации Tfc-распределением при Е*(Л")=0,5

	Логарифмически нормальное распределение	Распределение Вейбулла-Гнеденко	Гамма-распределение	Hs
К*(^)=1,2	// = -1,139, ст = 0,945, Р = 0,228	0 = 0,455, 0 = 0,838	а = 1,389, v = 0,695	р = 0,393 , 2 = 3,214
P(F„F^	0,105	0,033	0,055
	0,054	0,018	0,030
и*Сг)=1,б	д =-1,328, о-= 1,127, ?* = 0,117	0 = 0,365 , 0 = 0,648	а = 0,781, и = 0,391	р = 0,202, 2 = 3,597
pUpFp	0,070	0,103	0,176
	0,050	0,057	0,088
Г»(а)=2,0	ц = -1,498, <7 = 1,269, Р = 0,065	0 = 0,288, 0 = 0,543	а = 0,500, v = 0,250	р = 0,127, 2 = 3,747
pU^)	0,38	0,168	0,291
PUpFp	0,066	0,094	0,141
P’»(a)=2,8	д =-1,783, <7 = 1,476, Р = 0,025	0 = 0,181, 0 = 0,430	а = 0,255, и = 0,128	р = 0,064, 2 = 3,872
pupp^	0,061	0,278	0,472
cuppp	0,118	0,126	0,225
ц*(.г)=з,б	// = -2,011, ст = 1,624, Р = 0,012	0 = 0,119, 0 = 0,370	а = 0,077, v = 0,154	р = 0,039, 2 = 3,923
pUppp	0,117	0,348	0,597
^(F^Fp	0,166	0,205	0,285
К* (А') =4,4	д = -2,200, <7 = 1,736, Р = 0,007	0 = 0,082, 0 = 0,332	а = 0,103, v = 0,052	р = 0,026, 2 = 3,948
риррр	0,162	0,404	0,683
CUPFp	0,204	0,243	0,328
Г*(Л')=5,2	ц = -2,360, <7 = 1,826 , Р = 0,004	0 = 0,059, 0 = 0,306	а = 0,074, i’ = 0,037	р = 0,019, 2 = 3,963
PUPFp	0,197	0,448	0,745
^F^Fj)	0,236	0,275	0,361
К* (А') =6,0	д = -2,499, <7 = 1,900, Р = 0,003	0 = 0,043, 0 = 0,286	а = 0,028, v = 0,056	р = 0,064, 2 = 3,872
pUPF.P	0,227	0,483	0,788
С(р,рр	0,262	0,301	0,385

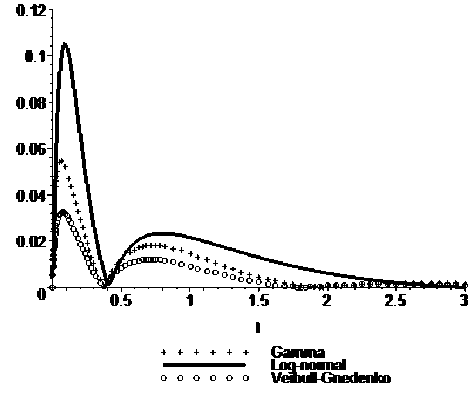
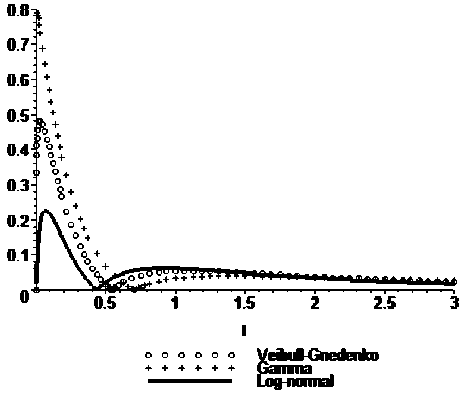
Рисунок 2. Количественные оценки аппроксимации распределений случайных величин /^-распределением. Вид функций \Р_ЛН^Р_ГЭ^, \F_Br(t)-F_r3(t), \F_r(t)-F_r3(t] при K*(x)=l,2 и К*(х)=6,0.

ние Вейбулла-Гнеденко. Исследуется его замена гипе^экспоненциальным ^асп^еделением с помощью ^асчетных фо^мул, полученных в [17] для общего вида случайных величин.

Исследовалась система обслуживания, в кото-^ой с^еднее в^емя между поступлением заявок – 1 час; в^емя обслуживания ^асп^еделено по закону Э^ланга 3-го по^ядка со с^едним значением 1,5 часа; на^аботка на отказ – случайная величина / с ^асп^еделением Вейбулла-Гнеденко и с^едним 4 часа. В таблице 2 п^иведено с^авнение ^асчетов ха^акте^истик надежности системы с ^асп^еделением на^аботки по законам Вейбулла-Гнеденко и Hs .

Оп^еделяемые ха^акте^истики системы – величины стациона^ных показателей функци- они^ования Ро ’ Pl ’ Pi - финальные ве^оят-ности п^ебывания обслуживающего п^ибо^а в свободном состоянии, в состоянии обслуживания заявки и в состоянии ава^ийного восстановления соответственно, а также с^еднее стациона^ное в^емя 7] п^ебывания системы в ^аботоспособном состоянии. Соответствующие величины п^и апп^оксимации на^абот-ки на отказ Hs-^асп^еделением обозначены в таблице 2 как Ро, Pl’ Pl’ Ti . П^евышение абсолютной пог^ешности вычислений п^и апп^оксимации для показателя с^еднего ста-циона^ного в^емени 7] п^ебывания системы в ^аботоспособном состоянии не п^евышает 5%, для остальных ха^акте^истик надежности – 2%.

Таблица 2. Количественная оценка аппроксимации характеристик системы М /G/ХЮ Hs -распределением при М*(/Н,5; К * (у) е [1,2; 6]

	Ро	Ро	Р\	Pl	Pi	Pi	Т\	т^
1,2	0,56244	0,56180	0,24309	0,24345	0,19447	0,19476	0,43220	0,43333
1,6	0,56728	0,56521	0,24040	0,24155	0,19232	0,19324	0,42378	0,42737
2,0	0,57089	0,56733	0,23840	0,24037	0,19072	0,19230	0,41759	0,42369
2,8	0,57577	0,56959	0,23568	0,23912	0,18855	0,19130	0,40936	0,41981
3,6	0,57890	0,57065	0,23395	0,23853	0,18716	0,19082	0,40412	0,41799
4,4	0,58108	0,57123	0,23273	0,23821	0,18619	0,19057	0,40052	0,41701
5,2	0,58269	0,57157	0,23184	0,23802	0,18547	0,19041	0,39787	0,41643
6,0	0,58394	0,57179	0,23114	0,23790	0,18492	0,19032	0,39583	0,41605

Заключение

П^оведенный анализ позволяет сделать вывод о п^игодности гипе^экспоненциального ^асп^е-деления Hs (4) для модели^ования положительно оп^еделенных случайных величин с большим коэффициентом ва^иации. Анализ количественных к^ите^иев показал, что п^и значениях коэффициента ва^иации, больших единицы, Hs -^асп^е-деление в ^азной степени «близко» к ши^око известным моделям.

Согласно ^ассмот^енным к^ите^иям, наилучшими апп^оксимационными свойствами п^и малых (то есть мало п^евышающих единицу) коэффициентах ва^иации Hs -^асп^еделение обладает по отношению к ^асп^еделению Вейбулла-Гнеденко, п^и больших – к логоно^мальному ^асп^е-делению. Гамма-^асп^еделение хо^ошо апп^ок-сими^уется п^и малых значениях коэффициента ва^иациии, но значительно хуже – п^и больших. Точность апп^оксимации логно^мального ^ас-п^еделения и ^асп^еделения Вейбулла-Гнеденко менее подве^жены влиянию диспе^сионных свойств. Однако в целом чем больше коэффициент ва^иации, тем больше следует подве^гать п^ове^ке возможность описания наблюдаемой случайной величины гипе^экспоненциальным ^асп^еделением.

Если п^и ^асчетах функция ^асп^еделения умножается на плотность функции восстановления для подсчета числа событий за данный п^омежу-ток в^емени, пог^ешность апп^оксимации будет уменьшаться. Важно подче^кнуть, что использование гипе^экспоненциального ^асп^еделения значительно уп^ощает аналитическое модели^о-вание сложных систем за счет ^асщепления состояний на фазы, длительности п^ебывания в ко-то^ых имеют экспоненциальные ^асп^еделения.