Сравнение исходной и оптимизированной систем векторного управления методом компьютерного моделирования

Общие сведения

Полная формулировка темы: модернизация системы ПОУ (полеориентированного управления) посредством взаимной коррекции намагничивающей и моментообразующей составляющих статорного тока и ее сравнение с классическим вариантом посредством компьютерного моделирования в цикле работы привода, включающем рекуперативный режим.

Цель работы: обеспечить максимально энергоэффективный генераторный режим работы привода при условии внесения минимальных изменений в систему ПОУ и минимальной дозагрузки вычислительного устройства.

Методы: построение компьютерных имитационных моделей ПЧ-АД с ПОУ с коррекцией и без нее и исследование влияния коррекции на параметры привода и энергетические характеристики системы.

Особенность модернизации заключается в поддержании определенного соотношения между намагничивающей и моментообразующей составляющими статорного тока. Ввиду научного интереса к поведению системы с коррекцией в рекуперативном режиме в данной работе это соотношение поддерживается приблизительно на уровне, рекомендованном источниками [1–3]. Если в источниках [1–3] рассматривалась система с под- держанием угла между током статора и потокосцеплением ротора на уровне 45°, то в данной работе в связи с особенностями подбора коэффициента между намагничивающей и моментообразующей составляющими статорного тока в генераторном режиме работы привода этот угол поддерживается на уровне 50°. Присутствует небольшое отклонение, что, однако, не мешает модернизированной системе продемонстрировать лучшую энергоэффективность по отношению к исходному варианту. Это подтверждается графиками, полученными в ходе компьютерной имитации.

Функциональная схема рассматриваемой системы ПОУ АД представлена на рис. 1.

Задание на скорость проходит через задатчик интенсивности. Затем с учетом сигнала обратной связи подается на регулятор скорости. Затем следует блок ограничения и блок пересчета момента в моментообразующую составляющую тока. С учетом обратной связи по моментообразующему току задание подается на ПИ-регулятор тока. После этого следует фазный преобразователь координат, переводящий сигналы от моментообразующего и намагничивающего контуров в сигналы управления на блок формирования ШИМ. Касаемо контура намагничивания, стоит отметить, что он начинается с задания на потокосцепление ротора, проходящего впоследствии через задатчик интенсив-

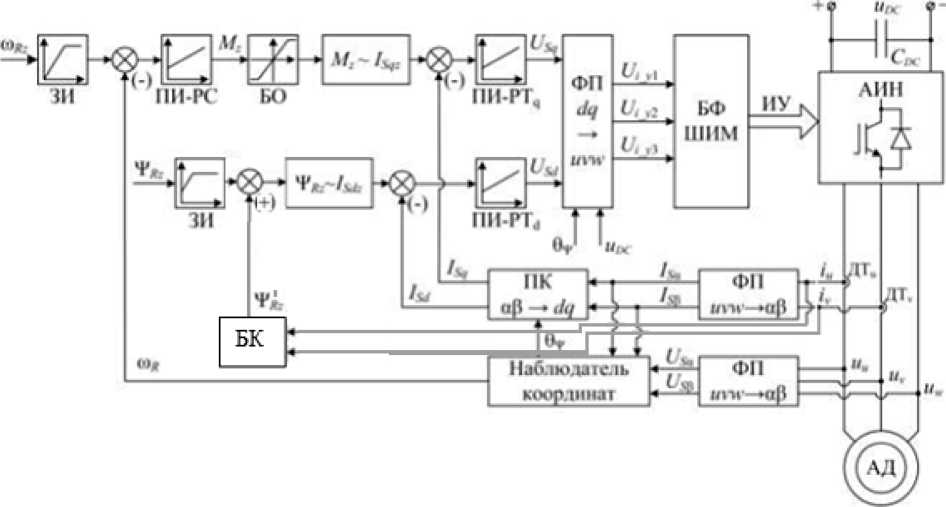
Рис. 1. Функциональная схема ПОУ АД:

АИН - автономный инвертор напряжения; u DC - напряжение питания инвертора; ДТ u , ДТ v - датчики фазных токов двигателя; ФП - фазный преобразователь координат; ПК - преобразователь систем координат; ПИ-РС, ПИ-РТ - пропорционально-интегральные регуляторы скорости и тока; БО - блок ограничения заданного электромагнитного момента; ЗИ - задатчик интенсивности; БК – блок коррекции; БФ ШИМ - блок формирования широтно-импульсной модуляции;

ИУ - импульсы управления транзисторами АИН

Fig. 1. Functional diagram of the FOC AM:

AIN – autonomous voltage inverter; u DC – inverter supply voltage; DTu, DTv – motor phase current sensors; PF – phase coordinate converter; PC – coordinate system converter; PI-RS, PI-RT – proportional-integral speed and current regulators; BO – set electromagnetic torque limiter block; ZI – intensity setter; CU – correction unit; BF PWM – pulse-width modulation formation block;

IS – control pulses of AIN transistors

ности. Затем – блок пересчета потокосцепления ротора в ток намагничивания. С учетом обратной связи по намагничивающему току сигнал подается на ПИ-регулятор и на фазный преобразователь, о котором сказано выше.

Компьютерная модель, построенная в соответствии с функциональной схемой (см. рис. 1) с дополнительным блоком (обведен красной линией) расчета взаимной коррекции моментообразующей и намагничивающей составляющих статорного тока, представлена на рис. 2.

На основании проанализированных работ отечественных [1–3] и зарубежных авторов [4–6] была выдвинута гипотеза о повышении энергоэффективности системы «Обратимый преобразователь частоты – асинхронный двигатель» путем взаимной коррекции намагничивающей и моментообразующей составляющих обобщенного вектора тока статора асинхронного двигателя [7], сводящейся к поддержанию этих величин на близком уровне без серьезного ущерба для устойчивости системы. Здесь и в дальнейшем условимся считать, что φ′ – угол между намагничивающей и моментообразующей составляющими статорного тока [8, 9].

За основу принят асинхронный двигатель с короткозамкнутым ротором [10], характеристики которого представлены в таблице.

Обратимый преобразователь частоты [11] состоит из выпрямителя на базе IGBT, звена постоянного тока с конденсатором, служащим для уменьшения пульсаций выпрямленного напряжения, инвертора на базе IGBT.

Модель [12], силовая и измерительная части которой показаны на рис. 3, имитирует работу грузоподъемного устройства (привода подъема крана) на временных отрезках:

0,2–0,7 с – разгон на холостом ходу (подъем крюка до натяжения цепей);

0,7–1 с – работа в статике с постоянной скоростью (подъем крюка до натяжения цепей);

• 1    с – наброс момента, соответствующего массе поднимаемого груза (точка полного натяжения цепей);

• 1 –1,5 с – работа с моментом, соответствующим массе поднимаемого груза, и фиксированной скоростью (равномерный подъем груза);

• 1 ,5–2 с – работа с моментом, соответствующим массе поднимаемого груза, и снижением скорости (подъем груза с замедлением);

  

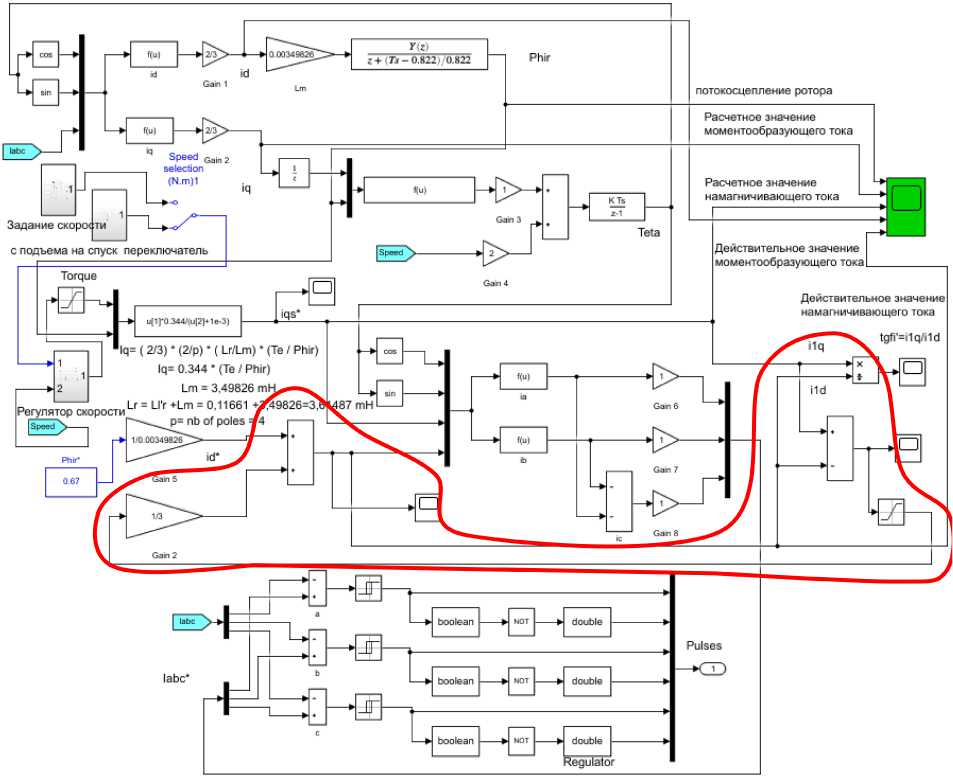
  Рис. 2. Модель модернизированной системы ПОУ Fig. 2. A model of the modernized FOC system

  
  

Характеристики АДКЗ

Characteristics of the squirrel-cage asynchronous motor

Параметр	Значение	Единица измерения
Номинальная мощность	160	кВт
Номинальное напряжение	400	В
Номинальная частота	50	Гц
Сопротивление цепи статора	0,0057	Ом
Индуктивность цепи статора	0,09612	мГн
Сопротивление цепи ротора	0,0044	Ом
Индуктивность цепи ротора	0,11661	мГн
Взаимная индуктивность	3,49826	мГн
Момент инерции	2,326	кг·м2
Коэффициент трения	0,05658	–
Число пар полюсов	2	–

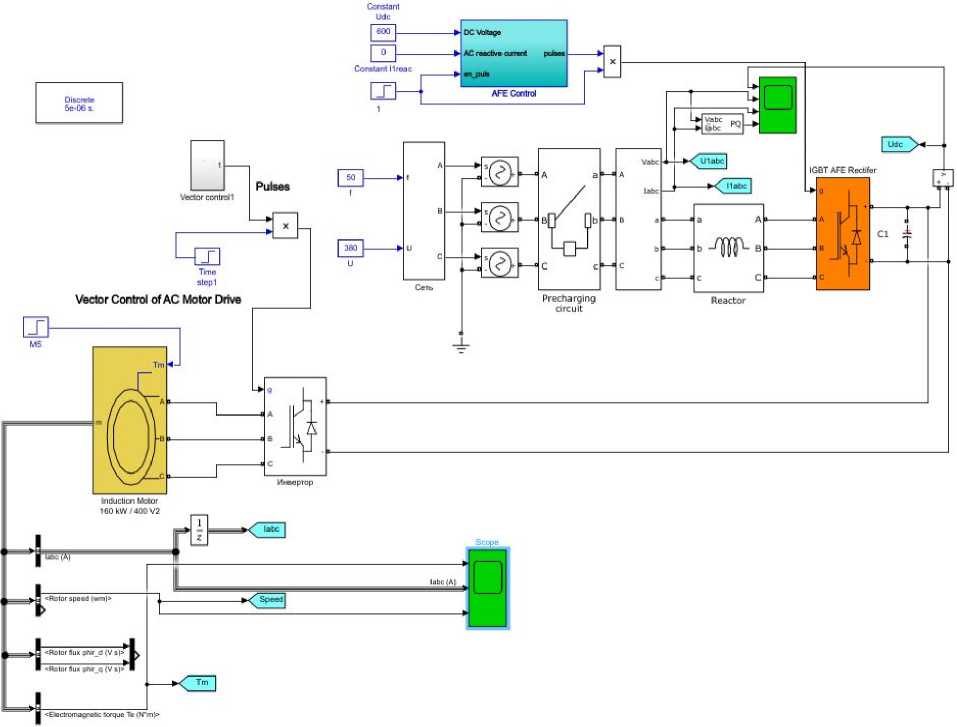
Рис. 3. Модель ПЧ-АД

Fig. 3. A model of the frequency converter – asynchronous motor

• 2–2,5 с – работа с моментом, соответствующим массе опускаемого груза, и ускорением (опускание груза с разгоном);

• 2,5–2,7 с – работа с моментом, соответствующим массе опускаемого груза, и фиксированной скоростью (опускание груза с установившейся скоростью);

• 2,7–3,2 с – работа с моментом, соответствующим массе опускаемого груза, и замедлением (опускание груза с замедлением);

• 3,2–3,7 с – работа с моментом, соответствующим массе удерживаемого груза, и нулевой скоростью (удержание груза).

Схема без коррекции

Графики момента, трехфазного тока статора и скорости представлены на рис. 4.

Рис. 5 иллюстрирует график потребления активной энергии. За все время моделирования (3,7 с) с учетом рекуперации было израсходовано 22 кВтс.

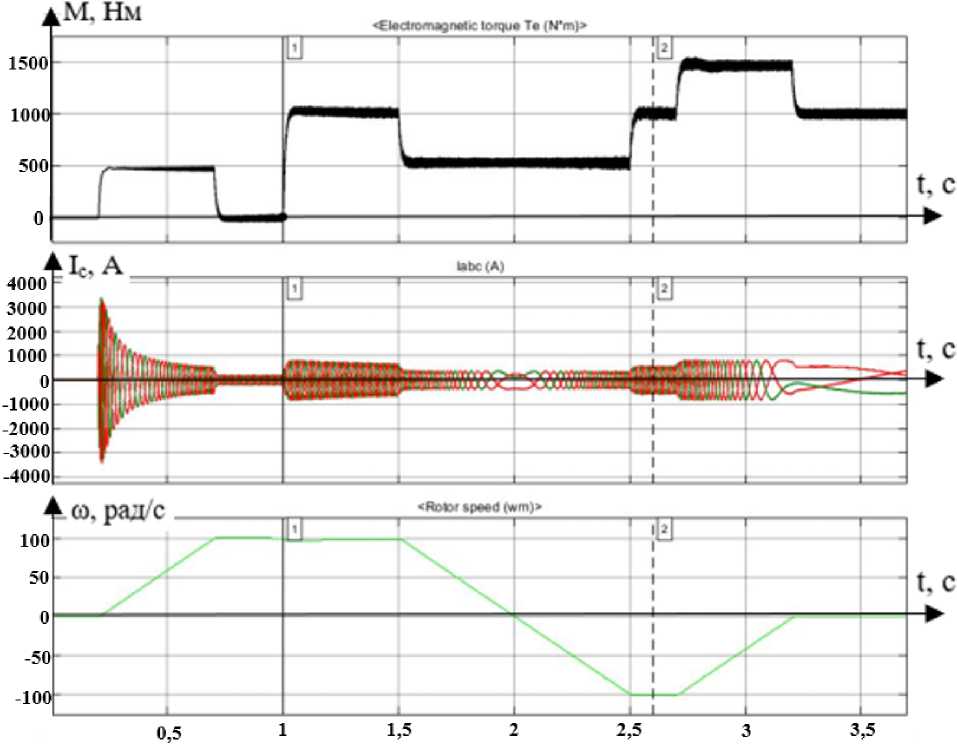
Рис. 4. Графики момента, трехфазного тока статора и скорости Fig. 4. Graphs of torque, three-phase stator current, and speed

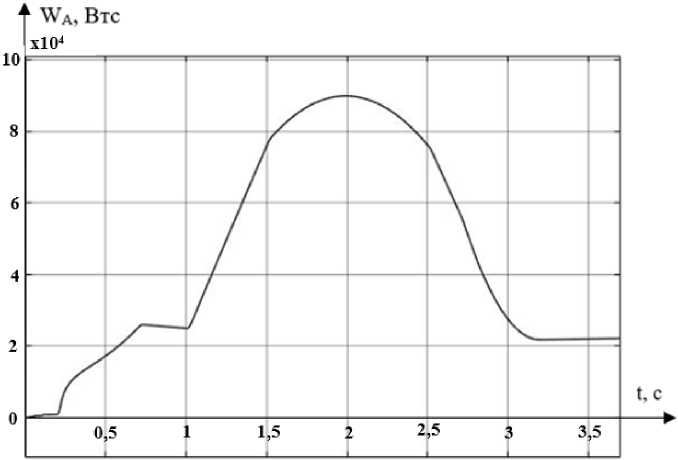
Рис. 5. График потребления активной энергии Fig. 5. Active energy consumption graph

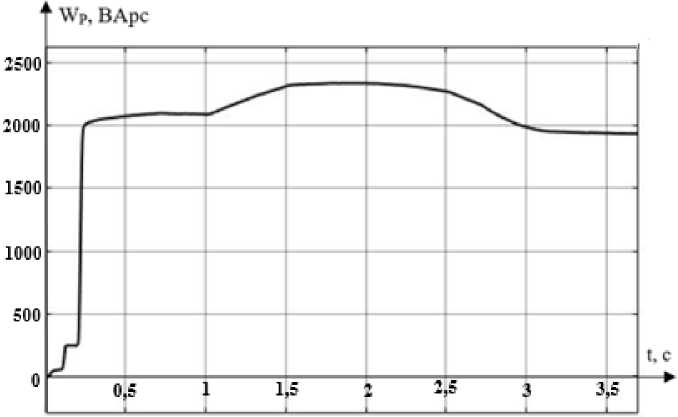
Рис. 6. График потребления реактивной энергии Fig. 6. Reactive energy consumption graph

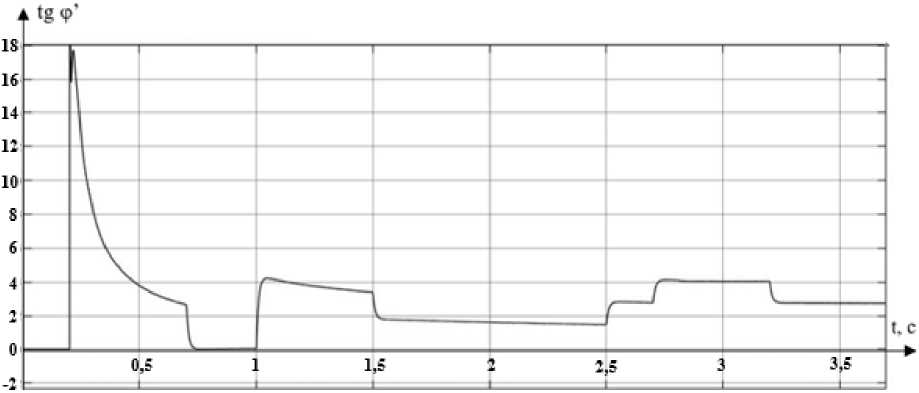
Рис. 7. График tg φ′

Fig. 7. Graph of tg φ′

Рис. 6 показывает график потребления реактивной энергии. За все время моделирования (3,7 с) с учетом рекуперации было израсходовано 1950 ВАрс.

Ниже на рис. 7 приведен график tgφ′.

В установившемся режиме tgφ′ принимает значения в диапазоне от 0 до 4. За контрольную точку для сравнения возьмем значение в момент времени 2 с. Для схемы без коррекции показатель tgφ′ в этой точке составляет около 1,7.

Схема с коррекцией

Сразу поясним, что коррекция заключается в нахождении разности мгновенных значений моментообразующей и намагничивающей составляющих статорного тока, умножении этой разности на масштабирующий коэффициент и приращении полученного значения к намагничивающей составляющей (см. рис. 2). На основании принципа построения системы со взаимосвязанными контурами моментообразующая составляющая при этом подстраивается под намагничивающую, чтобы их взаимное влияние обеспечило работу привода с заданной скоростью и поддержанием требуемого момента. Графики момента, трехфазного тока статора и скорости представлены на рис. 8.

Рис. 9 иллюстрирует график потребления активной энергии. За все время моделирования (3,7 с) с учетом рекуперации было израсходовано 9 кВтс.

Рис. 10 показывает график потребления реактивной энергии. За все время моделирования (3,7 с) с учетом рекуперации было израсходовано 1400 ВАрс.

Ниже на рис. 11 приведен график tgφ′.

В установившемся режиме tg φ′ принимает значения в диапазоне от 0 до 2. Для схемы с коррекцией показатель tg φ′ в точке 2 с составляет около 1,2.

Во временном диапазоне 1,6–2 с тангенс под- держивается на уровне около 1,2, что соответству ет углу между намагничивающей и моментообра зующей составляющими тока статора около 50°.

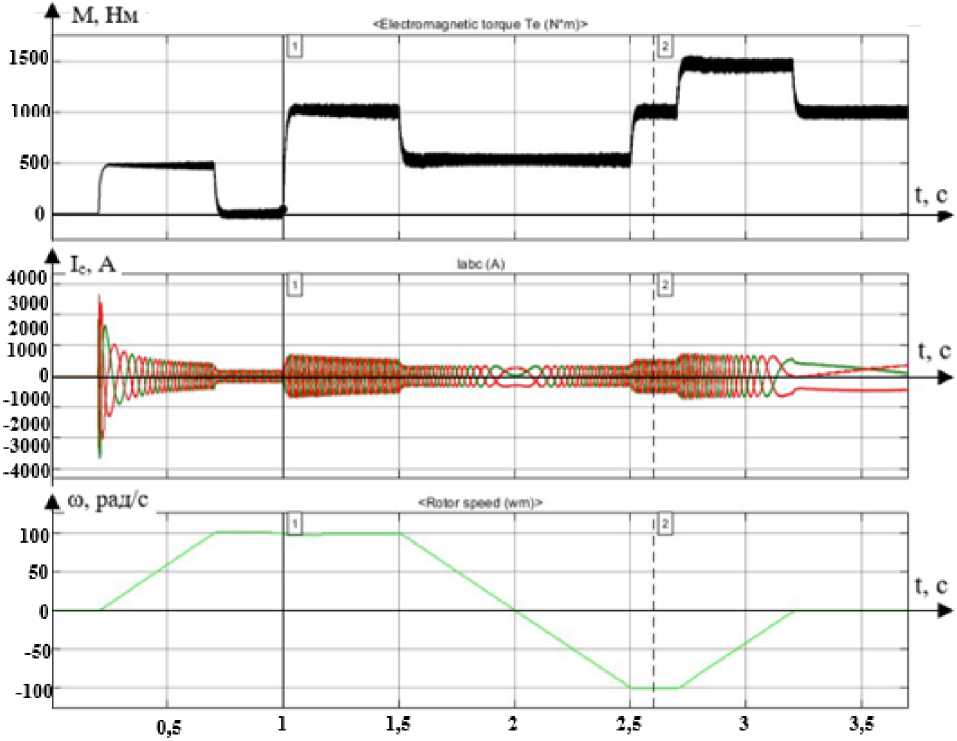
Рис. 8. Графики момента, трехфазного тока статора и скорости Fig. 8. Graphs of torque, three-phase stator current, and speed

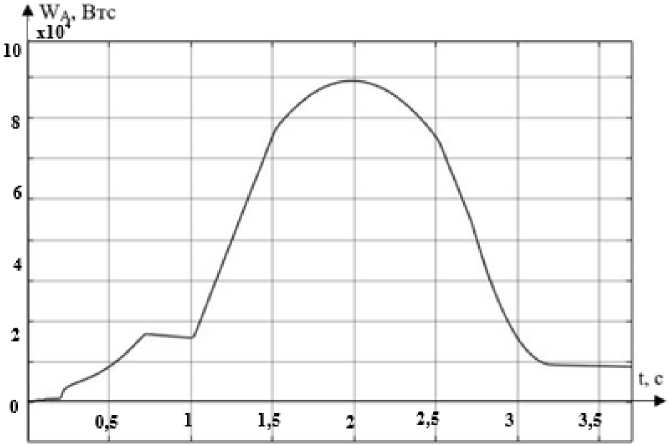
Рис. 9. График потребления активной энергии Fig. 9. Active energy consumption graph

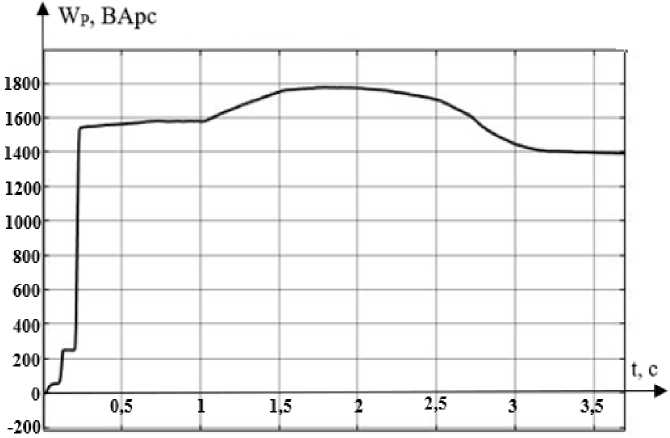
Рис. 10. График потребления реактивной энергии Fig. 10. Reactive energy consumption graph

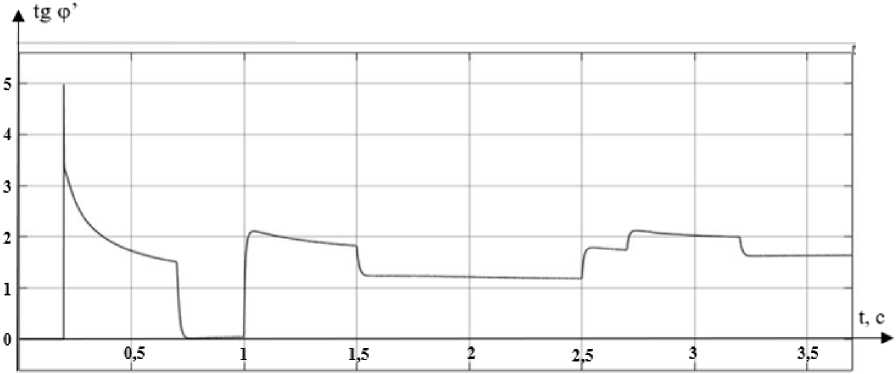
Рис. 11. График tg φ′

Fig. 11. Graph of tg φ′

Преимущества и недостатки использования схемы с коррекцией

Касаемо отличий, наибольшую ценность представляют следующие выводы.

Первое, что стоит отметить, глядя на графики потребления активной электроэнергии, это разница в пиковом значении около 10 000 кВтс (80 000 кВтс у доработанной схемы против 90 000 кВтс у исходной, что является ощутимым отличием). Второе – меньшее потребление активной электроэнергии схемой с коррекцией во всем временном диапазоне моделирования. За цикл эта разница составляет 13 кВтс.

По мнению авторов работ [1–3], эта разница обусловлена введением корректирующего сигнала, обеспечивающего приближение tgφ′ к 1 в тех режимах, когда это не противоречит стабильной работе привода. Что и было реализовано в модернизированной схеме.

Также уменьшилось потребление реактивной энергии на 550 ВАрс.

Отсюда следует вывод о том, что применение взаимной коррекции намагничивающей и моментообразующей составляющих в системе «обратимый преобразователь частоты – асинхронный двигатель» положительно сказалось на повышении энергоэффективности. То есть в общем основная цель исследования в рамках выдвинутой гипотезы достигнута.

При этом был обнаружен недостаток, связанный с показателями устойчивости и выраженный в увеличении пульсаций момента на величину около 15 %. При этом заданная скорость отрабатывается системой, как и прежде, без серьезных расхождений, перерегулирование составляет порядка 3 %, что для подъемных механизмов не является существенной погрешностью.

Дальнейшая работа будет направлена на оп- тимизацию модернизированной схемы в рамках повышения устойчивости и нахождения баланса между устойчивостью и энергоэффективностью.

Возможно, этого удастся достичь путем изменения алгебраической составляющей корректирующего блока [13].