Сравнение использования поколенческой стратегии в моделях Голдберга и Холланда при решении однородной минимаксной задачи

Автор: Троцюк Наталья Игоревна, Кобак Валерий Григорьевич

Журнал: Вестник Донского государственного технического университета @vestnik-donstu

Статья в выпуске: 3 (78) т.14, 2014 года.

Бесплатный доступ

Представлен сравнительный анализ эффективности классических моделей Голдберга и Холланда и их модификаций, использующих различные варианты поколенческой стратегии. В классических генетических алгоритмах используется концепция, предполагающая, что количество особей в поколении не изменяется. Рассмотрен подход, позволяющий повысить эффективность работы стандартных моделей Голдберга и Холланда за счёт варьирования количества особей в поколении. Различные варианты поколенческой стратегии применены для решения однородной минимаксной задачи теории расписаний, относящейся к классу NP-полных задач. Проведённый вычислительный эксперимент для различного количества процессоров и работ показал, что данный подход позволяет значительно повысить эффективность работы генетических алгоритмов путём малых изменений стандартных моделей, позволяя получать решение, более близкое к точному.

Еще

Генетические алгоритмы, модель голдберга, модель холланда, np-полные задачи, поколенческая стратегия, теория расписаний

Короткий адрес: https://sciup.org/14250081

IDR: 14250081 | DOI: 10.12737/5708

Текст научной статьи Сравнение использования поколенческой стратегии в моделях Голдберга и Холланда при решении однородной минимаксной задачи

Введение. Теория расписаний — раздел дискретной математики, занимающийся проблемами упорядочения. Существуют различные варианты задач теории расписаний. Часть из них является NP-полными. NP-полные задачи образуют подмножество типовых задач в классе NP, к которым можно свести любую другую задачу из этого класса полиномиально быстрым алгоритмом решения [1, 8, 9]. В различных областях дискретной математики, комбинаторики и логики известно множество задач, принадлежащих к классу NP-полных задач. Для этих задач не найдены полиномиальные алгоритмы. Однако и не доказано, что таких алгоритмов не существует. Нахождение точного решения для задачи из класса NP-полных является практически невыполнимым. Поэтому для таких задач разрабатываются различные методы, позволяющие получить приближённое решение.

Постановка задачи. В данной работе рассмотрена однородная минимаксная задача, которая относится к классу NP-полных задач. Математическая постановка задачи описана в работах [1, 2, 10]. Для её решения существуют различные методы: списочные; точные, основанные на идее метода ветвей и границ; генетические, которые занимают промежуточное место между списочными и точными методами. Получение точного решения возможно только для малого количества заданий и приборов, а при большом количестве использование данного метода крайне затруднительно. Поэтому большое значение приобретает нахождение субоптимальных решений, которые получаются с помощью различных генетических моделей.

Генетические алгоритмы. Для решения поставленной задачи в данной работе подробно рассматриваются модификации моделей Холланда и Голдберга.

Модель Холланда можно отразить в виде последовательности следующих шагов:

Шаг 1. Формируется начальное поколение, состоящее из заданного числа особей.

Шаг 2. Пропорциональный отбор особей и применение генетических алгоритмов (ГА) операторов кроссовера и мутации с заданной вероятностью для создания нового поколения.

Шаг 3. Проверка условия конца работы алгоритма, которая обычно заключается в неизменности лучшего решения в течение заданного числа поколений. Если проверка прошла неуспешно, то происходит переход на шаг 2.

Шаг 4. Лучшая особь выбирается как найденное решение.

Работа выполнена в рамках инициативной НИР.

Модель Голдберга можно отразить в виде последовательности следующих шагов:

Шаг 1. Формируется начальное поколение, состоящее из заданного числа особей.

Шаг 2. Турнирный отбор особей и применение ГА операторов кроссовера и мутации с заданной вероятностью для создания нового поколения.

Шаг 4. Лучшая особь выбирается как найденное решение [3, 5, 6].

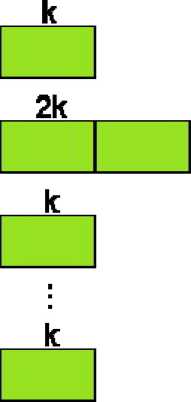
Рис. 1. Схема поколенческой стратегии 1-2

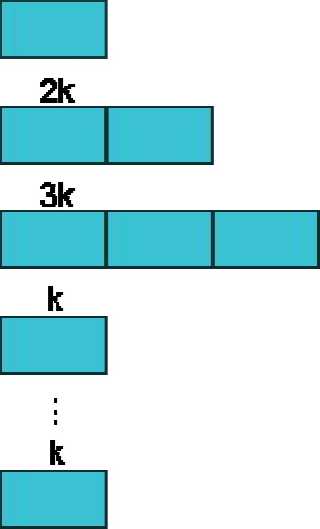
Рис. 2. Схема поколенческой стратегии 1-2-3

Поколенческая стратегия. Из [4, 7] известно, что иногда полезно варьировать размер популяции, то есть количество особей может быть не только постоянным, но и переменным. Применительно к рассматриваемой задаче в модификациях алгоритмов Холланда и Голдберга были использованы базовые изменения количества особей в поколении по следующим схемам:

Схема поколенческой стратегии формирования нового поколения 1-2:

1) В первом поколении задавалось количество особей к.
2) Во втором поколении генерировалось в два раза больше особей, чем в первом поколении.
3) В третьем поколении происходил возврат к исходному количеству особей к.

Процесс продолжался до тех пор, пока значение критерия не повторилось заданное количество раз.

Результаты эксперимента (модификации модели Голдберга)

Таблица 1

N	М	Алгоритм 1		Алгоритм 2		Алгоритм 3		Алгоритм 4		Алгоритм 5
N	М	Ттах среднее	t(c)	Ттах среднее	t(c)	Ттах среднее	t(c)	Ттах среднее	t(c)	Ттах среднее	t(c)
2	23	285,86	0,476	285,43	0,683	285,58	0,898	285,05	1,412	284,95	2,39
	71	873,06	0,567	872,52	0,842	871,97	1,18	871,94	2,013	872,24	3,706
	131	1606,36	0,711	1605,64	1,133	1605,73	1,54	1605,3	2,635	1605,04	5,451
	231	2830,66	1,777	2830,02	3,023	2830,19	4,154	2829,94	7,431	2829,76	16,069
3	23	193,03	0,497	192,89	0,724	192,3	0,967	192,09	1,509	191,92	2,57
	71	586,68	1,473	585,52	2,278	585,23	2,94	584,55	4,528	584,22	8,568
	131	1077,23	1,001	1075,86	1,504	1076,22	2,065	1075,34	3,407	1075,37	6,851
	231	1892,38	1,331	1891,16	2,123	1890,57	3,048	1890,24	5,01	1889,69	10,564
4	23	149,9	0,709	148,02	1,01	147,86	1,245	147,67	2,08	147,99	3,216
	71	446,7	0,928	444,22	1,381	444,2	1,783	443,18	2,872	443,27	5,332
	131	813,72	1,269	813,18	1,914	811,82	2,612	811,9	4,361	811,33	8,362
	231	1426,2	1,775	1425,03	2,618	1424,02	3,649	1423,25	6,481	1422,51	14,043
...
7	23	95,19	0,904	94,41	1,355	94,02	1,686	93,59	2,606	93,45	4,395
	71	266,98	1,375	262,11	2,305	262,5	2,888	260,78	4,823	260,06	8,848
	131	480,13	1,932	475,02	3,107	474,22	4,33	472,83	6,737	470,38	14,266
	231	832,57	2,73	829,73	4,626	825,88	6,227	822,91	11,291	823,92	23,345
11	23	70,88	1,022	69,53	1,58	68,74	2,04	68,1	3,092	66,67	5,836
	71	181,53	1,57	178,74	2,62	177,39	3,237	174,71	5,403	174,51	10,687
	131	322,57	2,223	318,04	3,739	315,67	5,028	313,43	8,591	310,15	18,915
	231	552,27	3,503	545,12	6,524	547,44	7,481	541,91	14,52	536,35	32,471

Схема отражена на рис. 1.

Схема поколенческой стратегии формирования нового поколения 1-2-3 1) В первом поколении задавалось количество особей к.

2) Во втором поколении генерировалось в два раза больше особей, чем в первом поколении.
3) В третьем поколении генерировалось в три раза больше особей, чем в первом поколении.
4) В четвёртом поколении происходил возврат к исходному количеству особей к.

Процесс продолжался до тех пор, пока значение критерия не повторилось заданное количество раз.

Схема отражена на рис. 2.

Кроме того, для модификаций алгоритмов были использованы схемы поколенческой стратегии 1—2—3-4—5 и 1-2-3-4-5-6-7-8-9, которые отличаются от рассмотренных тем, что возврат к исходному количеству особей происходил соответственно после пятикратного и девятикратного увеличения.

Результаты эксперимента (модификации модели Холланда)

Таблица 2

N	М	Алгоритм 6		Алгоритм 7		Алгоритм 8		Алгоритм 9		Алгоритм 10
N	М	Ттах среднее	t(c)	Ттах среднее	t(c)	Ттах среднее	t(c)	Ттах среднее	t(c)	Ттах среднее	t(c)
2	23	286,12	0,223	285,69	0,27	285,02	0,333	284,5	0,492	283,75	0,809
	71	874,49	0,298	873,02	0,393	872,51	0,473	871,89	0,689	871,32	1,086
	131	1609,01	0,387	1606,78	0,515	1606,11	0,652	1605,08	0,907	1604,49	1,5
	231	2834,85	1,198	2831,66	1,48	2831,48	1,727	2829,9	2,527	2828,96	4,034
3	23	195,52	0,234	194,65	0,265	193,46	0,351	192,57	0,523	191,79	0,847
	71	594,81	0,641	591,16	0,903	589,17	1,059	587,64	1,569	585,6	2,513
	131	1077,23	1,001	1075,86	1,504	1076,22	2,065	1075,34	3,407	1075,37	6,851
	231	1910,66	0,747	1907,48	0,957	1904,36	1,213	1898,41	1,635	1894,7	2,674
4	23	155,15	0,269	153,36	0,364	150,66	0,462	150,24	0,657	148,23	1,049
	71	460,63	0,425	457,64	0,509	455,3	0,658	451,46	0,917	447,71	1,495
	131	837,04	0,531	832,02	0,746	829,94	0,825	824,12	1,303	819,47	2,08
	231	1460,77	0,877	1454,65	0,994	1449,31	1,107	1443,37	1,693	1437,93	2,785
...
7	23	104,29	0,308	102,19	0,384	100,49	0,486	98,88	0,685	98,02	1,097
	71	289,77	0,462	287,26	0,62	284,51	0,777	281,57	1,16	277,26	1,781
	131	515,07	0,699	510,98	0,846	507,48	1,075	502,25	1,5	495,49	2,426
	231	883,9	0,83	876,5	1,186	874,28	1,376	868,29	2,098	859,79	3,289
11	23	77,8	0,316	76,86	0,414	75,83	0,511	75,1	0,733	73,6	1,193
	71	206,65	0,493	203,11	0,603	200,5	0,794	198,63	1,186	195,18	1,94
	131	357,08	0,688	355,52	0,982	350,04	1,197	344,9	1,635	342,03	2,861
	231	601,85	1,039	596,8	1,535	594,45	1,739	587,97	2,565	580,22	3,983

В связи с тем, что аналитически доказать, какой из алгоритмов в среднем лучше невозможно, для оценки алгоритмов был проведён вычислительный эксперимент для различного количества приборов. Количество разных матриц для получения средних значений было выбрано рав- ным 100. Диапазон параметров (20-30), который может принимать работа при выполнении на процессоре, является одним из самых используемых. Массив работ генерируется случайно из заданного диапазона. Вероятность кроссовера и вероятность мутации — 1 (то есть происходит всегда). Количество поколений до конца работы алгоритма — 10. Начальный размер популяции — 10. Результаты вычислительного эксперимента приведены в табл. 1, 2, где /V— количество процессоров, М— количество работ, Ттах среднее — среднее значение критерия, t (с) — время работы алгоритма в секундах.

Сравниваемые алгоритмы:

Алгоритм 1 — стандартная модель Голдберга.

тегии

Алгоритм 2 — модификация 1-2.

Алгоритм 3 — модификация 1-2-3.

Алгоритм 4 — модификация 1-2-3-4-5.

Алгоритм 5 — модификация

1-2-3~4-5-б-7-8-9.

модели

тегии

Голдберга, использующая схему

Алгоритм б — стандартная модель Холланда.

Алгоритм 7 — модификация модели Холланда, 1-2.

Алгоритм 8 — модификация модели Холланда, 1-2-3.

Алгоритм 9 — модификация модели Холланда, 1-2-3-4-5.

использующая

поколенческой

стра

схему

Алгоритм 10 — модификация модели Холланда, использующая схему 1-2-3~4-5-б-7-8-9.

поколенческой

стра

Выводы. При увеличении количества процессоров и работ повышение количества особей колении в модификациях моделей Голдберга и Холланда приводит к улучшению результата.

в по-

При сравнительном анализе моделей Холланда и Голдберга (табл. 1, 2) видно, что модификации модели Голдберга дают на 3,5 % результаты лучше, чем модификации модели Холланда, но работают на 76 % дольше.

По сравнению со стандартной моделью, поколенческая стратегия для модели Холланда даёт лучшие результаты, чем для модели Голдберга. Улучшение результатов при использовании поколенческой стратегии для модели Холланда составляет 2,7 %, а для модели Голдберга — 1,5 %. Длительность работы при этом увеличивается на 73 % и на 80,5 % соответственно.

Список литературы Сравнение использования поколенческой стратегии в моделях Голдберга и Холланда при решении однородной минимаксной задачи

Кобак, В. Г. Сравнительные характеристики модификации модели Холланда при поколенческой стратегии/В. Г. Кобак, Н. И. Троцюк, Б. А. Рожковский//Тр. Сев.-Кавк. фил. Моск. техн. ун-та связи и информатики. -Ростов-на-Дону: ПЦ «Университет» Сев.-Кавк. фил. Моск. техн. ун-та связи и информатики, 2014. -Ч. 1. -С. 319-322.
Кобак, В. Г. Сравнительный анализ алгоритмов: генетического с элитой и Крона с генетическим начальным распределением/В. Г. Кобак, Н. И. Троцюк//Мат. методы в технике и технологиях: сб. тр. XXVI междунар. науч. конф. -Саратов, 2013. -Т. 12, ч. 2. -С. 62-64.
Кобак, В. Г. Использование поколенческой стратегии модели Голдберга при решении однородной минимаксной задачи/В. Г. Кобак, Н. И. Троцюк//Аспирант. -2014. -№ 2. -С. 62-64.
Базы данных. Интеллектуальная обработка информации/В. В. Корнеев [и др.]. -Москва: Нолидж, 2000. -352 с.
Нейдорф, Р. А. Сравнительный анализ эффективности вариантов турнирного отбора генетического алгоритма решения однородных распределительных задач/Р. А. Нейдорф, В. Г. Кобак, Д. В. Титов//Вестник Дон. гос. техн. ун-та. -2009. -Т. 9, № 3. -С. 410-418.
Курейчик, В. М. Генетические алгоритмы и их применение/В. М. Курейчик. -Изд. 2-е, доп. -Таганрог: Изд-во Таганрог. радиотехн. ун-та, 2002. -242 с.
Курейчик, В. М. Генетические алгоритмы/В. М. Курейчик, Л. А. Гладков, В. В. Курейчик. -Москва: Физматлит, 2006. -319 с.
Коффман, Э. Г. Теория расписаний и вычислительные машины/Э. Г. Коффман. -Москва: Наука, 1984. -336 с.
Пашкеев, С. Д. Машинные методы оптимизации в технике связи/С. Д. Пашкеев, И. Р. Менязов, В. Д. Могилевский. -Москва: Связь, 1976. -250 c.
Батищев, Д. И. Генетические алгоритмы решения экстремальных задач/Д. И. Батищев. -Воронеж: Воронеж. гос. техн. ун-т, 1995. -69 с.

Еще

Статья научная