Сравнение изображений на основе их диффеоморфного преобразования
Автор: Лейхтер Сергей Владимирович, Чуканов Сергей Николаевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Обработка изображений, распознавание образов
Статья в выпуске: 1 т.42, 2018 года.
Бесплатный доступ
Рассмотрена задача сравнения двух диффеоморфных изображений - начального изображения диффеоморфизма и конечного изображения диффеоморфизма, которые задаются множеством точек. Задача решается на основе метода построения минимизируемого функционала, характеризующего эволюцию диффеоморфного преобразования изображения от начального до конечного, и штрафа за отклонение траектории изображения от требуемой траектории. Разработан итерационный алгоритм решения уравнения диффеоморфного преобразования на основе итеративного метода решения уравнений. Рассмотрена задача сравнения двух изображений с использованием построения функционала при оптимальном метаморфозисе изображений.
Распознавание образов, обучение, уравнение эйлера-пуанкаре, диффеоморфные преобразования, метаморфозис
Короткий адрес: https://sciup.org/140228714
IDR: 140228714 | DOI: 10.18287/2412-6179-2018-42-1-96-104
Текст научной статьи Сравнение изображений на основе их диффеоморфного преобразования
В работе рассматривается проблема сравнения двух диффеоморфных изображений – начального (до операции диффеоморфного преобразования) и конечного (после операции диффеоморфного преобразования). Изображения представляют собой кривые, которые определяются множеством точек. Предлагается метод построения минимизируемого функционала, который характеризует эволюцию диффеоморфного преобразования изображения от начального до конечного, и штрафа за отклонение траектории изображения от требуемой. Задача приводится к системе обыкновенных дифференциальных уравнений первого порядка Эйлера–Пуанкаре путём использования вариационного исчисления. Разработан алгоритм решения задачи диффеоморфного преобразования на основе метода обучения. Задача сравнения двух изображений может быть использована при оптимальном метаморфозисе изображений, когда отсутствует точное соответствие между целевым изображением и конечным изображением диффеоморфизма. Разработанные алгоритмы могут быть использованы в биоинформатике и биометрических системах, при классификации изображений и объектов, в системах машинного зрения, при распознавании изображений, в системах слежения.
являются диффеоморфными ( M ~ N). Группа диффеоморфизмов дифференцируемого многообразия M – это группа всех диффеоморфизмов M→M, обозначаемая Diff(M).
Для определения расстояния между элементами множества X (например, точками, кривыми, изображениями и т.д.) ввёдем понятие метрического пространства. Непустое множество элементов X с неотрицательной метрикой d ( x , y ) ∈ R ; x , y ∈ X называется метрическим пространством, если d обладает свойствами: симметрии: d ( x , y ) = d ( y , x ); неравенства треугольника: d ( x , y ) ≤ d ( x , z ) + d ( z , y ); { d ( x , y ) = 0} ↔ { x = y }; ∀ x , y , z ∈ X .
Если два объекта заданы множествами точек x i , y i ; i = 1, ..., N , то для формирования метрического пространства можно использовать евклидову метрику L 2:
( N
d=|Ё (x
V i =1
-
y i ) 2
0,5
Существует бесконечное множество траекторий диффеоморфизмов x i → y i , поэтому необходимо выбрать характеристику каждой траектории и минимизировать эту характеристику. Пример задачи Снел-лиуса о преломлении луча света на границе двух сред показывает, что евклидово расстояние между источником и приемником луча не соответствует принципу наименьшего действия.
Диффеоморфное отображение изображений (визуализируемых объектов): n0 → n1, где n0 – исходный шаблон изображения и n1 – целевое изображение, может быть представлено траекторией диффеоморфизмов gt = g (t); t∈[0, ..., 1], в которой g (0) =Id и ni = g(1)оn0. Группа диффеоморфизмов состоит из элементов gt ∈ G =Diff(M), которые порождают орбиты изображений M ={g ⋅ n | g∈G}; эти орбиты можно рассматривать как гладкое риманово многообразие, так как для любого n∈M существует скалярное произведение, индуцирующее норму. Это, в свою оче- редь, порождает рассмотрение группы диффеоморфизмов G =Diff(M) как риманова многообразия.
В методе LDDMM ( large deformation diffeomorphic metric mapping ) [1, 2, 3] в качестве метрики применен минимум длины траектории преобразований в пространстве диффеоморфизмов. Для этого авторы определяют лагранжиан, интеграл которого на траектории этого отображения (действие) должен быть минимальным.
Пусть M – дифференцируемое многообразие визуализируемых объектов, на котором действует лиева группа диффеоморфизмов G =Diff(M) с алгеброй g . Предположим, что g – гильбертово пространство с нормой || ⋅ || g . Риманова метрика может быть определена из скалярного произведения векторных полей < v,w V ( L g v,w ) L 2 ; v,w eg; L g v eg * , где L g — линейный обратимый оператор.
Назовем метаморфозисом ( metamorphosis ) [4] – бинарную дифференцируемую операцию, которая преобразовывает начальное изображение (шаблон) в конечное (целевое) изображение с получением множества промежуточных форм. Рассмотрим операцию метаморфозиса для пары визуализируемых объектов [3, Notation 1]: ( gt , η t ) ∈ G × M, параметризованную t ∈ [0, ..., 1]. gt является деформацией – элементом группы диффеоморфизмов gt ∈ G , g 0 =id. Будем использовать символы η t , nt ∈ M, где nt = gt ⋅ η t ∈ M ассоциируется с эволюцией изображения объекта: в случае η t = const – метаморфозис является диффеоморфизмом; η t – остаточная часть метаморфозиса, которая не может быть представлена диффеоморфной эволюцией изображения.
В случае метаморфозиса для пары визуализируемых объектов оценка динамики изменения изображения и векторного поля скоростей декомпозируется в диффеоморфное отображение и остаточную часть ме-таморфозиса. Метаморфозис позволяет разрешить нарушение диффеоморфного ограничения: соответствие в топологии между шаблоном и целевым изображением. При этом точное диффеоморфное сопоставление между шаблоном и целевым изображением заменяется неточным механизмом эволюции изображения. Выбор остаточной части метаморфозиса не является однозначным, и задача относится к некорректным, для которой применяется метод регуляризации.
Следует отличать операцию метаморфозиса от технологии морфинга, который получается преобразованием одного изображения в другое посредством плавного перехода. Морфинг, например, используется в программном продукте Adobe After Effects CC. Морфинг не позволяет декомпозировать преобразование изображений объектов на диффеоморфное преобразование и остаточную часть преобразования и требует соответствия в топологии между шаблоном и целевым изображением.
Для иллюстрации операции метаморфозиса рассмотрим отображение трех точек n 0 = η 0 → n 1 на плоскости R 2:
n 0 =
n1 =
X °
V
x; y
V
x 2 0 y 2 0 1
x 1 2 y 12 1
X 3 y
1 .
x 3
y 3
1 .
Г - 1 0 1 0
Г 0 10 0
-1
1 17
Предположим диффеоморфизм ограничен группой SE (2) с элементами:
Г Rt T 0
g t V 0 1 ,
где Rt ∈ SO (2) – элемент группы вращения на плоскости, Tt ∈ R 2 – элемент группы переноса на плоскости. Очевидно, что невозможно подобрать такой g 10 ∈ SE (2), который обеспечит точное равенство n 1 = g 10 ⋅ n 0. Можно сформировать такое неточное отображение: nt = gt ⋅ η t , что n 0 = g 0 ⋅ η 0 , g 0 =Id и n 1 ≈ g 1 ⋅ η 1 , где η t , t ∈ [0, ..., 1] – шаблон, который является остаточной частью мета-морфозиса.
Выбор остаточной части метаморфозиса η t не является однозначным, то есть задача относится к некорректным. Для решения некорректных задач применяется метод регуляризации: минимизируется функционал:
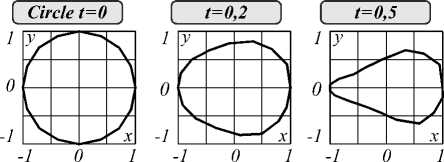
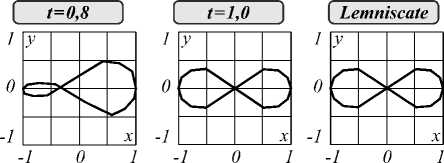
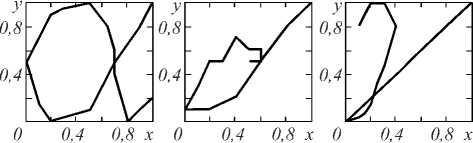
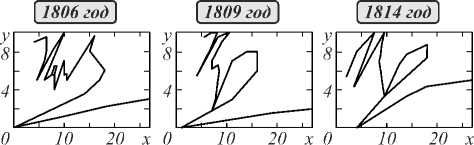
5=j(Ii“tiig+°-2nt—u>n>\2)dt, ut= на траектории с условиями nt=0= n0= η0 и nt=1 = n1; здесь σ –2 – коэффициент регуляризации. Отметим, что при отсутствии учёта диффеоморфизма (ut = gɺ t gt-1= 0,∀t) функционал приводится к виду: S = Jnt |2dt; g = 1. 2. Уравнение Эйлера–Пуанкаре Для сравнения двух изображений найдем оптимальную деформацию, которая переводит одно изображение в другое. Для этого сформируем минимизируемый функционал [5, глава 11]: J L (g ’ 8J 1 (и, n, v)d t = 0, для элементов группы диффеоморфизмов g е G = Diff(M). Из условия оптимизации действия: S = J 1 (u, n, v) d t 0 по отношению к вариации 8и и ю = 8n = 8(gп) при фиксированных n0, n 1, определим уравнения Эйлера-Пуанкаре. Найдем производную по времени ю: ю = 8v + ию+8un. Вариационное условие оптимизации: 8S = 0 приводит к соотношению: ю - ию-(8и)n) I dt = 0, откуда можно получить систему уравнений [8]: 81 81 д п — + — ◊ n = 0, 8 и 8v 81 81 + и *---= 0 , 8v 8 n А (81) dtV8v J здесь оператор ◊ определяется из соотношения: {v◊ a, £) = {a, £v), V^e,; оператор * определяется из соотношения: 81 и * —, ю 8v , Для построения полной системы уравнений добавим соотношение для эволюции изображения при мета-морфозисе: n = v + un . Элементы группы диффеоморфизмов g(x)е G; xeM могут быть представлены в форме потоков обыкновенных дифференциальных уравнений, которые эволюционируют во времени t е [0,1] с векторным полем скоростей и (•) [8]: dg (x) dt = и ° g (x); gt=0(x) = x. Запишем скалярное произведение в пространстве g в форме, соответствующей метрике С.Л. Соболева: (и, v) = /Lи,v\ = f(Lи) vdx; xe M; ' ' g \ g / l2 J v g / M II и11, = ^ и,“^ g, где Lg - линейный оператор, отображающий элементы лиевой алгебры g на элементы лиевой коалгебры g*: Lg: g^g*. В случае механической интерпретации величина L,и имеет смысл вектора импульса, и - вектора скорости, а L, - тензора инерции. Наличие нормы ||- ||, в пространстве g позволяет считать это пространство метрическим. Введём обратный оператор K, которой формально представим в виде: K = L,1. Для элементов группы gtе G; tе [0,..., 1] существуют скорости изменения gt: и = (dgt/dt)gt-1Eg, которые минимизируют функционал: S = J1 (и, v) dt с лагранжианом: 1 (и,v) = ||и|I, + o-2 |v|2, (5) где в соответствии с (4): v = n - un, на траектории, соединяющей элементы группы g0 = g|t=0, g 1= g11 =1; здесь первое слагаемое ||и||, соответствует энергии регуляризации диффеоморфизма, аналогичное регуляризации А.Н. Тихонова при решении некорректных задач; второе слагаемое о-2|v|2 накладывает штраф за отклонение | v | = | n - un |, обратно пропорциональный величине о2. Выражение для импульса можно формально записать в виде p = Lgи; тогда обратное выражение: и = L,1p = Kp, которое представим с использованием аппроксимирующей скалярной функции K (x, у): и (x ) = J K (x, у) p (у) dу . Q Для оператора: Lg=id- aV2 в пространстве R2 -обратным оператором формально является оператор: K = L-1, который можно аппроксимировать скалярной функцией Гаусса [9]: -11 |2 3. Метаморфозис точечных множеств K (x, у ) = вe~к |x-y . (6) Уравнения эволюции диффеоморфизмов Эйлера-Пуанкаре можно получить решением уравнений вариационной задачи с лагранжианом (5) [10]: .? = и (g), и = L,-1 p = Kp, (7) p = - (Dp) и - p V и - ( Du ) T p, где Df = |fi- . dx, V j 7 Пусть заданы два множества n0 = (x 1,..., xN), n 1 = (уi,...,yN) помеченных точек в M. Поставим задачу нахождения такого минимального диффеоморфизма: g:M^M, что g(xi)~у,; i =1,...,N (неточное соответствие). Множество диффеоморфизмов Diff(M) определяют структуру группы. Для точечных множеств можно записать: N p (у ) = Е pi '8( у- qi^, (8) i=1 откуда получим: и (x ) = Ек (x, qi) p,. (9) i =1 Пусть пространство M содержит N объектов (точек), которые подлежат деформации. Рассмотрим действие 5 с лагранжианом: N l(u,v) = |u|g +о-£|vJ . (10) к=1 Из уравнений (2, 4, 7) и обозначения n = (qb..., qN) получим соотношение для точечных множеств в виде (см. Приложение 1): q к = u (qk) + о2 рк; к = 1,.., N, u (q) = ^^K (q, <к) Pk, (11) к =1 Р к+NNV1K(qk, ql) PTPi = 0, l=1 где Pk = о 'vк. В работе [11] приводится метод построения лагранжиана для случая диффеоморфного отображения точечных множеств, но не учитывается штраф за отклонение от целевой траектории ~| v |. Использование неточного метаморфозиса в (11) позволяет отображать исходные изображения в целевые даже в случае несовпадения их топологий. Для системы дифференциальных уравнений: x (t) = u (t, x(t)), где u (t, x) - функция непрерывная по t и равномерно непрерывная по Липшицу по x с условием x(t0)= x1t=10=x0, существует непрерывно дифференцируемое решение: x(t)= у(t, t0,x0) на интервале tе[t0-е, t0 + е] для некоторого е >0. Правые части дифференциальных уравнений (11) являются непрерывно дифференцируемыми по аргументам (qk,рк); к =1,...,N, поэтому решения (11), рассматриваемые как функции (qk,Рк)(t)= у(t0,qk1t=t0,Рк1t=t0), будут непрерывно дифференцируемыми по аргументам (t0, qk11=10,Рк11=10); к = 1,..., N. Рассмотрим метод обучения в задаче нахождения метаморфозиса qk(0) ^ qk(1) при минимизации функционала N 2 j = N [q , (t) - q , (1)] ^ min, i=1 где q(target) = (q1(t),.., qN(t)) - целевое множество точек. Так как для системы дифференциальных уравнений (11) для вектора q заданы начальные условия q(0) при t = 0, а для вектора Р - терминальные: р(1) = (0, ...,0) при t =1, то получаем двухточечную краевую задачу. Сведение этой задачи к задаче Коши может быть проведено различными способами: стрельбы, квазилинеаризации, инвариантного погружения и т.д. Найдем требуемый вектор начальных значений: р(0) = (р 1(0),...,pN(0)) с помощью итерационного метода определения начальных условий для системы дифференциальных уравнений (11): рк+1 (0)=рк (0)+^ , др (0) где р - коэффициент обучения; d J д J д J др (0) дР1 (0), , дPn (0) - градиент функционала по вектору р(0); к - номер итерации. Для нахождения компонент градиента дJ др,. (0) (J + 5J)-J lim -----——, i = 1, 5р,(0)^0 5pi (0) ,N определяется функционал J численным решением системы дифференциальных уравнений (11) с вектором начальных условий р(0) = (р 1(0),...,pN(0)) и функционал J + 5J численным решением системы дифференциальных уравнений (11) с вектором начальных условий: Р(0) = (Р1 (0) ’••’ Р,-1 (0), Р, (0) + 5Р,, Р+1 (0) ’••’ Pn (0)) ■ Пример 1. Рассмотрим пример метаморфозиса окружности (число топологических ручек - 1) в лемнискату Бернулли (число топологических ручек - 2), которые задаются 16 точками, расположенными на кривых, на основе интегрирования дифференциальных уравнений (11), полученных вариационным методом из лагранжиана (8). Точки расположены в пределах квадрата 0< xh yt<1; i =1,..., 16. На рис. 1 приведены промежуточные изображения при метаморфозисе окружности в лемнискату Бернулли. Рис. 1. Метаморфозис окружности в лемнискату Бернулли В табл. 1 приведены значения функционала 5 = j l (u, v) d t 0 с лагранжианом (8) в зависимости от о2. Табл. 1. Значения функционала S с лагранжианом (8) о2 = 0,1 о2 = 1 о2=10 1 5=jl Н12dt 0 33,0 18,4 1,9 Пример 2. Рассмотрим пример нахождения деформации на основе интегрирования дифференциальных уравнений (11) при метаморфозисе греческих строчных символов а, 5, у, р, о, которые представлены 16 точками, равномерно расположенными на кривой символов; точки расположены в пределах квадрата 0 ≤ xi, yi ≤ 1; i = 1, ..., 16. Интегрирование уравнений проводилось при α = 10; µ = 0,1. Минимизируемый функционал определяется на основе соотношения: S = Jl (u, v) dt с лагранжианом (8) и σ2 = 10. Табл. 2. Результаты расчета функционала S при метаморфозисе греческих строчных символов α, δ, γ, ρ, σ α δ γ ρ σ α 0 31,9 28,6 37,4 26,2 δ 31,4 0 21,6 39,1 14,9 γ 26,3 21,9 0 46,7 15,2 ρ 38,2 38,9 46,8 0 44,3 σ 26,1 15,0 14,9 44,5 0 Из табл. 2 следует, что наименьшего значения функционала требуют метаморфозисы σ ⇔ δ и σ ⇔ γ; наибольшего значения функционала требуют метамор-фозисы ρ ⇔ σ и ρ ⇔ γ. Метаморфозис a ^ Y в различные моменты времени представлен на рис. 2, на котором приведены промежуточные изображения при метаморфозисе символа α в символ γ. | t=0 ] 11=0,5 ] | t=l,0 ] Рис. 2. Метаморфозис символа α в символ γ Рассмотрим случай, когда M – пространство гладких функций (изображений) Ω → R с действием (g, n) → n·g–1. Будем обозначать координаты элемента изображения символом q∈Ω∈Rd (в случае плоских изображений d = 2). Для случая метаморфозиса изображений с действием S и лагранжианом: l(u,ν) = u 2g + σ-2 ν2 перепишем уравнения эволюции (2, 7) в виде (Приложение 2): zɺ + ∇ ( zu ) = 0, nɺ + (∇nT ) ⋅ u = σ2z, (12) Lgu + z∇n = 0. где z = σ –2v. Для дискретного двухмерного случая будем считать qij = (xi, yj)T; ∆ = ∆x = ∆y; dq = ∆2. Запишем выражение для u в виде: u (q) = -J K (q, q) z (q)V n (q) d q " Ω "-ibtK (q, ij) z (qj) V n (ij )A2; (13) ji q, qɶij ∈ Ω∈ R2. Оператор K = Lg-1 аппроксимируем скалярной функцией Гаусса: K(q1,q2)=βe-α-1q1-q22=βe-α-1(x1-x22+y1-y2 Рассмотрим метод обучения в задаче нахождения метаморфозиса n(0) → n(1) при минимизации функционала NN 2 J‘=bbl n(qij,target)-n(qij,1) I ^ min, j=1 i=1 где n(1) – конечное изображение при t = 1, n(target) – целевое изображение. Так как для системы дифференциальных уравнений (12) для изображения n заданы начальные условия n (0) при t =0, а для вектора z – конечные: z (1) = (0, ..., 0) при t = 1, то получаем двухточечную краевую задачу. Найдем требуемый вектор начальных значений: z(0) = (z1(0), ..., zN(0)) с помощью итерационного метода определения начальных условий для системы дифференциальных уравнений (12): zk+1(0)=zk(0)+µ⋅∂z∂J(0′), где µ – коэффициент обучения; dj ' = dj ' dj ' dz (0) dzi (0) , , dzN (0) – градиент функционала по вектору z(0); k – номер итерации. Компоненты градиента (∂J ′/∂z(0)) определяются аналогично нахождению компонент градиента (∂J/∂p(0)) для изображений, которые представлены множеством точек. Пример 3. Рассмотрим пример метаморфозисов арабских цифр при: σ2= 10; β = 0,1; α = 10; N = 11; µ = 0,1. Результаты расчёта функционала диффеоморфизмов приведены в табл. 3. Табл. 3. Результаты расчёта функционала J || u ||^ dt при метаморфозисе арабских цифр 0 1 2 3 4 0 0 0,1899 0,1689 0,0347 0,1963 1 0,3477 0 0,3375 0,3287 0,1606 2 0,3299 0,1587 0 0,2486 0,2062 3 0,0406 0,1884 0,2524 0 0,2046 4 0,3695 0,2934 0,4091 0,2044 0 Метаморфозис 1 → 9 в различные моменты времени представлен на рис. 3. В данном случае непрерывная дифференцируемость может быть нарушена в ус- ловиях моделирования на цифровых вычислительных машинах. Рис. 3. Метаморфозис цифры 1 в цифру 9 В настоящее время в вычислительной анатомии (computational anatomy) широко применяется метод LDDMM (large deformation diffeomorphic metric mapping) (см. статьи [2, 3, 12, 13], а также монографии [14, 15]). LDDMM представляет набор алгоритмов, используемых для отображений и операций с деформируемыми изображениями, основанными на диффе-оморфном метрическом отображении. В биометрии [16] используются метрические пространства параметров (биометрических идентификаторов), связанных с характеристиками человека. Примерами биометрических идентификаторов могут быть: отпечатки пальцев, рисунки вен ладони, распознавание геометрии формы рук и лиц, распознавание сетчатки глаз, нахождение соответствия подписей и т.д. К биометрическим характеристикам поведения человека можно отнести походку, почерк, динамику написания текста и нажатия клавиш клавиатуры, формирования подписи. Использование методов ме-таморфозиса расширяет возможности распознавания образов в задачах биометрии. Рассмотрим пример применения метода метамор-фозиса для определения метрики подписей Наполеона, сделанных им в различные годы: 1806 в Берлине, 1809 в Шёнбруне, 1814 в Фонтенбло. Пример 4. На рис. 4 представлены образцы подписи Наполеона, сделанные им в 1806, 1809 и 1814 годах. Образцы подписи аппроксимированы отрезками прямых. Рис. 4. Образцы подписи Наполеона В табл. 4 представлены результаты определения функционала S = J1 (u, v) dt с лагранжианом (8) для отображений подписей. Если ввести метрические расстояния между кривыми d = S с лагранжианом (8), то из табл. 4 следует, что d (1806, 1814) > d (1806, 1809) и d (1809, 1814) > d (1806, 1809), то есть подпись 1809 года имеет большее сходство с подписью 1814 года, чем с подписью 1806 года. Табл. 4. Результаты определения функционала S с лагранжианом (8) для отображений подписей 1806 год 1809 год 1814 год 1806 год 0 1518 1578 1809 год 1429 0 643 1814 год 1600 735 0 Заключение В работе рассмотрена задача сравнения двух диф-феоморфных изображений – начального изображения и конечного (целевого) изображения. Задача решается на основе метода построения минимизируемого функционала, характеризующего эволюцию диффеоморф-ного преобразования изображения от начального до конечного, и штрафа за отклонение траектории изображения от требуемой траектории. Разработан алгоритм решения уравнения диффеоморфного преобразования на основе метода обучения. Рассмотренная задача сравнения двух изображений может быть использована при оптимальном ме-таморфозисе изображений. При этом эволюция изображения от исходного шаблона до целевого изображения декомпозируется на эволюцию, обусловленную диффеоморфным отображением, и остаточные деформации метаморфозиса. Методы метаморфозиса могут быть использованы в случаях, когда отсутствует точное соответствие между целевым изображением и конечным изображением диффеоморфизма или когда топологии исходного шаблона и целевого изображения различны. Приложение 1. Вывод уравнений Эйлера–Пуанкаре для случая точечных множеств Для заданных двух множеств n0 = (x1, ..., xN), n1 = (y1, ..., yN) помеченных точек в M поставим задачу нахождения такого минимального диффеоморфизма (см. параграф 3): g: M ^ M, что g (xi) ~ yi; i =1,..., N (неточное соответствие). Для точечных множеств: N p (y )=E Pi-§( y- q-^, i=1 получим: U (X ) = Ek (X, q) pi. i=1 Рассмотрим действие: S = J1 (u, v) dt с лагранжианом [8]: N 1(u,v) = ||u|Ig IG2Elvt| = k=1 N =1 lulL+a-2 El‘ik-u (qk )|, k=1 который не зависит от n. Тогда: 51 51 — = 2L„u , — = 2g2 v.,.., v„ . 5 u g , 5v ( 1, ’ N) Из уравнения (2) имеем: lgu=о-2ivk -§( q-qk), k=1 откуда: u(q) = £k(q,qk) Pk, (9) k=1 где pk = о -2vk. Из соотношений (2, 7) получим: pk+Du (qk) T Pk = N (11.3) = pk+i vi K (qk, qi) pTPi = 0; k = и, N, i=1 где V!K представляет собой градиент функции (qk, ql) ^ K(qk, ql) по отношению к qk. Если для оператора Lg выбрать функцию Грина в виде: -11 12 K(qk,q, ) = ₽e~к qk-ql' , -1|„ I2 то V1K(qk,Qi) 2aЩqk-Qi)e k ll . Из уравнения эволюции метаморфозиса (4) и обозначения n = (q1, ..., qN) получим соотношение: qk =vk+ u(qk) = u(qk)+°2Pk; k = 1,••,N, которое при о2 ^ 0 соответствует (7.1). Перепишем систему (7) с учётом (4) для точечных множеств в виде, соответствующем соотношению (11) параграфа 3: qk = u (qk ) + о2Pk; k = 1,.., N, u (q ) = ук (q.qk) Pk, (11) k=1 Pk + i V,K (qk,qi) PT Pi = 0. l =1 Приложение 2. Вывод уравнений Эйлера–Пуанкаре для случая изображений В случае, когда M – пространство гладких функций (изображений) W ^ R с действием (g, n) ^ n ◦ g-1, обозначим координаты элемента изображения символом qeQeRd (для плоских изображений d = 2). Простой случай метаморфозиса можно получить с помощью действия: S = Jl (u, v) dt с лагранжианом [8]: l(u,v) = ||u||2 + o 2|v|2. Если w является элементом лиевой алгебры wе g, а n – изображение объекта, которое представлено гладкими функциями, то действие элемента лиевой алгебры на функцию изображения объекта может быть представлено в виде: wn = -VnTw; следовательно (с учётом определения оператора ◊ в соотношении (2)): 8ч — ◊ n 8 v w f 81 ^ 8 v V nTw Так как (81/ 8v) = 2о 2v, то из соотношения (2) получим: Lgu + zVv = 0, где z = о -2v. Так как u * (81/8v) в соотношении (3) определяется формулой: (см. пара- то из (3) получим уравнение: .z + V ()zu = 0 . Перепишем уравнения эволюции (2) и (7) для случая метаморфозиса изображений в виде граф 5): .z + V( zu) = 0,ni + (VnT) • u = о2 z,Lg u + z V n = 0. Из последнего соотношения получим: u (q) = -Lg1 (z V n) = -K (z V n) == -J K (q_, q) z (q )V n (q) dq; q, q eQ. Q Для дискретного двухмерного случая будем считать qij = (Xi, yj) T; A = Ax = Ay; dq = А2. Запишем выражение для u в виде: u (q) = -J k (q, qf) z (qf) v n (-?) d = Q NN “ iiK(q,qi/)z(qlд') Vn(j)A2; q,qly eQe R2. ji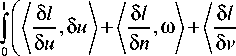
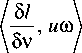
4. Обучение начальных значений
5. Метаморфозис изображений

6. Использование метода метаморфозиса в задачах биометрии
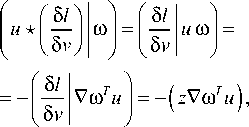
Список литературы Сравнение изображений на основе их диффеоморфного преобразования
- Beg, M. Computing large deformation metric mappings via geodesic flows of diffeomorphisms/M. Beg, M. Miller, A. Trouvé, L. Younes//International Journal of Computer Vision. -2005. -Vol. 61, Issue 2. -P. 139-157. - DOI: 10.1023/B:VISI.0000043755.93987.aa
- Miller, M. Group actions, homeomorphisms, and matching: a general framework/M. Miller, L. Younes//International Journal of Computer Vision. -2001. -Vol. 41, Issue(1-2). -P. 61-84. - DOI: 10.1023/A:1011161132514
- Trouvé, A. Metamorphoses through lie group action/A. Trouvé, L. Younes//Foundations of Computational Mathematics. -2005. -Vol. 5, Issue 2. -P. 173-198. - DOI: 10.1007/s10208-004-0128-z
- Долговесов, Б.С. Функции возмущения в геометрическом моделировании/Б.С. Долговесов, С.И. Вяткин//Программные продукты и системы. -2009. -№ 4. -С. 117-120.
- Holm, D.D. Geometric mechanics and symmetry: from finite to infinite dimensions/D.D. Holm, T. Schmah, C. Stoica. -Oxford: Oxford University Press, 2009. -537 p. -ISBN: 978-0-19-921290-3.
- Chukanov, S.N. Definitions of invariants for n-dimensional traced vector fields of dynamic systems//Pattern Recognition and Image Analysis. -2009. -Vol. 19, Issue 2. -P. 303-305. - DOI: 10.1134/S105466180902014X
- Чуканов, С.Н. Формирование инвариантов при визуализации векторных полей на основе построения оператора гомотопии/С.Н. Чуканов, Д.В. Ульянов//Компьютерная оптика. -2012. -Т. 36, № 4. -С. 622-626.
- Holm, D.D. The Euler-Poincaré theory of metamorphosis/D.D. Holm, A. Trouvé, L. Younes//Quarterly of Applied Mathematics. -2009. -Vol. 67, Issue 4. -P. 661-685. - DOI: 10.1090/S0033-569X-09-01134-2
- Younes, L. Evolutions equations in computational anatomy/L. Younes, F. Arrate, M.I. Miller//NeuroImage. -2009. -Vol. 45, Issue 1. -P. S40-S50. - DOI: 10.1016/j.neuroimage.2008.10.050
- Arnold, V. Sur la géométrie différentielle des groupes de Lie de dimension infinie et ses applications à l'hydrodynamique des fluides parfaits/V. Arnold//Annales de l'institut Fourier. -1966. -Vol. 16, Issue 1. -P. 319-361. - DOI: 10.5802/aif.233
- Camassa, R. A geodesic landmark shooting algorithm for template matching and its applications/R. Camassa, D. Kuang, L. Lee//SIAM Journal on Imaging Sciences. -2017. -Vol. 10, Issue 1. -P. 303-334. - DOI: 10.1137/15M104373X
- Glaunès, J. Large deformation diffeomorphic metric curve mapping/J. Glaunès, A. Qiu, M. Miller, L. Younes//International Journal of Computer Vision. -2008. -Vol. 80, Issue 3. -P. 317-336. - DOI: 10.1007/s11263-008-0141-9
- Joshi, S. Landmark matching via large deformation diffeomorphisms/S. Joshi, M. Miller//IEEE Transactions on Image Processing. -2000. -Vol. 9, Issue 8. -P. 1357-1370. - DOI: 10.1109/83.855431
- Grenander, U. Pattern theory: from representation to inference/U. Grenander, M. Miller. -Oxford University Press, 2007. -596 p. -ISBN: 978-0-19-929706-1.
- Younes, L. Shapes and diffeomorphisms/L. Younes. -Berlin, Heidelberg: Springer Science & Business Media, 2010. -434 p. -ISBN: 978-3-642-12054-1.
- Encyclopedia of biometrics/ed. by S.Z. Li, A. Jain. -New York: Springer Publishing Company, Inc., 2015. -1626 p. -ISBN: 978-1-4899-7487-7.


