Сравнение изображений по форме с использованием диффузной морфологии и диффузной корреляции

Задача сравнения изображений по форме безотносительно к яркостной составляющей их пикселей часто возникает на практике, например, в случае сравнения изображений, полученных при различных погодных условиях, условиях освещённости, в разное время суток, в различных спектральных диапазонах и т.д.

Наиболее популярный в настоящее время метод сравнения форм изображений использует меру взаимной информации, вычисляемую по эмпирическому совместному распределению яркостей двух изображений [1]. Однако такой подход исходит из статистических соображений и не рассматривает понятие формы изображения в явном виде. В то же время широко известен и другой подход, предложенный Ю.П. Пытьевым – морфологический анализ изображений (морфология Пытьева), основанный на геометрическом и алгебраическом описании формы [2]. Этот подход выражает геометрическую идею о форме изображения в явной форме и предлагает базовый метод сравнения изображения с формой другого изображения посредством морфологического коэффициента корреляции. Кроме того, в рамках данного направления был разработан целый ряд различных морфологических средств анализа и сравнения изображений. В частности, в статье [3] с помощью данного подхода был предложен коэффициент геометрической корреляции мозаичных форм изображений, оцениваемый как среднеквадратичный коэффициент морфологической корреляции (СКМК).

К сожалению, эксперименты по взаимной привязке ТВ- и ИК-изображений показали, что все эти методы сравнения изображений по форме недостаточно устойчивы по отношению к шуму и высокочастотным искажениям. Более того, качество результатов привязки во многом зависит от качества предварительной сегментации изображений, поскольку форма мозаичных изображений традиционно описывается как набор однородных областей разбиения кадра, вследствие чего она чрезвычайно чувствительна к шуму, применяемому алгоритму сегментации и его параметрам.

Между тем в области алгоритмов снижения размерности и сравнения данных известны устойчивые методы, основанные на тепловых ядрах и диффузных операторах [5]–[8]. Их применение не требует предварительной сегментации данных, и это позволяет надеяться, что возможные модификации морфологических методов, основанные на таких диффузных операторах, будут более робастны.

В данной статье предлагается обобщение морфологического анализа изображений Пытьева, основанное на тепловых ядрах и диффузных операторах. В рамках диффузной морфологии сравнение изображений по форме осуществляется с использованием диффузной корреляции, являющейся непосредственным обобщением Пытьевской морфологической корреляции. Для проверки практической полезности предлагаемого подхода поводится экспериментальное сравнение диффузной корреляции со взаимной информацией, морфологической корреляцией и геометрической корреляцией (СКМК) на примере задачи взаимной привязки ТВ- и ИК-изображений одной сцены.

1. Обзор существующих подходов Взаимная информация

Взаимная информация является статистической мерой, которая определяет количество информации, содержащееся в одной случайной величине, о другой. Она определяется как расстояние Кульбака–Лейблера между эмпирическим совместным вероятностным распределением двух случайных величин и оценкой такого распределения для случая их полной статистической независимости:

I (A, B ) = H (A) + H (B)-H (A, B), (1)

H ( A ) = -S Pa ( a ) log Pa ( a ), H ( B ) =

a

= -S Pb (b ) log Pb (b ) ’

b

H(A’B) = SSPab (a’b) logPab (a,b)’ ab где H(A) – энтропия A, H(B) – энтропия B, H(A,B) – совместная энтропия A и B. В случае сравнения формы изображений для двух значений интенсивностей a и b пары соответствующих пикселей на двух изображениях эмпирические оценки совместного и частных распределений формируются посредством расчёта нормализованных совместной (2D) и частных (1D) гистограмм. За последние годы был создан ряд успешных приложений данного метода сравнения изображений по форме [8], [9].

Морфологический анализ изображений и геометрическая корреляция

В рамках простейшей морфологии Пытьева [2] изображения рассматриваются как кусочно-постоянные функции вида

n f (x, y )=S ft x Fi (x, y), i =1

где n - число областей разбиения F кадра Q на связные непересекающиеся области постоянной яркости F = { F 1 ,…, F n }; f = ( f 1 ,…, f n ) – вектор действительных значений яркости, соответствующих каждой области разбиения; x Fi ( x,y ) e {0,1}— характеристическая функция i -й области яркости:

X f , ( x , У ) =

1,

0,

если (x, y) e Ft в противном случае.

(3) может

Множество изображений одной формы разбиения кадра F в таком случае образовывает выпуклое и замкнутое подпространство F c L 2 ( Q ):

F = {f (x, У ) = S fi X F (x, У), f = {f.....fn},f e Rn}.

Для любого изображения g ( x , y ) e L 2 ( Q ) быть определена проекция на форму F :

g F ( x , y ) = P F g ( x , У ) = ^Lg F X F i ( x , у ) , i =1

gF. = ( ^X F’ g V||^X X i = 1’.’ n •

Морфологическое сравнение изображений f ( x,y ) и g ( x, y ) в рамках морфологии Пытьева может осуществляться с помощью нормированных морфологических коэффициентов корреляции Пытьева:

K m ( g , F ) = '' g ’ K m ( f , G ) = IL P i f ll.

|| g ||                                  || f ||

Здесь в первом случае изображение g сравнивается с формой изображения f, а во втором случае, на- оборот, изображение f сравнивается с формой изображения g.

Для того чтобы не учитывать постоянную неинформативную часть яркости изображения, производится нормализация с использованием проекций:

K m ( g , F ) =

II P F g — P_Og ll

II g — P o g ¹¹ ’

K m ( f , G ) =

II P_Gf — P o f II

II f — P o f II ’

где P O f – морфологическая проекция изображения f по пустой форме O с одной однородной областью.

Позднее были предложены усовершенствования и модификации данного подхода в работах [10], [11], однако основные идеи были основаны на проекции одного изображения на мозаичную форму другого изображения или класса изображений.

В работе [3] был предложен геометрический подход к сравнению изображений, основанный на морфологическом анализе Пытьева. Пусть f ( x,y ) из F – кусочно-постоянная двухмерная функция и изображение g ( x,y ) из G – аналогичная функция с m областями G = { G 1 ,…, G m }; g =( g 1 ,…, g m ) – вектор значений яркости; x Gj (x,y ) e {0,1} - характеристическая функция j -й области.

Введём дополнительно следующие обозначения: S - площадь кадра Q ; S i = II x _Fi ( x,y ) II — площадь области разбиения F i ; S j = II x Gj ( x,y ) II 2 - площадь области разбиения G j ; S .j =( x Ft ( x,y ), x Gj ( x,y )) — площадь пересечения F i n G j .

Среднеквадратичный эффективный коэффициент морфологической корреляции (СКМК) форм F и G определяется как km( f , g )=s;=i s m=i SS^^

=s m=i sl Kq (F. ’ G) KM( Gj, F.)’ где KQ (Fi, Gj) = S.j/S - нормированный коэффициент значимости пары областей Fi и Gj для оценки сходства разбиений F и G; KM2(Gj,Fi) = Sij / Sj – квадрат нормированного морфологического коэффициента парной корреляции пары областей Fi и Gj.

Методы нелинейного снижения размерности данных, тепловые ядра и диффузные фильтры

Традиционно основным методом (линейного) снижения размерности многомерных данных считался метод главных компонент (PCA). Суть его заключается в том, чтобы найти главные компоненты (собственные векторы матрицы ковариации данных) и перейти в линейное подпространство меньшей размерности, являющееся замыканием заданного числа наиболее значимых собственных векторов (значимость определяется величиной соответствующих собственных чисел).

Наиболее интересными и известными подходами в данном направлении являются: Isomap [12], Locally Linear Embedding (LLE) [13], Kernel Principle Compo- nent Analysis [14], Laplacian Eigenmaps [15], Hessian LLE [16], Manifold Sculpting [17] и ряд других.

Термины «тепловое ядро» и «тепловое рассеивание» были введены в [15]. В работах [5], [6], [18] была введена и развита теория диффузных операторов ( diffusion maps ). Тогда проблема снижения размерности с помощью диффузных операторов может быть решена следующим образом:

A p , q

= exp-

II v (p)-v (q )l Ге

у™-Iv(p)-v(q )Г

"Е ” е .

Линейная фильтрация изображения I с таким фильтром описывается выражением

I a ⁽ p ) = Е ^ap , q^{1 (} q ) .

q

Определение графа соседства G .

Формирование теплового ядра heat kernel H = || h ij || (матрица теплового обмена с параметром температуры t е R ). Если между точками i и j имеется связующее ребро, то

h ij = exp

I X - x j

2 g ²

У

в противном случае h ij =0.

Нормализация теплового ядра и получение ядра диффузии P = M ^–1 H, где M = || m ij || – диагональная матрица сумм H: m ii = Е i h ij .

Выбор масштабного параметра t .

Вычисление спектрального разложения матрицы P ^t с собственными числами

1 = Х ₀ >Х 1 >Х 2 >...

и соответствующими собственными функциями {ψ i }.

Отображение данных в пространство низкой размерности l путём выбора l максимальных собственных значений и перехода к новым координатам:

^X i =[^X 1 V i 1  ^2   ^ ^Х I V il f .

Ключевыми шагами здесь являются шаги 2 и 3, поскольку нормализация теплового ядра позволяет трактовать его как переходную матрицу Марковских случайных блужданий, а параметр t (степень матрицы P ^t ) позволяет рассматривать евклидово расстояние в новом пространстве как вероятность перехода из точки в точку за t шагов таких случайных блужданий.

Однако задачами снижения размерности применимость данного подхода к описанию формы не ограничивается. Например, в [6] можно найти описание целого ряда различных применений диффузных отображений в таких областях, как обработка изображений, комплексирование информации от различных датчиков, восстановление разреженных матриц и ряд других. В частности, в [6] описано приложение данной техники к анализу формы изображения (точнее, к задаче фильтрации изображения с сохранением его формы). В данной работе для каждой точки изображения I с координатами p = ( x p , y p ) вводится некоторый вектор признаков v ( p ), характеризующий её окрестность. В простейшем примере в качестве v ( p ) используется сама окрестность, например, 5x5. Далее выбирается е >0 и определяется Марковский фильтр

ТВ

ИК

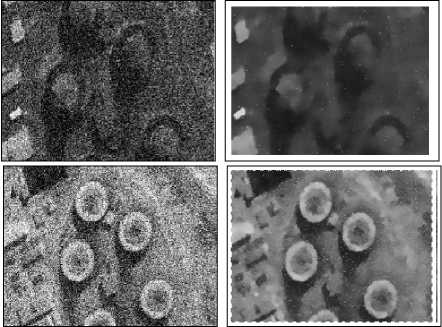
Рис. 1. Примеры диффузной фильтрации для удаления шума ТВ- и ИК-изображений

На рис. 1 представлены примеры диффузной фильтрации для удаления шума ТВ- и ИК-изображе-ний с ядром 5×5, как в и статье [6]. Форма изображений сохраняется при эффективной фильтрации изображений от шума.

В последние годы в отдельное и быстро развивающееся направление выделились дескрипторы формы, основанные на «тепловых ядрах» и диффузных преобразованиях, а также их спектральных и других производных характеристиках. Инвариантные описания форм как точечных множеств, представляющие собой диагональ теплового ядра (Heat Kernel Signature, HKS), были предложены в [20], [21], [22], [23]. В литературе также рассматриваются такие статистики, как распределение HKS (heat kernel signature distribution, HKSD) и «тепловой след (heat trace)». Существует и множество других модификаций этого подхода, часто называемого также «спектральным» подходом к описанию формы.

2. Диффузная морфология и сравнение изображений Обобщение морфологического анализа Пытьева с использованием тепловых ядер и диффузных фильтров

В основе спектральной теории диффузных отображений лежат симметричные нормированные диффузные операторы H, такие что ij ; ii ij; ij ji;

Vⁿ h = 1;V ⁿ h = 1.

Z—I i =1 j     ’ Z—1 j =1 J

В частном случае они задаются путём нормирования тепловых ядер вида kij = exp(-dj/е), где dij – расстояние между i-й и j-й точками многообразия в некотором исходном пространстве признаков.

Рассмотрим полутоновое изображение f(x,y) и определим дискретное расстояние по яркости между i-й и j-й точками изображения как f0,    если f(xi,y^ = f (xj,yj);

di = <

[да , в противном случае.

Тогда матрица сходства (тепловое ядро) будет иметь вид kj = exP(-dij /е) = Г

1 0,

если f ⁽ x i , y i ) = f ⁽ x j , y j );

в противном случае .

C точностью до формы записи это ничто иное, как матрица пиксельных отношений «пикселы равны по яркости» [4]:

to f ( x , y , u , v )

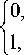
если f ( x , y ) * f ( u , v ); если f ( x , y ) = f ( u , v ).

При этом если изображение f относятся к пытьев-ской форме F , описываемой кусочно-постоянной моделью

n

f (x, y ) = E fi X Fi (x, У), i =1

тогда отношение tof имеет вид f1,    если V i: хF (x, y ) = x f (u, v);

to F ( x , y , u , v ) = ^                          -^V              -^V

[0,   в противном случае .

Проведём вероятностную нормировку:

uF = JJtof (x, y, u, v) du , aF (x, y, u, v) = tof (x, y, u, v)/(uF (x, y) uF (u, v)), что для кусочно-постоянного изображения формы F даёт aF (x, y, u, v) =

= J V S i , если 3 i : х F i ( x , У ) = X F i ( u , v ) = 1;

[0, в противном случае , где Si – площадь области разбиения Fi.

Таким образом, как мы видим, оказался сформирован линейный оператор (пытьевского проецирования), эквивалентно описывающий форму F , заданную набором отношений сходства to _F :

g F ( x , y , u , v ) = A f g ( x , y ) =

= JJ a F ( x , y , u , v ) g ( x , y ) d u d v .

Следует отметить, что || A F || ≤ 1, то есть это «диффузное» преобразование. При этом собственными функциями данного преобразования являются характеристические функции пытьевской формы { х и ( x,y )} (все с собственными числами 1), а собственным пространством является линейная комбинация собственных функций, то есть сама пытьевская форма (3) как линейное подпространство в пространстве изображений с ортогональным базисом из характеристических функций областей разбиения.

Таким образом, пытьевские проекторы являются частным случаем диффузных отображений, а пытьев-ские формы являются частным случаем собственных подпространств диффузных операторов. С учётом этого, обобщая пытьевскую терминологию, можно дать следующие определения.

Определение 1. Реляционной моделью диффузной формы F изображения f будем называть функцию парного отношения сходства точек изображения kF (x,y,u,v): QxQ^ [0,1], такую что:

k F ( x , y , u , v ) > 0;

k_F ( x , y , x , y ) > k_F ( x , y , u , v ) ;

k_F ( x , y , u , v ) = k_F ( u , v , x , y )

и при этом существует однозначная функция измерения сходства n, что n(f (x,y), f (u,v)) = kF (x,y,u,v).

Определение 2. Операторной моделью диффузной формы F будем называть оператор диффузного преобразования P F ,

PFg (x, y) = JJfi Pf (x, y,u, v) g (u, v) du dv, определяемый нормированным ядром pF(x,y,u,v), таким что:

P f ( x , y , u , v ) > 0;

P f ( x , y , x , y ) > P f ( x , y , u , v ) ;

JJ n P_F ( x , у , u , v ) d u d v = 1;

JJJJ n n p F ( x , У , u , v ) d x d y d u d v

< да .

При этом всякой реляционной модели диффузной формы может быть поставлена в соответствие её операторная модель:

P f ( x , У , u , v ) = k F ( x , y , u , v )/ JJ_n k F ( x , У , a , b )d a d b .

Определение 3. Диффузной формой F изображения f ( x, y ) назовём собственное пространство оператора диффузного преобразования P F

F = span{Х1ф1 (x,y),_,Xnфn (x,y)}, где {Xi,^,Xn} - собственные числа, а {ф1(x,y),^,фn(x,y)} - собственные функции оператора PF:

P f ф , - ( x , У ) = Х , ф , ( x , у ) , i = 1,^ n .

В частном случае выбор

n ( ^f ( ^x , У ) , ^f ( ^u , ^v ) )

1,

0,

если f ( x , y ) = f ( u , v );

в противном случае приводит к построению пытьевской морфологии, описывающей форму изображения на основе разбиения кадра на области равной яркости. Соответственно, диффузная форма становится в данном частном случае пытьевской формой вида (3), а для любого изображения g(x,y) e L2(Q) проекция на форму F может быть записана в явном виде (4).

В случае дискретного изображения f ( x, y ), заданного на множестве точек {( x i , y i )}, i = 1, ..., m , диффузный оператор представляет собой матрицу H (размера m x m ), такую что

^H ( x i , У. ) = Х mJ =1 h ij^{f (} x j , У ] ^X

Em j=1 j       .

коэффициента. В данном случае имеет место вычита-

Таким образом, мы построили обобщение проективной морфологии Пытьева, которое можно назвать диффузной морфологией двумерных изображений .

Метод взаимной привязки многоспектральных изображений на основе диффузной корреляции

Для взаимной привязки изображений различных спектральных диапазонов предлагается следующее обобщение морфологической корреляции с использованием диффузных операторов.

Как было указано выше, сравнение изображений f ( x, y ) и g ( x,y ) в рамках морфологии Пытьева осуществляется с помощью нормированных морфологических коэффициентов корреляции Пытьева (МКК). Данный коэффициент, естественно, удовлетворяет свойству K M ( f , F ) = 1, поскольку в проективной морфологии f = P F f. Однако диффузный морфологический оператор в общем случае не является проективным, так как представляет собой сглаживающий фильтр: || P F f || <  || f ||. Впрочем, естественно предположить, что степень сглаживания P F существенно меньше для изображений с похожими формами, чем для изображений с разными формами. Исходя из этого, предлагается определить морфологический коэффициент диффузной корреляции (МКДК) как отношение пытьевских коэффициентов:

ние среднего в скользящем окне, определяемом носителем теплового ядра диффузного фильтра. При этом сохраняются только локальные информативные особенности при анализе в соответствующих масштабах. Эти информативные элементы изображения g в случае, если форма G похожа на форму F , сохраняются или, в противном случае, размываются при фильтрации диффузным фильтром P F . Иными словами, оператор ( P F – P O ) в диффузной морфологии реализует известный приём морфологической нормализации изображения (рис. 2). Легко заметить, что при последовательном уменьшении эффективного размера теплового ядра свойства диффузной морфологической корреляции (7) будут стремиться к свойствам точеч-

ных и контурных корреляторов, которые используют для сравнения изображений лишь простейшие локальные особенности формы. Однако, как было сказано выше, диффузные операторы имеют естествен-

ный инструмент для анализа данных с использованием разных масштабных уровней – параметр t (число Марковских случайных блужданий). Описание формы изображения посредством набора диффузных операторов разного масштаба { P^t } позволяет производить морфологический анализ на различных мас-

а)

штабных уровнях.

K md ( g , F ) =

K m ( g , F ) = || P F g || || f || K M ( f , F ) || P F f |||| g || ^,

где K M ( f , F ) описывает степень собственного размытия f относительно F.

Следует отметить, что МКДК является корректным обобщением МКК, поскольку в случае проективной морфологии

II f l 1 = 1 \M k K md ( g , F ) = K m ( g , F ).

Кроме того, как и в МКК (5), для исключения неинформативной части яркости изображений перед непосредственно сравнением их необходимо нормализовать:

K md ( g , F ) =

|| P_Fg — P og\\ || f — P o f\\

|| P p f - P o f || || g - P o gW

где P O f – фильтрация изображения f по пустой диффузной форме O , в которой сходство всех пикселов в пределах носителя теплового ядра одинаковое.

При этом важно, что в диффузной морфологии такая нормализация не является тривиальным вычитанием среднего значения, как в случае пытьевского

в)

Рис. 2. Пример морфологической нормализации изображения: изображение f (а); изображение g (б);

г)

б)

изображение f, нормализованное по форме F(PF f – PO f) (в); изображение g, нормализованное по форме F (PF g – PO g) (г)

На практике, также как и для пытьевского коэффициента МКК, в задаче привязки фрагментов изображений предпочтительнее использовать квадрат МКДК, поскольку такая мера сходства имеет смысл статистического коэффициента детерминации между моделью (форма F ) и данными (изображение g ).

3. Вычислительная реализация и результаты экспериментов Быстрая реализация диффузных операторов

Расчёт результатов диффузной фильтрации с тепловым ядром формы

h ( p , q ) = exp

^^^^^^»

IIv (p)-v (q )l 12'£7

где v ( p ) – некоторый малый фрагмент изображения с центром p – вычислительно весьма затратная процедура даже в случае умеренных размеров v ( p ). В связи с этим при практической реализации описанного подхода предлагается заменить v ( p ) на упрощённый тип дескриптора точки – iLBP( p ) (intensity + LBP):

iLBP (p ) = ( m (p), LBP (p)), где m(p) – среднее значение яркости для v(p); LBP(p) – пороговый LBP [23] для v(p).

Соответственно заменяем исходную евклидову метрику сравнения двумерных фрагментов на специальную метрику сравнения iLBP-дескрипторов

II v ⁽ p ^)- v ⁽ q )l 1² ~

~ p| m ( p ) - m ( q )| |² + d ham ( LBP ( p ) , LBP ( q ) ) , где d ham – расстояние Хемминга, β – весовой коэффициент яркостной части iLBP. Кроме того, в предлагаемой реализации локальные бинарные паттерны хранятся как битовые массивы, а расчёт расстояния Хемминга производится посредством XOR-операции. Экспонента рассчитывается по табличным значениям. Среднее значение в скользящем окне рассчитывается быстрым алгоритмом с пересчётом скользящей суммы. В соответствии с этим использование iLBP позволяет ускорить время расчёта и получить форму тепловых ядер, очень похожую на исходную.

Текущая программная реализация обеспечивает время обработки около 300 мс при работе в одном потоке для изображения размера 640×480 для PC с конфигурацией Core i7 – 860 /8Gb/ GeForce GTX 680.

Использование технологии CUDA [24] позволяет дополнительно улучшить производительность алгоритма диффузной фильтрации. В текущей реализации алгоритм с использованием CUDA обрабатывает изображение размера 640×480 за 40 мс для той же конфигурации PC, то есть позволяет выполнять описанную процедуру сравнения изображений в реальном времени.

Результаты экспериментов по взаимной привязке ТВ- и ИК-изображений

Для изображений видимого (ТВ) и инфракрасного (ИК) диапазонов корреляционная функция вычислялась при сопоставлении заданного фрагмента ТВ с изображением ИК с использованием гистограммной сегментации методом динамического программирования (число мод гистограммы n =4). Значение корреляционной функции С ( x , y ) соответствовало результату её расчета при сравнении исходного сегментированного ТВ-фрагмента и текущего фрагмента ИК (форма-разбиение G ) без сегментации, отстоящего от начальной точки сопоставления на ( х , y ). Глобальный максимум корреляционной функции соответствует положению левого верхнего угла наиболее похожего на ТВ-фрагмент фрагмента ИК. Корреляционные функции оценивались для следующих мер сходства: взаимная информация (1), квадрат центрированного морфологического коэффициента

Пытьева (5), квадрат среднеквадратичного коэффициента морфологической корреляции (СКМК) (6), квадрат морфологического коэффициент диффузной корреляции (МКДК) (7).

Для оценки качества сравнения по форме использовались следующие показатели – отношение разности глобального максимума и среднего значения корреляционной функции к её СКО ( SNR ) и отношение значений центрированного глобального максимума и следующего по величине локального максимума в прямоугольной окрестности ξ глобального максимума ( E ):

SNR = |Ci-ц|/о; E = |Ci-ц|/|С2-ц|, где C1 = Cglob – значение глобального максимума корреляционной функции; C2 = Cloc(ξ) – первый локальный максимум вне прямоугольной окрестности ξ глобального максимума; μ – среднее значение корреляционной функции; σ – среднеквадратическое отклонение.

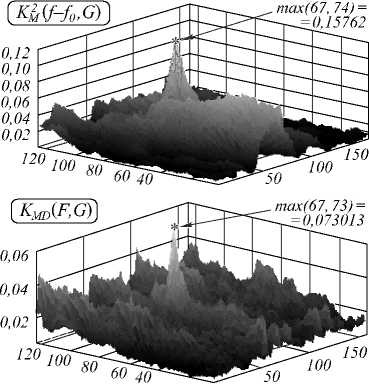
На рис. 3, 5 приведены четыре пары ТВ-и зашумленных аддитивным Гауссовским шумом ИК-изображений (примеры 1, 2 соответственно). Координаты точек совмещения ТВ- и ИК-фрагментов (левого верхнего угла фрагмента ТВ относительно левого верхнего угла ИК) – (38,48) и (67,73) для примеров 1, 2 соответственно, при этом допустимая погрешность при совмещении 1 пиксель по вертикали и горизонтали. Рис. 4, 6 содержат графики корреляционных функций ((а) взаимная информация (1), (б) МКК Пытьева (5), (в) СКМК (6), (г) МКДК (7)). Численные данные приведены в табл. 1, 2.

Табл. 1. Численные данные сравнения ТВ- и ИК-фрагментов (Пример 1)

Мера сходства	Макс.	SNR	E
MI ( F , G )	0,11779	5,2488	1,8078
K M 2 ( f–f 0 , G )	0,11652	4,4419	1,5112
K M 2 ( F , G )	0,45184	4,6458	1,8060
KMD ( f , G )	0,11051	9,7336	5,4148

Табл. 2. Численные данные сравнения ТВ- и ИК-фрагментов (Пример 2)

Мера сходства	Макс.	SNR	E
MI ( F , G )	0,12510	6,2888	1,6984
K M 2 ( f-f 0 ,G );	0,15762	6,0133	1,6097
K M 2 ( F , G )	0,41022	6,6922	1,6646
KMD ( f , G )	0,07371	9,0106	1,8946

В соответствии с этими экспериментами можно сделать следующие выводы. Предложенный коэффициент МКДК обеспечивает более высокий и острый пик корреляционной функции по сравнению с другими мерами сходства. Например, по сравнению с критерием взаимной информации в некоторых экспериментах МКДК даёт в 1,5-2 раза лучшее значение SNR. Пример 2 показывает также более высокую устойчивость МКДК к шуму по сравнению как с взаимной информацией (1), так и с морфологическими коэффициентами МКК (4) и СКМК (5).

а)

б)

Рис. 3. Пример 1: эталонный ТВ-фрагмент (а); тестовое ИК-изображение (б);

сегментированный ТВ-фрагмент (в)

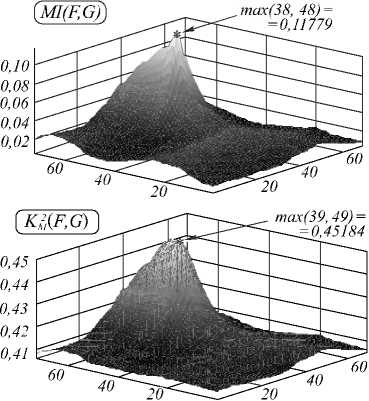
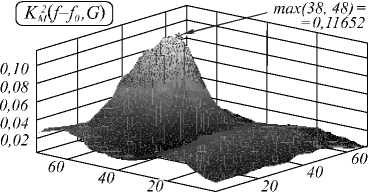
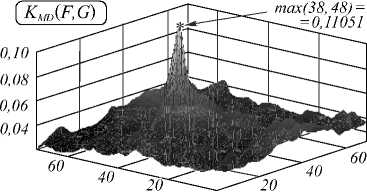
Рис. 4. Графики корреляционных функций (Пример 1)

б)

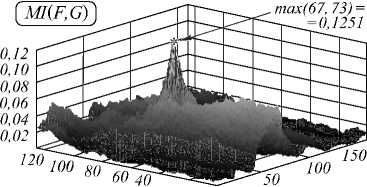
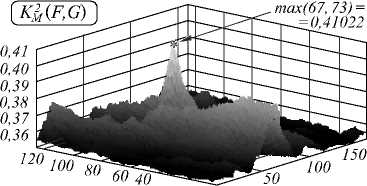
Рис. 6. Графики корреляционных функций (Пример 2)

Рис. 5. Пример 2: эталонный ТВ-фрагмент (а); тестовое ИК-изображение (б); сегментированный ТВ-фрагмент (в)

Заключение

В статье описан новый математический аппарат для сравнения изображений по форме на основе тепловых ядер и диффузных операторов, который пред- ложено называть диффузной морфологией. Диффуз ная морфология представляет собой непосредствен ное обобщение морфологического анализа изображе ний Пытьева. Все средства анализа форм, ранее пред ложенные в рамках морфологии Пытьева, могут быть также получены и в диффузной морфологии путём использования согласованного с формой изображения диффузного оператора вместо морфологического проектора на эту форму.

Для непосредственного применения в практических приложениях в статье предложен новый инструмент сравнения изображений по форме – морфологический коэффициент диффузной корреляции (МКДК), реализуемый на основе быстрой диффузной фильтрации с использованием нового типа точечного дескриптора признаков iLBP. Такая вычислительная реализация позволяет производить взаимную привязку изображений на основе МКДК в реальном времени.

Проведено сравнительное экспериментальное исследование предложенной диффузной корреляции, взаимной информации, коэффициента морфологической корреляции Пытьева и среднеквадратичного коэффициента морфологической корреляции (СКМК) в задаче взаимной привязки фрагментов ТВ- и ИК-изображений. Качество получаемых двумерных корреляционных функций оценивалось посредством двух статистик: отношение сигнал-шум (SNR) и превышение первого пика (максимума) над вторым. В проведённых экспериментах с реальными данными аэрофотосъёмки МКДК показал существенно лучшую форму корреляционного поля. Это позволяет утверждать, что предложенная в данной работе морфологическая диффузная корреляция – лучшая из известных на сегодня оценок сходства по форме для подобного класса задач сравнения изображений.

Работа выполнена при поддержке грантов РФФИ № 13-08-01071, 14-07-00914 и при поддержке гранта Президента РФ (ВНШ-3477.2014.8).