Сравнение эффективности каналов насадок регенераторов по результатам расчета в пакете ANSYS CFX

В качестве определяющих температур для теплообменной стенки и воздуха на входе были приняты усредненные по высоте насадки температуры реального доменного воздухонагревателя [1]. Давление воздуха на выходе было принято равным 0,2 МПа; площадь входного сечения была принята одинаковой для всех каналов и равной S = 0,045 2 = 2,025 - 10 - 3 м²; длина каждого канала составляла L = 1,5 м.

Для получения установившегося профиля течения начальный участок гидродинамической стабилизации был выбран равным 1 м. В качестве определяющих уравнений для расчета использовались уравнения сплошности, количества движения и тепловой энергии. Ориентация канала в пространстве была учтена включением вектора массовых сил в уравнение количества движения, в качестве модели турбулентности была использована k– ω SST-модель.

Круглый канал . Сетка представляет собой совокупность тетраэдрических и призматических элементов; максимальная длина ребра элемента не превышает 3 мм, толщина пограничного слоя для среднего значения числа Рейнольдса определяется как

8 = 0,035 L Re ^-1/7 = 0,035 - 0,05 - 10000 ^{- 1/7} = 0,47мм. (1)

Методом последовательных приближений были определены параметры призматического слоя: q = 1,1, h 1 = 0,02 мм, n = 15. При этом толщина слоя:

n                    15

H 15 = h 1       = 2-Ю , , , = 0,63мм, (2)

n - 1             1,1 - 1

где H – высота призматического слоя, h 1 – высота первой призмы, q – знаменатель прогрессии, n – число рядов призматических элементов. Высота десяти первых призматических слоев:

n                    10

H ₁₀ = h 1 q ----= 2 - 10 ^{- 5 1}----- = 0,319 мм. (3)

n - 1             1,1 - 1

Таким образом, толщина пограничного слоя находится в интервале между 10-м и 15-м призматическими слоями, что обеспечивает необходимую точность при использовании пристеночной функции [2]. Характеристики расчетной сетки: количество узлов 550 013, количество элементов 1 700 772, в том числе тетраэдрических 953 188, призматических 747 584. На входе в расчетный канал задавался плоский профиль скорости, причем скорость рассчитывалась по фиксированному числу Рейнольдса 104 и температурным зависимостям для теплофизических характеристик потока среды при температуре на входе tв = 560 ºС, температура стенки tс = 820 ºС.

Задание начальных условий в стационарном режиме обычно не применяется, но помогает сократить время компьютерного расчета. В данном случае это целесообразно, так как модель состоит из большого количества конечных элементов. Начальные условия распространяются равномерно в пределах всей расчетной области: начальная температура t = 560 ºС; начальное абсолютное давление p = 0,2 МПа, начальная скорость в направлении оси канала w = 8,93 м/с, в качестве масштаба времени было принято 20% времени пребывания.

Расчеты показали, что коэффициент гидравлического сопротивления убывает с увеличением числа Рейнольдса от 6300 до 16000 по зависимости

X = 131,07/Re ⁰ , ⁸⁴²⁵ ,             (4)

число Нуссельта увеличивается в этом же интервале чисел Рейнольдса по зависимости

Nu ср = 0,°°87Re °,8 ³⁵ .            (5)

Квадратный канал. Тип сетки аналогичен типу сетки круглого канала. Толщина пограничного слоя

8 = 0,035 L Ke L ^ = °,°35 - 0,045 - lOOOO" ¹/⁷ = 0,42мм. (6)

Методом последовательных приближений были определены параметры призматического слоя: q = 1,1; h1 = 0,02 мм; n = 15. При этом толщина слоя n                    15

H 15 = h 1 q ----= 2 • 10 ^{- 5} -,------ = 0,63 мм. (7)

n - 1            1,1 - 1

Высота десяти первых призматических слоев: n                    10

H ₁₀ = h 1 q ----= 2Л0 ^{- 5}------ = 0,319мм. (8)

n - 1             1,1 - 1

Толщина пограничного слоя также находится в интервале между 10-м и 15-м призматическими слоями. Характеристики полученной сетки: количество узлов 604 395, количество элементов 1 795 862, в том числе тетраэдрических 941 222, призматиче- ских 854 640. Граничные и начальные условия были заданы такими же, как для круглого канала.

Результаты определения коэффициента гидравлического сопротивления можно представить в виде формулы

X = 50,734/Re ⁰ , ⁷⁴⁶⁵ , (9) зависимость числа Нуссельта от числа Рейнольдса имеет вид

Nu = 0,00727 Re ⁰ , ^8525. . (10)

Диффузорно-конфузорный канал. Исследованный участок канала представлял собой сочетание конических элементов высотой 30 мм, соединенных чередующимися широкими и узкими основаниями диаметром 50 и 42 мм соответственно.

Тип конечно-элементной сетки аналогичен круглому каналу. Шаг сетки – не более 5 мм. Для повышения точности расчета в дополнение к призматическим слоям в области переменного сечения модели задано местное сгущение сетки с максимальным шагом 2 мм и коэффициентом роста 1,2. Определяющий линейный размер совпадает с диаметром круглого канала, поэтому в повторном определении примерной толщины пограничного слоя нет необходимости. Характеристики сетки: количество узлов 355 626, количество элементов 1 141 047, в том числе тетраэдрических 680 247, призматических 460 800 .

На рис. 1 показано распределение турбулентной кинетической энергии в области переменного сечения, а также притупление профиля скорости на выходе из него, что также является следствием турбулизации потока. Из рисунка очевидно, что турбулизация происходит в местах отрыва пограничного слоя при расширении канала. При этом турбулентная кинетическая энергия возрастает лавинообразно по ходу движения среды.

В результате моделирования получены зависимости для коэффициентов сопротивления

X = 7,64/Re ⁰ , ⁴⁵ (11)

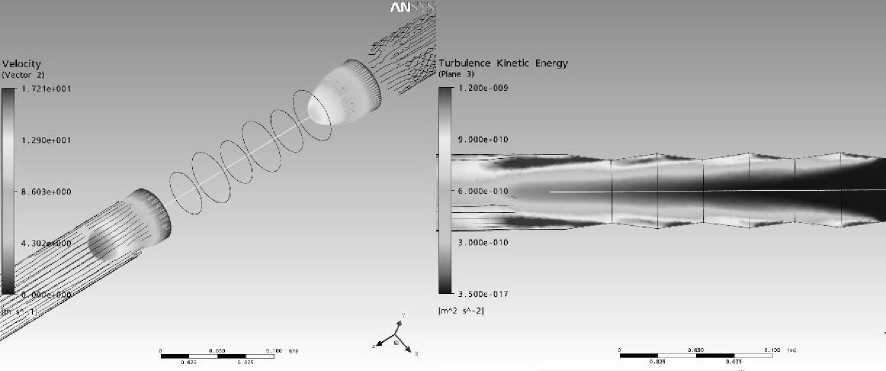
Рис. 1. Профили скорости и распределение энергии

и числа Нуссельта

Nu ср = 0,0131Re ⁰ , ⁸¹ .           (12)

Канал со сферическими лунками имеет квадратное сечение с нанесенными на внутренней поверхности сферическими углублениями. Авторы статьи [3] показали, что оптимальной относительной глубиной лунки с точки зрения теплообмена являются значения, близкие к интервалу от 0,05 до 0,3. Под относительной глубиной понимается отношение d/h , где d – диаметр образующей лунку сферической поверхности, h – максимальная глубина лунки. При подборе глубины лунки с точки зрения вихреобразования при помощи моделирования линий тока в ее окрестности в ANSYS CFX было замечено, что при значениях, превышающих указанный выше интервал, в лунке образовывались застойные зоны и вихрь не покидал лунки. При слишком малых значениях глубины практически не происходило вихреобразования. Поэтому было выбрано значение d/h = 0,15 с радиусом скругления острой кромки r = 4 мм. Диаметр образующей лунку сферы выбран равным 40 мм из конструктивных соображений.

Тип конечно-элементной сетки – тетраэдрическая с призматическими слоями у стенки. Шаг сетки – не более 5 мм. Призматический слой аналогичен призматическому слою квадратного канала. Для повышения точности расчета в луночной области модели задано местное сгущение сетки с максимальным шагом 1 мм и коэффициентом роста 1,2. Определяющий линейный размер совпадает с диаметром квадратного канала, поэтому в повторном определении примерной толщины пограничного слоя нет необходимости. Характеристики сетки: количество узлов 1359 291, количество элементов 5 275 646, в том числе тетраэдрических 3 959 996, призматических 1 315 650.

Граничные, начальные условия и температурное состояние стенки были выбраны такими же, как и в расчетах гидродинамики в каналах круглого, квадратного и диффузорно-конфузорного сечений. Результаты моделирования можно описать следующими зависимостями:

X = 0,9897/Re ⁰ , ²⁵²⁵ ,           (13)

Nu ср = 0,041Re ^0,8825 .           (14)

Сопоставляя данные расчетов (4)–(5) и (9)– (14), можно выстроить гомологический ряд, который характеризует динамику изменения показателей сопротивления X и теплоотдачи Nuср при интенсификации процесса в последовательности: «круглый»,     «квадратный»,     «диффузорно конфузорный» и «луночный» каналы. Ряд для λ: 1; 0,886; 0,534; 0,300 и для Nuср: 1; 1,021; 0,970; 1,057.

Как показали результаты моделирования, сопротивление участка с лунками при некоторых значениях числа Re превышает значения для других каналов. При этом коэффициент теплоотдачи имеет относительно низкие значения. Это объясняется тем, что в лунках имеет место отрыв пограничного слоя и образуется область пониженного давления, что снижает полную теплоемкость воздуха. В то же время в аэродинамическом следе поверхности с лунками было обнаружено заметное возрастание коэффициента теплоотдачи и снижение гидравлического сопротивления. Поэтому дополнительно был рассчитан контрольный участок сразу за луночной поверхностью. Явление интенсификации теплообмена и снижения сопротивления в аэродинамическом следе луночной поверхности представляет определенный интерес для дальнейших исследований.

Процессы, происходящие в этой области, можно проследить на рис. 2 и 3.

При рассмотрении интегральных зависимостей на рис. 4 и 5 следует сделать вывод о том,

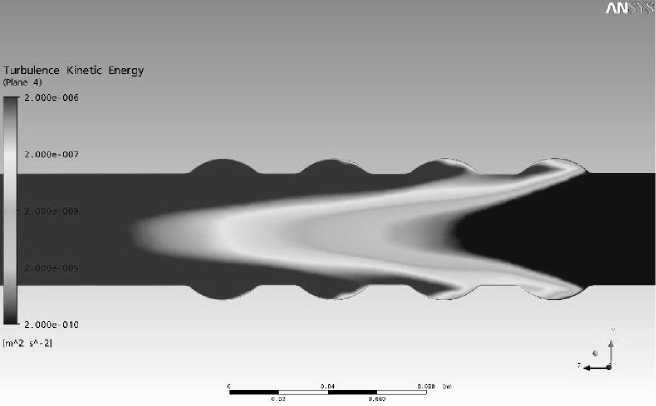
Рис. 2. Распределение турбулентной кинетической энергии

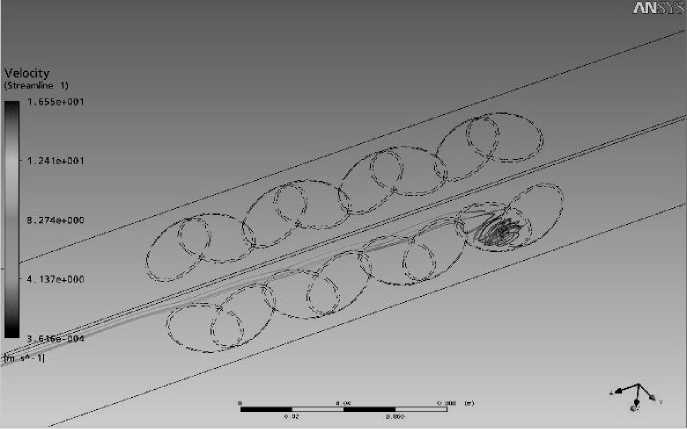
Рис. 3. Образование вихря в лунке первого ряда

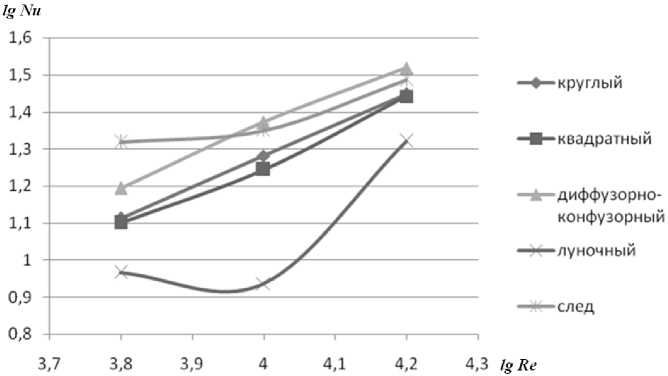
Рис. 4. Зависимость логарифма числа Нуссельта от логарифма числа Рейнольдса

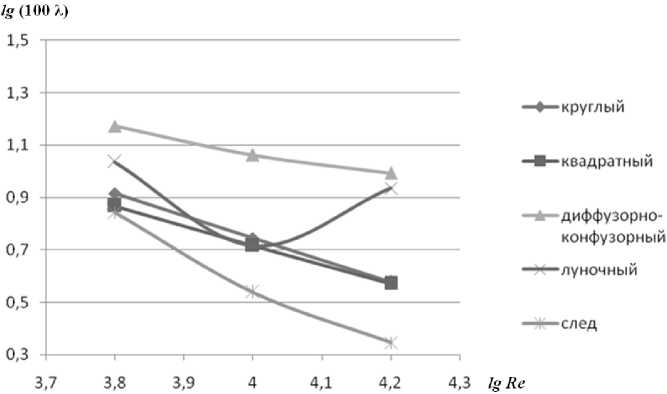
Рис. 5. Зависимость гидравлического сопротивления (lg100λ) от логарифма числа Рейнольдса что при явно нелинейной зависимости для канала с луночной поверхностью необходимо принимать другие методы аппроксимации для получения средних по поверхности значений.

Вывод

Полученные с помощью пакета ANSYS CFX теплогидравлические характеристики ряда насадок регенераторов позволяют произвести сравнительные расчеты по оптимизации размеров каналов при последующей адаптации данных к фактическим условиям работы насадок.