Сравнение эффективности различных подходов к формированию популяции при решении задач многокритериальной нестационарной оптимизации
Автор: Рурич М.А., Вахнин А.В., Сопов Е.А.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 2 т.23, 2022 года.
Бесплатный доступ
Многокритериальная нестационарная оптимизация является недостаточно изученным на данный момент классом задач оптимизации, однако представляет собой большую практическую ценность. В задачах многокритериальной нестационарной оптимизации целевые функции, их параметры и ограничения, накладываемые на область поиска, изменяются во времени, из этого следует изменение решения задачи. При возникновении изменений в задаче алгоритму необходимо адаптироваться к изменениям таким образом, чтобы скорость сходимости к решению задачи была достаточно высокой. Работа посвящена сравнению эффективности использования трех разных подходов к формированию популяции при возникновении изменений в задаче многокритериальной нестационарной оптимизации: использование полученных на предыдущем шаге решений, случайная инициализация популяции и частичное использование предыдущих решений. В первой части статьи приводится классификация изменений, возникающих в задачах этого типа; рассматриваются существующие на данный момент подходы к решению задач, основанные на использовании эволюционных алгоритмов. В ходе исследования при решении задач многокритериальной нестационарной оптимизации используются алгоритмы многокритериальной оптимизации NSGA-2 и SPEA2, для сравнения подходов к формированию популяции используется набор тестовых задач. Полученные результаты были обработаны с помощью статистического критерия Манна - Уитни. Было выявлено, что скорость изменений в задаче влияет на эффективность использования при формировании популяции решений, полученных в предыдущий момент времени.
Многокритериальная оптимизация в нестационарной среде, оптимизация в нестационарной среде, многокритериальная оптимизация, эволюционные алгоритмы
Короткий адрес: https://sciup.org/148324805
IDR: 148324805 | УДК: 519.85 | DOI: 10.31772/2712-8970-2022-23-2-227-240
Текст научной статьи Сравнение эффективности различных подходов к формированию популяции при решении задач многокритериальной нестационарной оптимизации
Многокритериальная оптимизация в нестационарной среде (dynamic multi-objective optimization, DMOO) является сложным и на данный момент недостаточно изученным классом задач оптимизации. В подобных задачах целевые функции, их параметры и ограничения, накладываемые на область поиска, могут изменяться во времени [1]. При этом целевые функции в данном случае представляют собой «черный ящик», следовательно, вид целевых функций и их свойства остаются неизвестными, а также отсутствует возможность вычисления производных, что значительно затрудняет выбор подходящего метода для решения этого класса задач. На данный момент предложено некоторое количество подходов к решению задач, однако эти подходы могут обеспечить успешное решение задачи только в случае, если она имеет строго определенный вид – из этого следует, что необходимо продолжать исследование подходов для решения такого типа задач.
Многокритериальная нестационарная оптимизация
Задача DMOO может быть представлена как совокупность двух других задач оптимизации: задачи многокритериальной оптимизации (multi-objective optimization, MOO) и задачи оптимизации в нестационарной среде (dynamic optimization, DO).
Особенностью задачи многокритериальной оптимизации является наличие двух или более целевых функций, которые должны быть оптимизированы одновременно. Таким образом, при нахождении решения задачи необходимо учитывать значения всех целевых функций. Формально задача многокритериальной оптимизации может быть представлена как
{ f 1( x ), f 2( x ),..., fk ( x )} → m i n , (1)
x где f - набор оптимизируемых функций; i е [1, k]; к - количество целевых функций; x - вектор решения из допустимой области S.
Как было сказано выше, целевые функции в большинстве практических задач конфликтуют между собой, т. е. редко существует такое решение, которое было бы оптимальным сразу по всем целевым функциям. Зачастую приходится выбирать компромиссное решение, при котором значения целевых функций являются приемлемыми в некотором смысле, используя множество, оптимальное по Парето (МП) [2].
Множество прикладных задач оптимизации находятся в условиях, изменяющихся с течением времени. Такие задачи называются задачами оптимизации в нестационарной среде или задачами оптимизации, зависящими от времени (time-dependent optimization problems). Особенность задач DO заключается в том, что поисковое пространство задачи и ландшафт целевой функции изменяются с течением времени, а вместе с тем изменяется и оптимальное решение задачи [3].
Во многих публикациях, рассматривающих DO, для поиска решения такого типа задач предлагается использовать эволюционные алгоритмы (ЭА). Класс ЭА является хорошим инструментом для решения DO, поскольку эти алгоритмы вдохновлены естественными системами, которые постоянно находятся под воздействием изменяющихся факторов. ЭА оперируют популяцией решений, поэтому в том случае, когда оптимальное решение задачи изменяется, одно из имеющихся решений может быть достаточно близким к оптимальному.
Задача DO может быть формально определена следующим образом [3]:
f ( x , a ( t )) ^ min, (2)
x где f - целевая функция; x - вектор решения из поискового пространства; а(t) - вектор некоторых параметров целевой функции, изменяющихся во времени; t е [0, 7] - интервал времени, в котором происходит рассмотрение задачи.
В практических задачах вектор а ( t ) может представлять собой параметры внешней среды (такие как, например, температура, доступные ресурсы и т. д.), которые оказывают влияние на целевую функцию. В искусственно сгенерированных тестовых задачах, например, в задачах с перемещаемыми областями экстремума - впадинами, это может быть параметр их глубины, ширины и расположения. Вектор а ( t ) также может включать в себя и другие изменяемые параметры, например, количество переменных целевой функции [4].
Большинство существующих работ по DO рассматривают эту задачу как последовательность задач на дискретном интервале времени t е {0,..., 7 }:
{ f ( x , а (1)) ^ min, f ( x , а (2)) ^ min,..., f ( x , а(T )) ^ min} . xx x
Определение задачи DMOO может быть представлено следующим образом [4]:
{ f 1 ( x , а ( t )), f , ( x , а ( t )),..., fk ( x , а ( t ))} ^ min . x
Сложность многокритериальной оптимизации в нестационарной среде заключается в том, что вместе с изменением задачи происходит изменение фронта Парето (ФП).
В публикациях, посвященных DMOO, приводятся различные способы классификации таких задач, в зависимости от вида изменений [4]:
-
- классификация на основе скорости изменений. С увеличением скорости изменений уменьшается допустимое время для адаптации алгоритма к возникающим изменениям, что усложняет задачу;
-
- классификация на основе степени изменений. Изменения могут быть значительными и незначительными. В случае незначительных изменений имеется возможность использования информации, полученной из предыдущего состояния;
-
- классификация на основе предсказуемости изменений. Изменения могут быть регулярными (циклическими) и, как следствие, предсказуемыми, либо случайными (ациклическими);
– Классификация на основе изменяемости ФП и МП. Этот вариант классификации включает в себя 4 типа задач: оптимальное МП изменяется, оптимальный ФП не изменяется; и оптимальное МП, и оптимальный ФП изменяются; оптимальное МП не изменяется, оптимальный ФП не изменяется; и оптимальное МП, и оптимальный ФП не изменяются. В последнем случае могут изменяться, например, только локальные экстремумы.
Можно выделить два способа учитывания происходящие в задаче изменения [5]:
-
1 . Рассматривать каждое изменение как возникновение новой задачи оптимизации, которую необходимо решить с нуля.
-
2 . Использовать информацию о предыдущем шаге поиска решения, чтобы ускорить процесс оптимизации после изменения.
При этом первый подход не всегда является подходящим из-за ограничений по времени. Во втором случае алгоритм должен быть способен адаптироваться к изменениям, т. е. должно присутствовать достаточное разнообразие в используемых решениях, чтобы алгоритм мог гибко реагировать на изменения.
В работах, посвященных DMOO, рассматриваются подходы к решению таких задач, основанные на существующих ЭА:
-
- подходы, основанные на введении механизмов в ЭА, способствующих увеличению разнообразия (diversity based [6,7]);
-
- подходы, основанные на предсказании изменений в задаче (prediction based [8; 9]);
-
- подходы, основанные на использовании информации о предыдущем состоянии в задаче при поиске решения в текущем состоянии (memory based [10; 11]);
-
- подходы, основанные на использовании нескольких популяций, эволюционирующих параллельно друг другу и обменивающихся информацией (multi-population based [12; 13]).
Применение. ЭА для решения задач DMOO на данный момент недостаточно изучено, тогда как применение ЭА для решения задач MO развито значительно больше – для этого класса задач существует ряд широко применяемых методов, основанных на ЭА, таких как, например, NSGA-2 и SPEA2, которые позволяют аппроксимировать ФП с высокой точностью. Поэтому имеет смысл использования уже существующих методов MO при формировании подходов к решению задач DMOO.
Алгоритм NSGA-2
NSGA-2 ( Non-dominated Sorting Genetic Algorithm – генетический алгоритм сортировки недоминируемых решений ) является одним из самых известных алгоритмов для решения задачи многокритериальной оптимизации. На рис. 1 схематично представлен принцип работы двух механизмов сортировки решений, использующихся в NSGA-2: сортировка недоминируемых решений (Non-dominated sorting) и сортировка по степени скученности (Crowding distance sorting) [14].
Сортировка недоминируемых решений заключается в следующем. Общая популяция R t состоит из популяции родителей Pt и популяции их потомков Qt , ее размер составляет 2 N , где N – размер популяции. Далее решения в множестве R t сортируются следующим образом: в подмножество F 1 включаются все недоминируемые решения (т. е. решения, для которых нет доминирующих решений в популяции) – это называется первым недоминируемым фронтом; в подмножество F 2 включаются решения, которые являются недоминируемыми в рамках множества { R t / F 1 } (множество R t , исключая подмножество F 1 ) – это называется вторым недоминируемым фронтом и т. д.
Далее происходит формирование новой популяции Pt+1: подмножества недоминируемых фронтов поочередно, начиная с первого, добавляются к популяции Pt+1 до тех пор, пока размер подмножества очередного недоминируемого фронта не будет превышать доступный размер Pt+1. В этом случае производится сортировка решений по степени их скученности: для решения i вычисляется расстояние до соседних решений (рис. 2). Таким образом в популяцию попадают разнообразные решения.
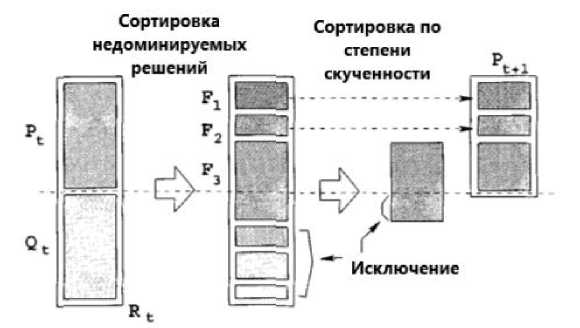
Рис. 1. Механизмы сортировки в NSGA-2 [14]
Fig.1. Procedure of sorting a population in NSGA-2 [14]
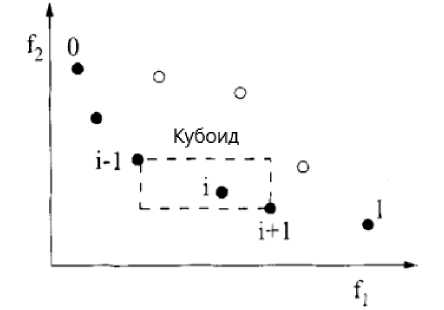
Рис. 2. Сортировка по степени скученности в NSGA-2 [14]
Fig. 2. Crowding distance sorting in NSGA-2 [14]
После чего к новой популяции Pt+1 применяются операторы селекции, рекомбинации и мутации.
Алгоритм SPEA2
Алгоритм SPEA2 (Strength Pareto Evolutionary Algorithm) является так же одним из самых популярных алгоритмов многокритериальной оптимизации. Одной из его особенностей является то, что наряду с популяцией решений в алгоритме используется архив недоминируемых решений (external set – внешнее множество) [15]. Для поддержания заданного количества индивидов, хранящихся в архиве, выполняется их кластеризация по степени удаленности друг от друга, в результате чего в архиве остается только представитель кластера. Использование архива решений позволяет алгоритму лучше в сравнении с другими алгоритмами аппроксимировать фронт Парето.
Другой особенностью алгоритма является подсчет пригодности индивидов. Для начала каждому индивиду i в популяции P t и во внешнем множестве P t* присваивается значение «силы» S , представляющее собой количество индивидов, которые доминируют над рассматриваемым индивидом [15]:
S (j) = {j I j G Pt+ P A l>j}|, (5) где означает доминирование по Парето. Однако высокое значение «силы» не гарантирует, что решение находится достаточно близко к фронту Парето. Поэтому далее вычисляется значение R для каждого индивида, которое является суммой значений «сил» индивидов, домини- рующих над рассматриваемым,
R ( i) = L S ( j ).
j G P t + P*, jyi
Таким образом, значение R = 0 соответствует недоминируемому решению (рис. 3):
с-——* недоминируемое решение 2
*--—• доминируемое решение
О о о 5 о
9 о
12О о оо
Рис. 3. Ранжирование решений в SPEA2 [15]
Fig. 3. Ranking of solutions in SPEA2 [15]
Результирующая пригодность F ( i ) индивида вычисляется как величина, обратная к значению R :
F ( i ) =----1---. (7)
1 + R ( i ) (7)
После этого к популяции решений применяются операторы турнирной селекции, рекомбинации и мутации.
Описание численных экспериментов
При использовании алгоритма многокритериальной оптимизации задача нестационарной оптимизации в каждый момент времени t рассматривается как отдельная задача оптимизации. Возможны два варианта формирования начальной популяции при переходе от одного момента времени к следующему:
-
1. Инициализировать популяцию случайным образом, т. е. производить рестарт алгоритма.
-
2. Использовать популяцию решений, полученных в предыдущий момент времени.
-
3. Использовать популяцию решений, одна часть которых была получена в предыдущий момент времени, а другая – инициализирована случайным образом.
Необходимо проверить, имеется ли отличие в точности полученных решений и скорости сходимости между этими тремя способами. Далее эти способы будут рассмотрены на примере использования алгоритмов многокритериальной оптимизации NSGA-2 и SPEA2.
В качестве тестовых задач многокритериальной нестационарной оптимизации был взят набор задач CEC2018 Dynamic Multi-objective Optimization Benchmark Problems, который включает в себя задачи различного вида. В табл. 1 представлены характеристики задач, приведенных в [16].
Таблица 1
|
Задача |
К-во ЦФ |
Вид изменений |
Примечания |
|
DF1 |
2 |
Смешанная выпуклость-вогнутость, изменение положения оптимумов |
Нестационарные ФП и МП |
|
DF2 |
2 |
Изменение положений оптимумов |
Стационарный выпуклый ФП, нестационарное МП |
|
DF3 |
2 |
Смешанная выпуклость-вогнутость, изменение зависимости между переменными, изменение положения опти-мумов |
Нестационарные ФП и МП |
|
DF4 |
2 |
Изменение зависимости между переменными, изменение значений границ МП и ФП |
Нестационарные ФП и МП |
|
DF5 |
2 |
Изменение числа вогнутых и выгнутых областей, изменение положения опти-мумов |
Нестационарные ФП и МП |
|
DF6 |
2 |
Смешанная выпуклость-вогнутость, мультимодальность, изменение положения оптимумов |
Нестационарные ФП и МП |
|
DF7 |
2 |
Изменение диапазона ФП и положения оптимумов |
Нестационарные ФП и МП, стационарный центроид МП, выпуклый ФП |
|
DF8 |
2 |
Смешанная выпуклость-вогнутость, изменение положения оптимумов, точки МП имеют регулярную структуру распределения |
Нестационарные ФП и МП, стационарные центроиды МП, зависимость между переменными |
|
DF9 |
2 |
Изменение числа несоединенных сегментов ФП и положения оптимумов |
Нестационарные ФП и МП, зависимость между переменными |
|
DF10 |
3 |
Смешанная выпуклость-вогнутость, изменение положения оптимумов |
Нестационарные ФП и МП, зависимость между переменными |
|
DF11 |
3 |
Изменение размера области ФП, диапазона ФП и положения оптимумов |
Нестационарные ФП и МП, вогнутый ФП, зависимость между переменными |
|
DF13 |
3 |
Изменение числа несоединенных сегментов ФП, изменение положения оп-тимумов |
Нестационарные ФП и МП, ФП может быть непрерывным вогнутым или выгнутым сегментом, либо несколькими несвязными сегментами |
|
DF14 |
3 |
Изменение числа вогнутых и выгнутых областей, изменение положения опти-мумов |
Нестационарные ФП и МП, зависимость между переменными |
Характеристики тестовых задач
Вид задач изменяется в зависимости от значения параметра t . Момент времени t в тестовых задачах из данного набора определяется следующим образом:
1 т t =
-
nt LT t
где n t – интенсивность изменений; τ = i∙n ; i – номер итерации задачи; n – количество итераций алгоритма оптимизации; τ t – скорость изменений.
Для оценки точности полученных решений для задач многокритериальной оптимизации используется мера IGD (Inverted Generational Distance), которая показывает степень различия между исходным ФП P и найденным ФП P * [17]. Для задач нестационарной многокритериальной оптимизации используется усредненная мера MIGD:
TTn Pt i
MIGD = 1 E IGD ( P t '■ P t ) = 7 EE ~ •
T t=1 T t=1 i=1 nPt где nPt = |Pt|; dti – эвклидово расстояние между i-м элементом Pt и ближайшим к нему элементом Pt*; T – количество итераций задачи.
Также используется мера Hypervolume , которая показывает степень удаленности фронта от некоторой наихудшей точки (reference point), которая задается вручную [18]. Для задач нестационарной многокритериальной оптимизации также используется усредненная мера MHV:
T
(
MHV = 7 X HV t ( P ), T t = 1
где HVt – оператор гиперобъема. В [16] предлагается задавать наихудшую точку как ( z 1 + 0,5, z 2 + 0,5, …, zm + 0,5), где z j – максимальное значение j -й целевой функции в исходном ФП в момент времени t ; m – число целевых функций.
При проведении численных экспериментов использовались следующие значения параметров тестовых задач:
-
- интенсивность изменений n т равна 10;
-
- количество итераций задачи T равно 30;
-
- количество переменных задачи равно 10.
Численные эксперименты проводились с использованием двух разных значений скорости изменений τ t : 10 (быстрые изменения) и 30 (медленные изменения) для того, чтобы проверить, дает ли лучший результат отсутствие рестарта при более медленных изменениях в задаче.
Также для алгоритмов NSGA-2 и SPEA2 размер популяции был задан равным 50 и число поколений равным 30. Каждая тестовая задача была решена 20 раз, результаты усреднялись.
Полученные результаты
В табл. 2 представлены средние значения метрики IGD для каждой тестовой задачи при медленной и быстрой скорости изменений и при использовании алгоритмов NSGA-2 и SPEA2. Между собой сравниваются результаты, полученные при использовании рестарта в алгоритме (инициализация популяции случайно), без использования рестарта (использование популяции, полученной в предыдущий момент времени) и с рестартом 50 % (одна половина популяции инициализируется случайно, а вторая половина является случайно отобранными решениями из популяции, полученной в предыдущий момент времени). В табл. 3 представлены средние значения метрики HV.
Обработка результатов производилась с помощью статистического критерия Манна – Уитни. Зеленым цветом выделены статистически наилучшие значения метрик (в рамках использованного алгоритма); выделение нескольких столбцов цветом означает, что различия между ними статистически незначимы.
Таблица 2
Значения метрики IGD в зависимости от различной инициализации популяции при медленных и быстрых изменениях для алгоритмов NSGA-2 и SPEA2
|
Медленные изменения |
||||||
|
Задача |
NSGA-2 |
SPEA2 |
||||
|
С рестартом |
Без рестарта |
Рестарт 50 % |
С рестартом |
Без рестарта |
Рестарт 50 % |
|
|
DF1 |
0,16626 |
0,05562 |
0,06047 |
0,35837 |
0,19831 |
0,14915 |
|
DF2 |
0,4249 |
0,39807 |
0,34611 |
0,64654 |
0,51556 |
0,43324 |
|
DF3 |
1,07812 |
0,46373 |
0,63423 |
1,48503 |
0,29893 |
0,31623 |
|
DF4 |
1,70829 |
0,2219 |
0,23465 |
3,21155 |
0,31159 |
0,30098 |
|
DF5 |
3,27418 |
2,86193 |
3,17044 |
3,54135 |
3,44858 |
3,16089 |
Окончание табл. 2
|
Медленные изменения |
||||||
|
Задача |
NSGA-2 |
SPEA2 |
||||
|
С рестартом |
Без рестарта |
Рестарт 50 % |
С рестартом |
Без рестарта |
Рестарт 50 % |
|
|
DF6 |
5,82266 |
4,37637 |
3,9914 |
7,65581 |
10,31912 |
6,58776 |
|
DF7 |
2,88988 |
0,21077 |
0,29967 |
0,57322 |
0,14004 |
0,16273 |
|
DF8 |
0,4861 |
0,24668 |
0,46732 |
0,36439 |
0,06035 |
0,07962 |
|
DF9 |
1,11271 |
1,00767 |
0,87972 |
1,00105 |
0,77221 |
0,35849 |
|
DF10 |
0,63374 |
0,20805 |
0,28913 |
0,80103 |
0,16978 |
0,2983 |
|
DF11 |
1,33799 |
1,20587 |
1,21676 |
1,52398 |
1,248 |
1,26458 |
|
DF13 |
1,14789 |
0,82343 |
0,92381 |
1,99445 |
0,92517 |
0,59001 |
|
DF14 |
1,96974 |
2,15505 |
2,46098 |
0,86397 |
0,24935 |
0,24797 |
|
Быстрые изменения |
||||||
|
Задача |
NSGA-2 |
SPEA2 |
||||
|
С рестартом |
Без рестарта |
Рестарт 50 % |
С рестартом |
Без рестарта |
Рестарт 50 % |
|
|
DF1 |
0,15418 |
0,37973 |
0,1188 |
0,34685 |
0,67789 |
0,23528 |
|
DF2 |
0,43164 |
0,7622 |
0,3886 |
0,67347 |
0,98689 |
0,53114 |
|
DF3 |
0,99878 |
0,8379 |
0,91423 |
1,4139 |
0,65215 |
0,59109 |
|
DF4 |
1,75676 |
0,19023 |
0,20557 |
3,34937 |
0,30802 |
0,31553 |
|
DF5 |
5,48928 |
5,47719 |
5,51248 |
5,78571 |
6,27579 |
6,03813 |
|
DF6 |
5,83975 |
15,35728 |
7,55838 |
7,94478 |
19,964 |
7,73518 |
|
DF7 |
3,71561 |
0,41029 |
0,66258 |
0,66013 |
1,09603 |
0,562 |
|
DF8 |
0,4835 |
0,25431 |
0,46186 |
0,35465 |
0,07659 |
0,08844 |
|
DF9 |
1,06701 |
1,91676 |
1,07585 |
0,99857 |
2,52754 |
0,94053 |
|
DF10 |
0,55375 |
0,19654 |
0,24747 |
0,6755 |
0,15305 |
0,23408 |
|
DF11 |
1,31739 |
1,21583 |
1,21464 |
1,51375 |
1,25063 |
1,2498 |
|
DF13 |
1,11659 |
1,03303 |
0,91568 |
2,01859 |
3,41013 |
1,16391 |
|
DF14 |
1.96235 |
2,78436 |
2,68979 |
0,85173 |
0,51699 |
0,4661 |
Таблица 3
|
Медленные изменения |
||||||
|
Задача |
NSGA-2 |
SPEA2 |
||||
|
С рестартом |
Без рестарта |
Рестарт 50% |
С рестартом |
Без рестарта |
Рестарт 50% |
|
|
DF1 |
1,32092 |
1,54591 |
1,53165 |
0,96699 |
1,24592 |
1,34441 |
|
DF2 |
1,15173 |
1,14765 |
1,2953 |
0,7926 |
0,96943 |
1,11871 |
|
DF3 |
0,37984 |
0,84905 |
0,72257 |
0,14168 |
1,09988 |
1,07317 |
|
DF4 |
4,05769 |
7,6282 |
7,58849 |
1,28999 |
7,3678 |
7,36317 |
|
DF5 |
137,27398 |
139,51692 |
138,1649 |
111,54741 |
113,28194 |
113,31316 |
|
DF6 |
0,18186 |
0,60413 |
0,61594 |
0,0376 |
0,21177 |
0,20861 |
|
DF7 |
0,60904 |
2,95476 |
2,64463 |
2,05972 |
3,08956 |
3,00454 |
|
DF8 |
0,82234 |
1,49508 |
0,94826 |
1,03271 |
1,73879 |
1,6861 |
|
DF9 |
0,20507 |
0,39313 |
0,37082 |
0,3858 |
0,88429 |
1,05993 |
|
DF10 |
1,37764 |
2,56913 |
2,39078 |
1,10203 |
2,6405 |
2,32359 |
|
DF11 |
0,30304 |
0,50691 |
0,49764 |
0,07836 |
0,44429 |
0,41238 |
|
DF13 |
7,55833 |
10,14608 |
8,68482 |
1,08663 |
3,19273 |
4,40662 |
|
DF14 |
0,0873 |
0,06332 |
0,09364 |
0,1999 |
0,75084 |
0,73419 |
|
Быстрые изменения |
||||||
|
Задача |
NSGA-2 |
SPEA2 |
||||
|
С рестартом |
Без рестарта |
Рестарт 50 % |
С рестартом |
Без рестарта |
Рестарт 50 % |
|
|
DF1 |
1,38279 |
1,07766 |
1,45141 |
1,02725 |
0,80304 |
1,22049 |
|
DF2 |
1,14435 |
0,70886 |
1,20913 |
0,75946 |
0,5301 |
0,95102 |
Окончание табл. 3
|
Задача |
NSGA-2 |
SPEA2 |
||||
|
С рестартом |
Без рестарта |
Рестарт 50% |
С рестартом |
Без рестарта |
Рестарт 50% |
|
|
DF3 |
0,43748 |
0,66908 |
0,60571 |
0,19885 |
0,19885 |
0,77118 |
|
DF4 |
3,37641 |
6,5282 |
6,4919 |
0,94274 |
6,24129 |
6,20666 |
|
DF5 |
294,16315 |
295,48085 |
295,87608 |
238,39456 |
236,6676 |
240,46001 |
|
DF6 |
0,17802 |
0,29026 |
0,28404 |
0,03593 |
0,07157 |
0,12937 |
|
DF7 |
0,97366 |
3,33281 |
2,84268 |
2,64918 |
3,08993 |
3,28456 |
|
DF8 |
0,85182 |
1,51224 |
0,9437 |
1,0689 |
1,74353 |
1,70175 |
|
DF9 |
0,24943 |
0,121 |
0,2484 |
0,40496 |
0,17604 |
0,45905 |
|
DF10 |
1,72413 |
2,72373 |
2,60652 |
1,4608 |
2,79819 |
2,55707 |
|
DF11 |
0,33402 |
0,53781 |
0,53404 |
0,08475 |
0,47655 |
0,45826 |
|
DF13 |
7,66373 |
9,09398 |
8,21799 |
1,11795 |
1,1479 |
2,48469 |
|
DF14 |
0,0907 |
0,04726 |
0,08153 |
0,2078 |
0,45549 |
0,44884 |
Из представленных в таблице результатов видно, что в случае медленных изменений при решении большинства тестовых задач использование популяции, полученной на предыдущем шаге, является наиболее эффективным. Однако в случае быстрых изменений можно увидеть увеличение количества задач, при решении которых использование рестарта (либо полного, либо 50 %) является наиболее эффективным. Это связано с тем, что при быстрых изменениях состояние задачи на предыдущем шаге отличается от состояния на текущем шаге в большей степени в сравнении с медленными изменениями.
На рис. 4 приведены диаграммы значений рангов, присвоенных значению метрики для каждого из шести вариантов алгоритма и суммированных по всем тестовым задачам. Для наилучшего значения метрики присваивался наивысший ранг. Для обеспечения достоверности ранжирования была проведена проверка значимости различий в результатах с использованием критерия Манна – Уитни: критерий применялся к паре рядом стоящих по рангу результатов. Если различия незначимы, то этим двум результатам присваивалось среднее значение их рангов. Видно, что существенного различия между использованием алгоритма NSGA-2 и SPEA2 не наблюдается.
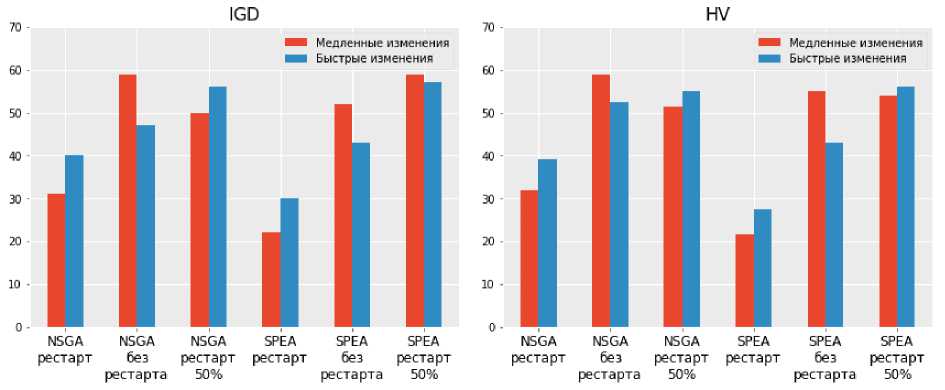
Рис. 4. Диаграммы значений суммарных рангов использованных алгоритмов
Fig. 4. Diagrams of the rank’s values of the algorithms
На рис. 5 и 6 на примере двух тестовых задач показаны графики изменения значения метрик IGD и HV на каждой итерации алгоритма NSGA-2 при медленных (сверху) и быстрых (снизу) изменениях. Можно увидеть, что каждые 30 итераций алгоритма происходит резкий скачок значений метрик – в этот момент возникает изменение в задаче.
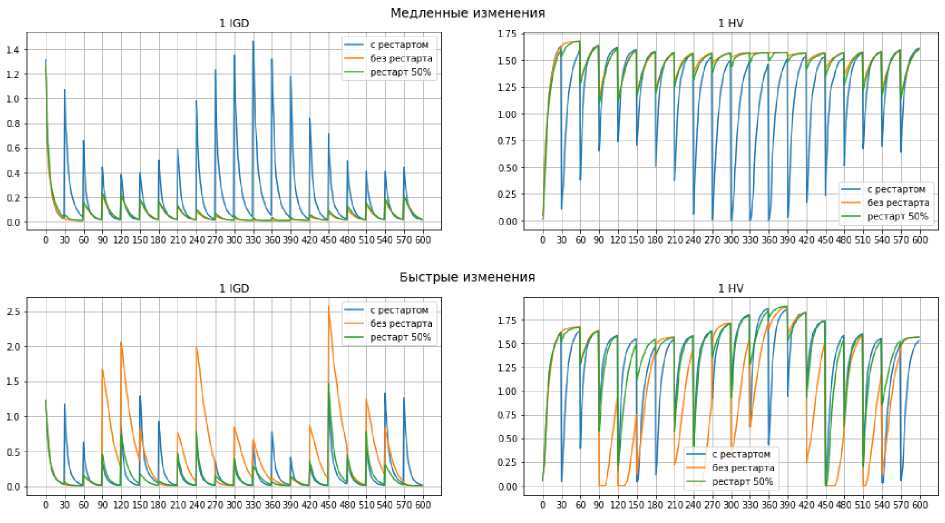
Рис. 5. Изменение значений метрик на примере задачи DF1 при медленных и быстрых изменениях
Fig. 5. Changing values of IGD and HV metrics in DF1 problem in the cases of slow and fast changes
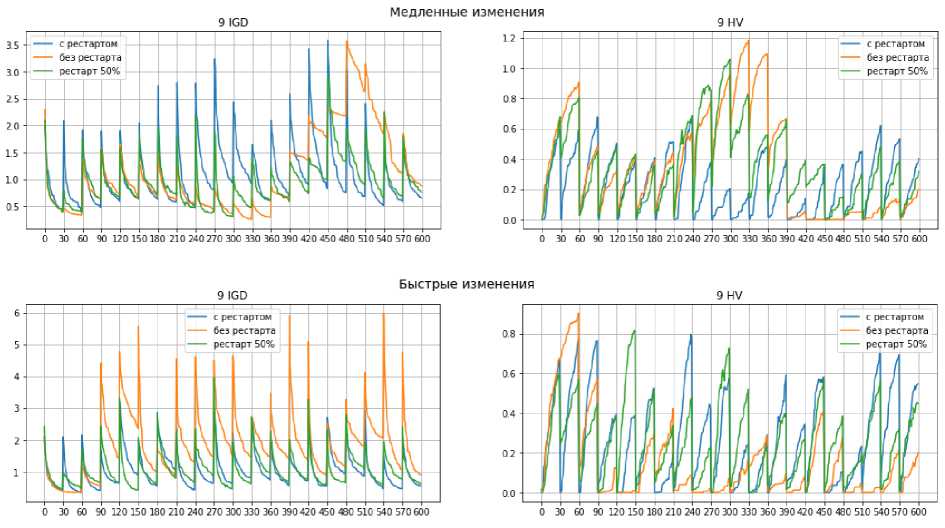
Рис. 6. Изменение значений метрик на примере задачи DF9 при медленных и быстрых изменениях
Fig. 6. Changing values of IGD and HV metrics in DF9 problem in the cases of slow and fast changes
При быстрых изменениях в задачах DF1 и DF9 можно увидеть, что при отсутствии рестарта значение ошибки при возникновении изменений гораздо выше в сравнении с использованием рестарта. Также в задаче DF9 при медленных изменениях видно, что на первых итерациях алгоритма при отсутствии рестарта наблюдается низкое значение ошибки, однако на последующих шагах алгоритма ошибка увеличивается. Это говорит о том, что в рамках одной задачи необходимо использовать разные подходы в зависимости от степени возникающих изменений.
Заключение
На наборе тестовых задач многокритериальной нестационарной оптимизации с использованием алгоритмов NSGA-2 и SPEA2 были рассмотрены три подхода к формированию популяции при возникновении изменений в задаче. Было показано, что эффективность использования популяции решений, полученных в предыдущий момент времени, зависит от скорости изменений в задаче.
При медленных изменениях на большинстве тестовых задач лучший результат показывает подход, который подразумевает использование популяции, состоящей только из решений, полученных в предыдущий момент времени, поскольку вид задачи изменяется незначительно. Однако при быстрых изменениях не представляется возможным выделить по предпочтительности какой-либо подход из трех возможных, поскольку все три подхода имеют примерно одинаковое соотношение тестовых задач, в которых их использование было наиболее эффективным. Из этого следует необходимость отслеживания интенсивности происходящих в задаче изменений, и на основе этой информации делать выбор в пользу того или иного подхода формирования популяции.
Список литературы Сравнение эффективности различных подходов к формированию популяции при решении задач многокритериальной нестационарной оптимизации
- Yazdani D., Cheng R. A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades-Part A // IEEE Transactions on Evolutionary Computation. 2021. No. 25(4). P. 609-629.
- Zhang J., Xing L. A Survey of Multiobjective Evolutionary Algorithms // 22017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC), 2017.
- Nguyen Т. Т., Yang S., Branke J. Evolutionary dynamic optimization: A survey of the state of the art // Swarm and Evolutionary Computation. 2012. No. 6. P. 1-24.
- Azzouz R., Bechikh S., Ben Said L. Dynamic Multi-objective Optimization Using Evolutionary Algorithms: A Survey. Adaptation, Learning, and Optimization. 2016, P. 31-70.
- Yazdani D., Cheng R. A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades-Part B. // IEEE Transactions on Evolutionary Computation. 2021. No. 25(4). P. 630-650.
- Li C., Yang S. A general framework of multipopulation methods with clustering in indetectable dynamic environments // IEEE Trans. Evol. Comput. 2012. No. 16(4). P. 556-577.
- Deb K., Karthik S. Dynamic multi-objective optimization and decision-making using modified NSGA-II: a case study on hydro-thermal power scheduling. Lecture Notes in Computer Science. 2007. P.803-817.
- Muruganantham A., Tan K., Vadakkepat P. Evolutionary dynamic multiobjective optimization via kalman filter prediction // IEEE Trans. Evol. Comput. 2016. No. 46(12). P. 2862-2873.
- Solving dynamic multi-objective problems with a new prediction-based optimization algorithm / Q. Zhang, S. Jiang, S. Yang, H. Song // PLoS ONE. 2021. No. 16(8).
- Branke J. Memory enhanced evolutionary algorithms for changing optimization problems. Proceedings of the 1999 congress on evolutionary computation, Institute of Electrical and Electronics Engineers, 1999.
- Goh C., Tan K. A competitive-cooperative coevolutionary paradigm for dynamic multiobjective optimization // IEEE Trans. Evol. Comput. 2009. No. 13(1). P. 103-127.
- Branke J., Kaussler Т., Smidt C., Schmeck H. A Multi-population approach to dynamic optimi-zaton problems. Evolutionary Design and Manufacture, Springer Science mathplus Business Media. 2000. P.299-307.
- Li C., Yang S. Fast Multi-Swarm Optimization for dynamic optimization problems. 2008 Fourth International conference on Natural Computation, Institute of Electrical and Electronics Engineers, 2008.
- Deb K., Pratap A., Agarwal S., Meyarivan T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II // Ieee transactions on evolutionary computation. 2002. No. 6 (2). P. 182-197.
- Zitzler E., Laumanns M., Thiele L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm. Computer Engineering and Networks Laboratory (TIK), Department of Electrical Engineering, Swiss Federal Institute of Technology (ETH), Zurich, 2001.
- Jiang S., Yang S., Yao X., Chen Tan K., Kaiser M. Benchmark Problems for CEC2018 Competition on Dynamic Multiobjective Optimisation. CEC2018 Competition, 2018.
- Zhang Q., Yang S., Wang R. Novel Prediction Strategies for Dynamic Multiobjective optimization. IEEE Trans. Evol. Comput. 2020, 24(2), P. 260-274.
- Rong M., Gong D., Pedrycz W., Wang L. A multimodel prediction method for dynamic mul-tiobejctive evolutionary optimization. IEEE Trans. Evol. Comput. 2020, No. 24(2), P. 290-304.


