Сравнение энергетических спектров сигналов акустической эмиссии по фрактальным размерностям и сравнительным диаграммам

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2025PNRPU MECHANICS BULLETIN

Сигналы акустической эмиссии (АЭ) генерируются при быстром изменении напряженного состояния (разгрузке) в отдельных областях нагруженного тела (металла, композита, горной породы) в результате произошедшей в них неупругой деформации посредством дислокационного сдвига, двойникования, мартенситного превращения, разрушения посредством образования или продвижения трещины, а также в результате распространения коррозии. Одной из первых работ, посвященных изучению АЭ, была работа А.Ф. Иоффе [1], в которой отмечена генерация звука при деформировании цинка и нагретой каменной соли. Первые систематические исследования АЭ были выполнены в докторской диссертации Д. Кайзера [2], основные результаты которой были опубликованы в работе [3]. В этих работах исследовалась АЭ в процессе растяжения, когда генерация звука была обнаружена при деформировании многих материалов. Автор констатировал, что «шумы необратимы, т.е. после напряжения определенного уровня шум возникает только тогда, когда тот же образец снова подвергается нагрузке, когда уровень первого напряжения превышен». Данный эффект сейчас называется эффектом Кайзера. Относительно недавние исследования показали, что эффект Кайзера изменяется при варьировании ориентации главных осей или (и) главных значений тензора напряжения [4].

Более подробно история развития науки о причинах АЭ, ее классификации, закономерностях, методах регистрации и последующего анализа изложена в учебном пособии Л.А. Оглезневой и А.Л. Калиниченко [5]. В настоящее время исследования АЭ применяются для решения многих прикладных и фундаментальных задач, среди которых фиксация факта и определение местоположения возникновения трещины, неразрушающий контроль состояния материала, в частности обнаружение состояния, предшествующего разрушению (для горных пород – землетрясению). Вопросы классификации, распространения, дисперсии, затухания и регистрации ультразвуковых волн изложены в учебном пособии [6]. Там же указано, что механизмы деформирования и разрушения материала при испытаниях определяют связь потока импульсов АЭ с параметрами нагружения и в конечном счете используются для обоснования критериев браковки.

В работе [7] установлено, что в осадочных породах при увеличении скорости деформации наблюдается АЭ-эффект, который заключается в росте интенсивности излучения в частотном диапазоне от сотен герц до первых десятков килогерц, наиболее сильно он проявляется на заключительной стадии подготовки землетрясений. Исследование АЭ при подвижках грунта смоделировано в работе А.А. Остапчука с соавт. [8]. В ней показано, что перед динамическими срывами наблюдается степенной рост количества акустических импульсах и микроподвижках, причем на стадии подготовки динамических срывов излучаются высокочастотные (30–80кГц) импульсы, а динамический срыв проявляется в виде низкочастотного (< 20 кГц) сигнала.

Пример комплексного использования акустических методов для наблюдения дефектов в углепластике – метода АЭ в сочетании с методом акустоупругости – приведен в работе [9]. Достоверность локации дефектов обеспечена методом АЭ, а определение деформаций основано на эффекте акустоупругости, заключающегося в зависимости скорости упругих волн Лэмба от деформации, что позволяет измерять напряжения по временам задержки упругих волн Лэмба.

Ввиду возможностей метод АЭ положен в основу ГОСТ Р 52727–2007 [10], в котором утверждается, что в основе метода АЭ (как метода неразрушающего контроля и технической диагностики) «лежит физическое явление излучения волн напряжений при быстрой локальной перестройке структуры материала» и что «источником акустико-эмиссионной энергии служит переменное поле упругих напряжений от развивающихся дефектов». В [10] отмечено, что «метод акустической эмиссии (АЭ) является чувствительным к любым видам структурных изменений в широком частотном диапазоне работы (обычно от 10 до 1000 кГц). Оборудование способно регистрировать не только хрупкий рост трещин, но также процессы развития локальной пластической деформации, затвердевания, кристаллизации, трения, ударов, течеобразований и фазовых переходов». Подробное изложение преимуществ и ограничений метода АЭ при решении производственных задач представлено в обзорной работе [11].

Получить непосредственную информацию о природе источников АЭ очень сложно ввиду искажений сигналов за счет отражений от свободных поверхностей образца, возбуждения разных типов волн, имеющих различные скорости распространения (продольных, поперечных, поверхностных волн Рэлея, волн Лэмба); искажений из-за дисперсии волн и из-за различного коэффициента затухания волн разной частоты; искажений, создаваемых датчиком, волноводом и усилителями электрических колебаний. Одним из путей является поиск информативных параметров АЭ, которые сохраняются при передаче и преобразовании сигналов. Исследователи рассматривают такие характеристики АЭ, как общее количество сигналов, их энергия, автокорреляционная функция, взаимная корреляционная функция, спектральная плотность мощности, медианная частота, а также ряд других характеристик [12; 13]. В работе [14] показано, что при статическом нагружении образцов из дюралюминия при низкой температуре –50 oС количество регистрируемых сигналов увеличивалось, но энергия высокочастотной составляющей сигналов АЭ уменьшалась. В этой же работе показано, что некоторые характеристики спектров сигналов, полученных с помощью преобразования Фурье или вейвлет-преобразования, позволяют определять начало разрушения, хотя сами спектры подвергаются искажениям. Среди других параметров для предсказания начала разрушения используют среднюю частоту и угол нарастания сигнала АЭ [15] и параметр разупорядоченности АЭ-данных [16].

График зависимости амплитуды сигнала от времени имеет сложную изломанную форму. Он может быть рассмотрен как фрактальная кривая, важнейшей характеристикой которой является фрактальная размерность. Идеи фрактальной и мультифрактальной геометрии, используемые при анализе АЭ, изложены в книге [17].

Расчет фрактальных размерностей был использован в работах [18–23]. В [18] изучены методы анализа сигналов АЭ, рассматриваемых как временные ряды, по которым строили множество d -мерных векторов и вычисляли его корреляционную размерность. Другой способ, использованный в этой работе, заключался в построении кумулятивных рядов для последовательностей времен наступления и энергий событий АЭ, для которых вычисляли корреляционные интегралы и корреляционную размерность. В работе [19] применен информационно-статистический подход для исследования временных рядов АЭ, в рамках которого найдены информационная энтропия, фрактальная размерность и параметр самоорганизации сигнала АЭ. Показано, что эти параметры имеют меньшие значения для области максимального упрочнения. Установлено, что уменьшение информационной энтропии и фрактальной размерности свидетельствует о снижении хаотичности сигнала АЭ. Аналогичный подход использован в работе [20], в которой последовательность сигналов АЭ характеризовали корреляционной фрактальной размерностью множества векторов, построенного по алгоритму Грассберга – Прокаччи [21]. Метод, основанный на изучении фрактальной размерности, для определения особенностей сигнала АЭ при влиянии на них шума предложен в работе [22]. В работах [23; 24] методика мультифрактального анализа использована для изучения сейсмических сигналов. Показано, что метод анализа флуктуаций после исключения масштабно-зависимых трендов может быть использован для изучения низкоэнергетических сейсмических сигналов перед, во время и после наступления сейсмических событий. Указано, что необходимо изучать динамику спектра сингулярности временного ряда, изменение которого может свидетельствовать об изменении характера исследуемых процессов, которое может быть невидимо как для традиционных методов, так и для фрактального анализа, основанного на расчёте только показателя Хёрста.

Другим способом анализа сигналов является поиск таких их характеристик, которые не изменяются под действием многих из перечисленных искажений. В данной работе рассмотрен способ анализа сигналов акустической эмиссии (АЭ), основанный на том обстоятельстве, что график энергетического спектра сигнала, имеющий сложную изломанную форму, может быть рассмотрен как фрактальная кривая, важнейшей характеристикой которой является фрактальная размерность. Эта характеристика изменяется при варьировании условий формирования сигналов и, следовательно, может служить характеристикой для классификации сигналов АЭ. Этот метод был использован для выявления изменений спектральных характеристик сигналов АЭ в результате испытаний на малоцикловую усталость.

Ввиду этих обстоятельств перспективным является сравнение характеристик сигналов, полученных на «свежих» образцах и образцах, испытавших различные механические (в частности циклические) воздействия. Разработка надежных способов сравнения открывает пути для оценки остаточного ресурса деталей для принятия решения о возможности их дальнейшего использования.

В работах [25; 26] на примере алюминиевых (сплав Д16) и стальных (стали 20, 45Х и 5Г17Ю3) образцов было показано, что в энергетических спектрах сигналов АЭ, полученных при индентировании металла после циклических испытаний, фиксируются характерные изменения по сравнению со спектрами сигналов от образцов в исходном состоянии. Во всех случаях «искажения» имели похожий характер: с увеличением количества циклов испытаний пики на кривой спектральной плотности энергии снижались и «раздваивались» в сторону увеличения частоты.

Оригинальный способ исследования эволюции энергетического спектра сигналов, генерируемых при деформировании образца, был реализован в работах [27; 28], в которых для анализа АЭ в процессе непрерывного деформирования образцов вводится параметр эволюции АЭ, равный интегралу по всем частотам от логарифмической производной по времени энергетического спектра сигнала. Таким образом, вычисляется относительное изменение спектра за малый интервал времени. В этих работах показано, что введенный параметр, во-первых, возрастает по модулю на ранних стадиях пластического течения и, во-вторых, мало зависит от характеристик широкополосного датчика, волновода и усилителя сигналов АЭ.

Аналогичная идея, использованная в настоящей работе, лежит в основе сравнения сигналов, полученных на одинаковых образцах до и после их испытаний. Она состоит в построении сравнительного спектра, представляющего собой отношение усредненных Фурье-образов сигналов. Если уравнения, описывающие генерацию, распространение и регистрацию сигналов, линейны, то это отношение равно отношению Фурье-образов сигналов до искажений, то есть в том виде, в каком они возникли внутри материала.

Методика анализа изменения спектра сигналов АЭ

Построение сравнительного спектра основано на предположении, что процессы генерации, распространения и регистрации сигналов описываются линейными уравнениями. Пусть w (t) - оригинальный сигнал, каким он порожден в материале, а x (t) - зарегистрированный сигнал, искаженный при прохождении по образцу и приеме датчиком. Тогда предполагаем, что функции w(t) и x(t) связаны уравнением

Lx ( t ) = w ( t ),                       (1)

где L - линейный дифференциальный оператор. Применяя к уравнению (1) преобразование Фурье, получим

B ( f )X ( f ) = W ( f )

или

X ( f ) = A ( f ) W ( f ),                (2)

где f - частота, W ( f ) и X ( f ) - Фурье-образы функций w ( t ) и x ( t ), а A ( f ) и B ( f ) - прямая и обратная передаточные функции. Оператор L и функции A ( f ) и B ( f ) зависят от условий распространения и регистрации сигналов. Кроме сигналов, генерируемых пластическими сдвигами или растрескиваниями, аппаратура записывает также шум различной природы.

Обозначим возмущение, создаваемое шумом, через w шум ( t ), а его спектр через W _шум ( f ). Если регистрируется только шум, то аппаратура покажет спектр X ш_ум .= AW шум . Если же регистрируется и сигнал, и шум, то спектр АЭ будет равен

X = X деф

^{+ X} шум

= A ( W деф + W шум ) ,

где нижний индекс «деф» обозначает, что АЭ порождена деформацией. Пусть с помощью одного и того же датчика получены сигналы от двух образцов (или от двух областей одного образца), спектры которых X 1 и X 2 . Тогда

X деф1 = ^X , - ^X шум = ^AW деф^^2 = ^X 2 - ^X шум = ^AW деф2 .

Построим сравнительный спектр W 21 двух сигналов в форме отношения

W =   ² ____ шум

²¹ " X 1 - X шум

AW * ² = ^W .

^AW^ ! ^W^

которое, хотя и не позволяет найти спектры W _деф₁ и W д_еф2 , но дает сравнительную информацию об этих сигналах, не зависящую от условий прохождения сигналов и параметров регистрирующей аппаратуры.

Характеристикой сигнала АЭ, которая не изменяется под действием искажений, вносимых волноводами и датчиком, возможно, является фрактальная размерность спектра. Если она зависит от условий формирования сигналов, то может быть использована для их классификации. График спектральной плотности энергии имеет сложную изломанную форму. Его фрагменты при уменьшении их размера не являются в точности подобными, поэтому данный график нельзя характеризовать только одной фрактальной размерностью то есть с точки зрения теории фракталов его следует классифицировать как мультифрактал. Кроме того, как все природные объекты, его фрактальный характер прослеживается только до определенных минимальных размеров, то есть он представляет собой предфрактал. В качестве примера рассмотрим график нормированной спектральной плотности энергии некоторого сигнала, заданной на дискретном наборе равноотстоящих частот (рис. 1). Будем рассматривать его как график плотности распределения частот, в котором нормированная энергия играет роль вероятности встретить данное значение частоты.

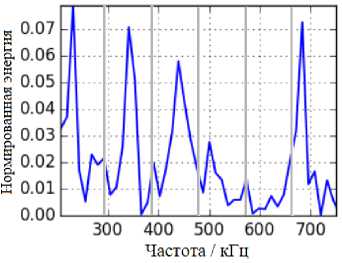
Рис. 1. Схема расчета фрактальной размерности спектральной плотности мощности сигнала АЭ. Вертикальные линии делят интервал значений энергии на N частей

Fig. 1. A scheme for calculating the fractal dimension of the spectral power density of the AE signal. Vertical lines divide the range of energy values into N parts

Выберем количество m отчетов частоты, входящих в один интервал разбиения всей области значений частоты. Таким образом, эта область оказывается разбита на N ( m ) интервалов. Найдем

D 1 ( m ) = 7-- — E N-m ) p log 2 Pi, log₂ m    ^{= 1}

где p – сумма значений энергии, соответствующей всем частотным отсчетом из -го частотного интервала. Если бы существовала возможность неограниченно увеличивать число интервалов разбиения, то величина D 1 = lim ( D 1 ( m ) ) представляла бы собой информацион- m ^^

ную фрактальную размерность графика спектральной плотности энергии. При конкретных вычислениях количество интервалов N ( m ) выбирали достаточно большим (соответственно m – достаточно малым). При этом оказывалось, что значения D 1 ( m ) слабо различаются при близких малых значениях m , так что величина D 1 ( m ) может служить оценкой информационной фрактальной размерности графика спектральной плотности энергии.

Для экспериментального исследования выбран образец из рулонной стали марки 20 (ГОСТ 10705), вырезанный из электросварной прямошовной трубы производства ТЭСЦ-3 ТЭСК МСД ОАО «Выксунский металлургический завод» диаметром 426 и толщиной стенки 7 мм, предел текучести σт = 360 МПа, сваренной токами высокой частоты. Образец был подвергнут циклическому нагружению: отнулевой цикл с максимальным напряжением σmax =1,2σт, частотой f = 20 Гц. Испытание прекратили на стадии формирования «шейки», видимой невооруженным глазом, в результате которого его относительное удлинение составило 15 %. При этом количество циклов равнялось 8851. Изучали сигналы АЭ, возникающие при внедрении в образец твердосплавного конического индентора со скоростью 1,0 мм/мин на испытательной машине ИМ-4А. Максимальная нагрузка на индентор составляла 1000 Н. Для регистрации и преобразования АЭ-сигналов в электрические применяли широкополосный датчик АЭ MSAE-L2 и усилитель MSAE-FA010 с общим усилением 87 дБ. Амплитудночастотная характеристика датчика со встроенным предусилителем характеризуется плавным снижением чувствительности от 92 дБ (по отношению к уровню 1 В/(м/с)) при 100 кГц до 65 дБ при 500 кГц. Внешний вид установки показан на рис. 2. Поверхность образцов очищали от окислов и шлифовали. Индентирование проводили вдоль всей длины образца. Для каждого укола сигналы АЭ с использованием методики цифрового распознавания и анализа спектров [29] разбивали на группы по форме кривой энергетического спектра и строили усредненные спектры по каждой группе. В данной работе для всех изученных образцов 95–100 % составляли сигналы со спектром одного вида, что свидетельствует о действии источников АЭ одного типа.

Рис. 2. Внешний вид установки: 1 – блок нагружения с коническим индентором; 2 – испытываемый образец;

3 – датчик АЭ

Fig. 2. The installation: 1 – loading unit with a conical indenter; 2 – test sample; 3 – AE sensor

Результаты анализа сигналов АЭ

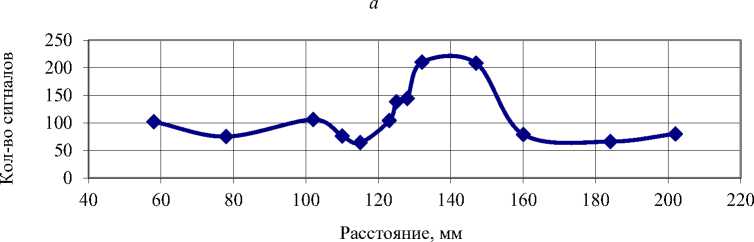
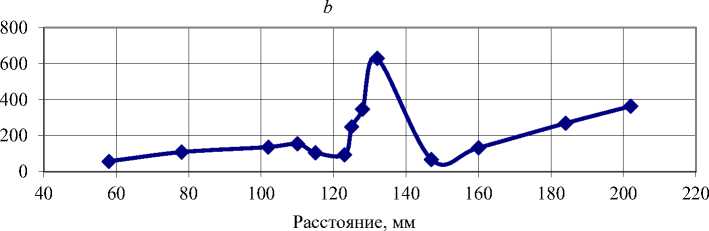
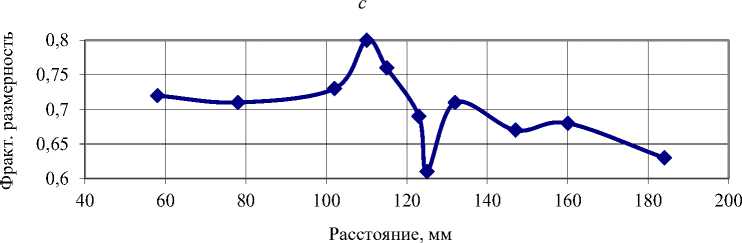
Инициирование АЭ осуществляли путём вдавливания твердосплавного конического индентора на испытательной машине ИМ-4А. Уколы производили в точках, распределенных вдоль оси образца от одной области захвата (недеформированный материал) через рабочую часть, включающую шейку, до области второго захвата. На рис. 3 приведена фотография рабочей части образца и сопоставленные с ней графики распределений параметров АЭ. Из данных рис. 3 видно, что такие характеристики АЭ, как количество сигналов, средняя энергия и информационная фрактальная размерность D1 усредненного энергетического спектра, имеют существенные отличия в области локализации деформации. Там регистрируется большее общее количество сигналов, энергия усредненного сигнала имеет большее значение, а фрактальная размерность среднего сигнала изменяется сложным образом, имея наименьшее значение в наиболее сильно деформированной области вблизи шейки. Таким образом, рассмотренные характеристики АЭ могут служить индикатором роста плотности дефектов.

Для оценки изменения характера АЭ после механических испытаний образца выполнили сравнение сигналов, полученных индентированием вблизи захвата, где состояние образца близко к исходному (точка 2 на рис. 3, а ), в рабочей части образца (точки 9 , 10 , 15 на рис. 3, а ) и вблизи шейки, там, где предварительная деформация наибольшая (точка 16 на рис. 3, а ). На рис. 4 показаны спектры сигналов, полученных при индентировании в различных точках образца, а также сравнительные диаграммы спектров.

d

Рис. 3. a – фотография образца после циклических испытаний. Параметры акустической эмиссии при индентировании образца в различных точках, распределенных по его длине: b – количество сигналов; c – энергия усредненного сигнала; d – фрактальная размерность спектра усредненного сигнала

Fig. 3. a – photo of the sample after cyclic testing. Acoustic emission parameters during sample indentation at various points distributed along its length: b – number of signals; c – energy of the mean signal; d – fractal dimension of spectrum of the mean signal

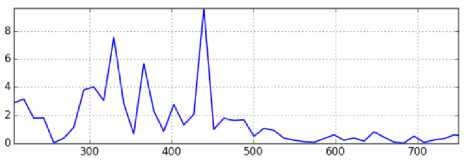
a – недеформированный материал (точка 2 )

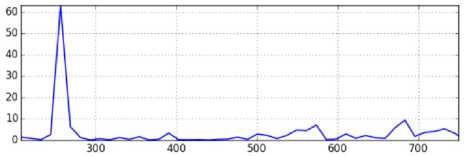
f – деформированный материал (точка 9 )

ООО b – деформированный материал (точка 9)

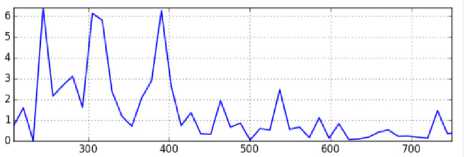
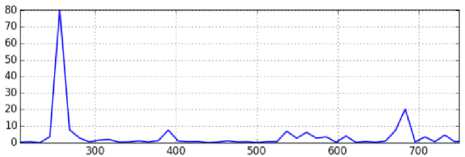
g – деформированный материал (точка 10 )

c – деформированный материал (точка 10 )

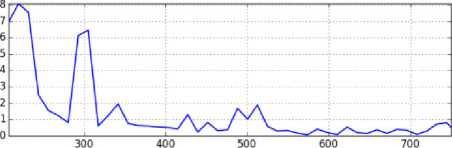
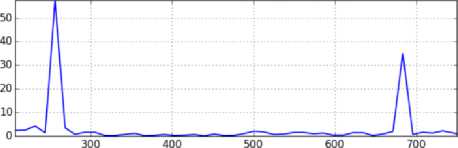
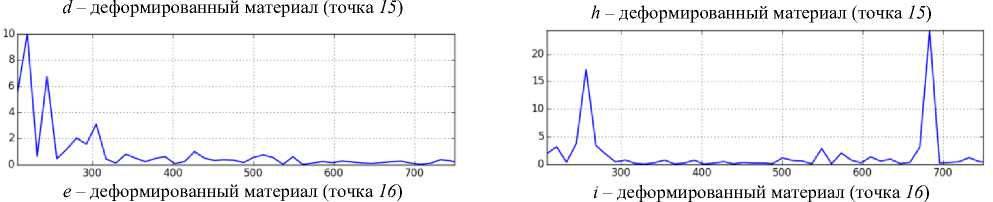
Рис. 4. a, b, c, d, e – спектральная плотность мощности АЭ-сигнала в точках 2, 9, 10, 15, 16 ; f, g, h, i – сравнительные диаграммы спектров сигналов от деформированного материала в точках 9, 10, 15, 16 с сигналом от недеформированного материала в точке 2

Fig.4. a, b, c, d, e spectral power density of the AE signal at points 2, 9, 10, 15, 16 ; f, g, h, i comparative diagrams of spectra signals from the deformed material at points 9, 10, 15, 16 with a signal from the undeformed material at point 2

Визуальное сравнение позволяет обнаружить изменения спектра сигнала, однако достаточно сложно явно сформулировать характер этих изменений. На сравнительных диаграммах различие сигналов видно более отчетливо. В частности, выделяется пик вблизи частоты 270 кГц, высота которого снижается по мере приближения к области шейки. Одновременно увеличивается высота пика, расположенного вблизи частоты 680 кГц. Сравнительная диаграмма не является спектром какого-либо сигнала, поэтому неясно, как можно объяснить имеющиеся на ней пики. Поскольку условия получения и регистрации сигналов АЭ на сравниваемых образцах одинаковые (одинаковые размеры образцов, один и тот же индентор, один и тот же датчик и его расположение относительно индентора, один и тот же усилитель электрической записи сигнала), то линейные искажения сиг- налов, вносимые этими факторами, согласно формуле (3), на сравнительную диаграмму не влияют. Таким образом, можно предположить, что пики на диаграммах, представленных на рис. 4 (f, g, h, i), связаны с изменениями в условиях генерации сигналов (плотности и расположения дефектов), произошедших в процессе циклического нагружения. При этом остается неясным, с чем связано появление пиков вблизи конкретных значений частот.

Из данных рис. 5 видно, что оценка фрактальной размерности в сильно деформированном материале равна 0,62 (при N ( m )=50), то есть меньше, чем в недеформиро-ванном (0,72). Измеренная в ходе выполненных экспериментов оценка фрактальной размерности шума (также при N ( m )=50) равнялась 0,86. Таким образом, снижение величины этого параметра может служить признаком уменьшения хаотичности сигнала.

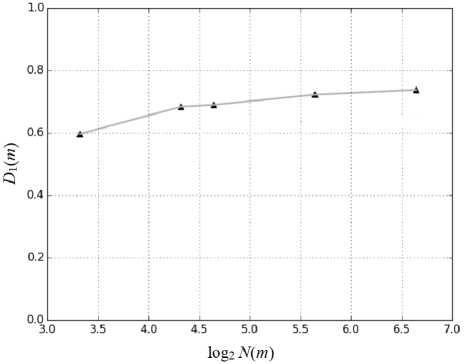
Рис. 5. Зависимости оценки информационной фрактальной размерности D 1 ( m ) спектра мощности сигнала от числа разбиения N ( m ) для сигналов, полученных при индентировании: a – недеформированного материала в точке 2 ; b – деформированного материала в точке 16

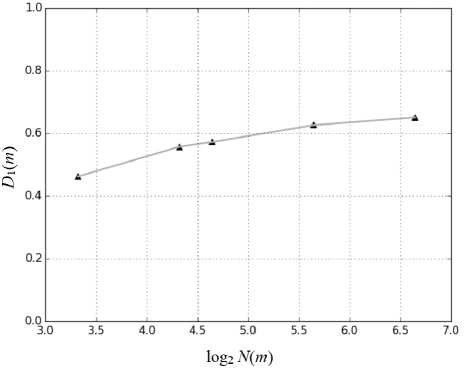
b

Fig. 5. Dependences of the estimate of the information fractal dimension D 1 ( m ) of the signal power spectrum on the number of partitions

N ( m ) for the signals obtained during indentation: a – undeformed material at point 2 ; b – deformed material at point 16

Заключение

Фрактальная размерность энергетического спектра сигнала акустической эмиссии зависит от деформационной истории материала. После значительной пластической деформации стали 20 фрактальная размерность снижается, что, по-видимому, означает уменьшение хаотизации