Сравнение квантово-химических моделей расчета спектроскопических свойств GeO

Развитие элементной базы промышленности, связанной с электроникой, микроэлектроникой, фотоникой, требует получения и использования чистых, особо чистых веществ, а также совершенных кристаллических материалов. Кристаллический германий используется в полупроводниковой электронике при изготовлении элементов микросхем, отдельных радиоэлектронных компонентов, в качестве фотоприемников, как детекторный материал для ионизирующих излучений [1, 2]. Германий широко применяют в инфракрасной оптике в качестве материала линз и окон, в акустооптике - при изготовлении модуляторов инфракрасного диапазона [3, 4]. Как подложечный и одновременно функциональный материал германий используют для производства солнечных элементов с высоким КПД [2].

В ряде случаев возможно использование кристаллов без особых требований к структуре (оптический германий), но высокую чистоту и совершенную структуру должен иметь детекторный германий, а подложки для фотоэлектрических преобразователей, в свою очередь, должны иметь низкую плотность структурных дефектов. Возникновение дефектов кристаллической структуры происходит по различным причинам, основная из которых тепловые условия выращивания (как следствие – термоупругие напряжения). Одновременно существенное влияние на получение бездислокационного германия и особочистого германия оказывает присутствие кислорода в растущем кристалле. Кислород в германии определяет динамику образования дислокаций, микродефектов, термодоноров, влияет на время жизни неравновесных носителей заряда; на кислородных облаках, активированных легирующей примесью, происходит рассеяние излучения [5-7].

Анализ состояния кислорода в кристаллическом германии и оценка его влияния на свойства материала представляет собой актуальную задачу. Решение данной задачи следует искать в виде построения сначала классической (феноменологической), а потом и квантовой моделей сорбции и десорбции кислорода кристаллами.

Корректное описание физических явлений должно опираться на некоторую основу в виде физико-математической модели. Постановка и проведение эксперимента по изучению поведения кислорода в германии - довольно сложная и затратная процедура [5-7]. Поэтому желательно, с одной стороны, предварять все предполагаемые измерения теоретическим прогнозом, а с другой – подтверждать возникающие в результате исследований гипотезы теоретическими (в том числе численными) построениями. Целью настоящей работы была как оценка частоты валентного колебания в газообразном GeO в различных квантово-химических моделях (набор метод/базис), так и калибровка этих квантово-химических моделей.

Анализ частоты валентного колебания и длины связи оксида германия

Моделирование термодинамических свойств веществ (температурный сдвиг энтальпии Н' ° - H 0 , температурный сдвиг свободной энергии Гиббса G ^ - H 0 , энтропия S ⁰, теплоемкость C p , энтальпия A f H и свободная энергия Гиббса A f G образования из простых веществ) в приближении разделения движений приводит к представлению этих свойств в виде суммы составляющих (вкладов). В таком формализме основную погрешность в итоговое значение свойства вносят электронное (полная электронная энергия) и колебательное движения.

Вклад последнего движения зависит от геометрического строения соединения, массы атомов, частот колебаний и температуры. Ранее нами было проведено сравнение ошибок различных квантово-химических наборов метод/базис при воспроизведении длины связи ( r (Ge-O)) в газообразном оксиде германия [8]. Молекула GeO была использована при калибровке моделей как наиболее простое кислородсодержащее соединение германия. Мы продолжили сопоставлять наиболее известные методы на примере расчета частоты валентного колебания связи ( ω (Ge-O)).

Отобранные из литературных источников частоты валентного колебания связи ω (Ge-O) сведены в табл. 1 и 2. Спектр газообразного оксида германия содержит большое количество линий, которые при повышении температуры сливаются в широкие полосы. Сложность спектра связана с присутствием в природных образцах GeO нескольких изотопов обоих веществ, и в большинстве расчетных спектров была использована комбинация ⁷⁴Ge¹⁶O, соответствующая природному изотопическому составу элементов.

Все рассмотренные нами теоретические частоты (табл. 2 и 3) были найдены в гармоническом приближении ( ω_harm ). Гармоническая частота также может быть получена и при рассмотрении экспериментальных спектров в рамках колебательной теории возмущений. В работе [9] ω_harm была положена равной 985.5 см ^–1. В связи с различием в моделях (гармонический осциллятор – расчет и ангармонический осциллятор – эксперимент) теоретическая ω harm не обязана совпадать с экспериментальной ( ω_exp ), в то же время близость ω_harm и ω_exp свидетельствует об адекватности выбранного метода. Как следует из табл. 2, наибольшее согласие с экспериментом показали методы CCSD(T), CISD, MP2 и B3LYP. Однако во многих случаях даже для этой простой молекулы расхождение составило до 60 и более см^–1.

Ранее [10] было показано, что с увеличением числа базисных функций ( n_bas ) длина валентной связи, как правило, уменьшается, а с улучшением учета межэлектронной корреляции увеличивается. Это ( r = f ( n bs ) ) неизбежно приводит к зависимости между размером базиса

Таблица 1. Экспериментальные частоты (волновые числа) GeO ( ω exp ) в разных агрегатных состояниях, см ^–1

Соединение	[9]	[9] 1	[14]	[15]	[16]	[17]	[18]	[19] 2	[19] 3	[20] 1	[21]	[22] 4	[23] 4
76 Ge 18 O			924						926				927
74 Ge 18 O			926					929	928	925			930
73 Ge 18 O			927
72 Ge 18 O			928					931	930	928			932
70 Ge 18 O			931					934	933	931			935
76 Ge 16 O			969					973	971				973
74 Ge 16 O	978	986	971	975,1	985,5			975	973	970			975
73 Ge 16 O			972					977	975
72 Ge 16 O		989	973					978	976	973			978
70 Ge 16 O		991	976					980	978	975			980
Ge16O 5				966		976	976				977	975.1	975.1

¹ ω _harm , ² в твердом Ar, ³ в твердом N₂, ⁴ твердый GeO, ⁵ смесь изотопов Ge.

Таблица 2. Теоретические гармонические частоты (волновые числа) GeO ( ω_harm ), см ^–1

Метод/базис	ω harm	Метод/базис	ω harm
HF/VTZ	1127 [24]	CCSD(T)/SDB-cc-pVTZ	925 [29]
HF/6-311G**	1141 [23]	CCSD(T)/cc-pVDZ-PP/RECP	930 [28]
HF/DZP	1143 [23]	CCSD(T)/SDB+CPP-pVTZ	931 [29]
HF/SVP	1148 [23]	CCSD(T)/SDB-cc-pVQZ	943 [29]
HF/DZP+f	1166 [23]	CCSD(T)/SDB+CPP-pVQZ	949 [29]
HF/SVP+f	1176 [23]	CCSD(T)/cc-pVTZ-PP/RECP	980 [28]
Dirac-Hartree-Fock/VTZ	1123 [24]	CCSD(T)/cc-pV5Z-DK	980 [28]
PT1/VTZ 1	1124 [24]	CCSD(T)/cc-pVQZ-PP/RECP	982 [28]
MP2/DZP	944 [23]	CCSD(T)/cc-pV5Z-PP/RECP	982 [28]
MP2/TZVP	944 [14]	CISD/O – 10s6pld/[3s3pld] Ge – 5s5p2d	982 [25]
MP2/6-311G**	953 [23]	B3LYP/6-311G*	993 [27]
MP2/SVP	957 [23]	B3LYP/DZP	1001 [23]
MP2/DZP+f	980 [23]	B3LYP/6-311G**	1006 [23]
MP2/SVP+f	997 [23]	B3LYP/SVP	1010 [23
B3LYP/6-311++G(d,p)	975 [17]	B3LYP/SVP	1010 [14]
B3LYP/6-311G	976 [26]	B3LYP/DZP+f	1018 [23]
B3LYP/6-311+G(2df, 2pd)	991 [26]	B3LYP/SVP+f	1030 [23]

¹ теория возмущений первого порядка.

и to harm при использовании одного и того же метода расчета¹ (табл. 2). Поэтому наши расчеты, собранные в табл. 3, были выполнены с разными функционалами DFT, но с одним и тем же декартовым базисом 6-311++G(3df,3pd) 6d 10f.

Оптимизация равновесного строения и поиск ω harm выполнены с помощью программ GAUSSIAN 09 [11]. Расчет гармонических частот to harm методами функционала плотности с базисом 6-311++G(3df,3pd) представлен в табл. 3. Выбор базиса обоснован в [10, 12]. Как следует из табл. 3, наиболее приемлемые результаты получены с функционалами mPW2PLYP, VSXC, XAlpha, SVWN и B3LYP. Расхождение составило не более 15 см^–1, что позволяет использовать найденные величины при расчетах термодинамических свойств газообразного GeO с удовлетворительной точностью [10].

Проведенное исследование (данная работа и [8]) дает возможность оценить применимость различных методов теории функционала плотности (в формализме Кона-Шема) к расчету геометрических и спектроскопических свойств GeO и выбрать среди них наиболее удовлетворяющий критерию согласия с экспериментом. Кроме того, это позволяет дать прогноз по расчету ω_harm на основании только геометрических параметров (модель Баджера [13]). Для этого нами была рассмотрена корреляции между to harm и r (Ge-O) и вычислены параметры линейной регрессии (1) «гармоническая частота-длина связи»:

ω harm = ρ r + b . (1)

Параметры (1) для полученной совокупности значений найдены дважды (рис. 1):

• а)    в общем случае (т.е. по данным наших табл. 2 и 3 и табл. 1-3 из [8]) ρ = -2751.37 см ^–1× Å ^–1 и b = 5486 см ^–1 ( r корр = -0.846),

• б)    только наши расчеты (наша табл. 3 и табл. 3 из [8]) ρ = -2511.33 см ^–1× Å ^–1 и b = 5094 см ^–1 ( r корр = -0.966).

Корреляция между длиной связи и частотой валентного колебания известна для многих соединений [13]. Как правило, эта зависимость обычно не является линейной, однако полученный нами коэффициент корреляции Пирсона ( r корр ) говорит о линейности ω harm = f ( r ). При этом указанная прямая проходит выше экспериментальной точки (на рисунке отмечена ромбом), т.е. используемые функционалы (в среднем) завышают либо ω harm , либо r (Ge-O). Так, подстановка в (1) экспериментальной длины r (Ge-O) = 1.625 Å приводит к ω_harm = 1015 см ^–1 и ω_harm = 1013 см ^–1 в случаях а) и б) соответственно.

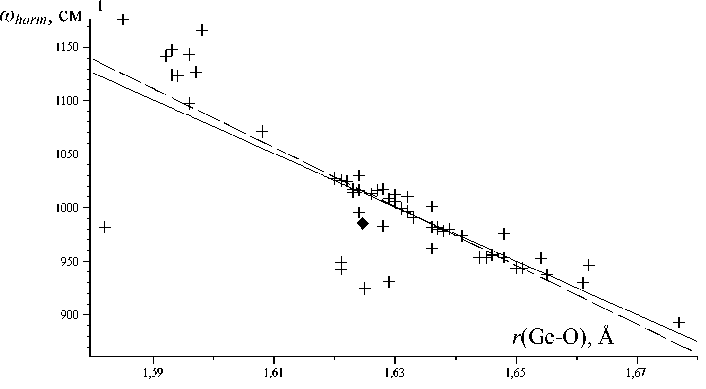
Рис. 1. Корреляционное поле и регрессии «гармоническая частота–длина связи». Сплошная линия построена по данным табл. 3, штриховая линия – по данным табл. 2 (см. в тексте). Ромбом отмечено экспериментальное значение

Таблица 3. Теоретические гармонические частоты (волновые числа) GeO ( ω harm ), см

Метод	ω harm	Метод	ω harm	Метод	ω harm	Метод	ω harm
HFB	893	VSXC	978	B972	1015	BHandHLYP	1071
BLYP	937	XAlpha	983	B98	1017	BHandH	1098
HFS	954	SVWN	996	B3P86	1017	UMP2-FC	947
B2PLYP	954	B3LYP	999	M06	1018	MP2(FULL)	954
BPW91	956	B1LYP	1009	PBE1PBE	1025
HCTH	962	B971	1012	MPW1PW91	1026
mPW2PLYP	974	B3PW91	1013	B1B95	1028	ωharm [11]	985,5

Если рассмотреть небольшую окрестность около экспериментальной точки (закрашенный черным ромб на рис. 1), то среди всех использованных моделей стоит выделить SVWN и XAlpha, которые удовлетворительно воспроизводят выбранные нами параметры и могут быть рекомендованы к расчету других свойств GeO. Большую погрешность к одновременному расчету реперных значений дают B972, B3PW91, B1LYP и B3P86. Однако сделанные предварительные выводы нуждаются в дополнительной проверке на геометрических и спектроскопических характеристиках других газообразных соединений германия (например, GeO2), а затем и при моделировании твердого тела.

Заключение

В работе проведена калибровка квантово-химических моделей по воспроизведению частоты валентного колебания и длины связи в газообразном оксиде германия. Наилучшее согласие с экспериментом и для частоты, и для длины связи показали функционалы SVWN, XAlpha, B972, B3PW91, B1LYP и B3P86, при этом если искать параметры по отдельности, то mPW2PLYP, VSXC, XAlpha, SVWN и B3LYP более точно воспроизводят частоту, а функционалы MB97-2, B972, B3LYP и LDA(SVWN), XAlpha. B3P86, B1B95, B1LYP, B98, B971, B3PW91, MPW1PW91, PBE1PBE, M06 – длину связи.

Авторы выражают благодарность Казанскому государственному технологическому университету за техническую поддержку при проведении расчетов.

Работа выполнена в рамках реализации ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы», соглашение 14.577.21.0004 (RFMEFI57714X0004).