Сравнение методов численного интегрирования в задаче дифракции плоской электромагнитной волны на прямоугольном отверстии

Во многих задачах о распространении лазерного излучения в среде возникает необходимость учета волновой природы света, в частности, это задачи дифракции, фокусировки лазерного излучения, оценки расходимости и др. Их решение основано на вычислении интеграла Гюйгенса–Френеля [1 –4]:

E p = k [ Em ^exp(~ ik ^P ) dS ,                    (1)

2Л S P где EP – амплитуда дифрагированной волны в точке наблюдения P, EM – амплитуда падающей волны в произвольной точке M волновой поверхности, k – модуль волнового вектора падающей волны, dS – площадь участка волновой поверхности, а ρ – абсолютная величина радиус-вектора от точки M до точки P.

Вычисление дифракционного интеграла – трудоемкая задача. Во-первых, подынтегральное выражение в нем представляет собой быстро осциллирующую функцию, что накладывает определенные требования как на выбор метода численного интегрирования, так и на шаг разбиения области интегрирования. Во-вторых, интеграл вычисляется по поверхности, площадь которой пропорциональна квадрату характерного размера пучка, а время, затрачиваемое на расчет, также пропорционально квадрату этого раз- мера и обратно пропорционально шагу разбиения. Большой шаг разбиения неизбежно приводит к большим погрешностям вычислений, а малый – к большим временным затратам. Поэтому выбор оптимального шага и метода численного интегрирования является весьма актуальной задачей.

Вопросам разработки, исследования, тестирования и применения численных методов приближенного вычисления определенных интегралов посвящено большое количество работ [5– 12].

Использование традиционных алгоритмов для вычисления интеграла от быстро осциллирующих функций подразумевает расчет по квадратурным формулам (метод прямоугольников, трапеций), что требует мелкого шага разбиения и приводит к значительным затратам вычислительных ресурсов [5–7].

Существуют и другие, более сложные и специализированные методы. Для интегралов от функций с фазой линейной формы часто используют метод Филона [6]. Он основан на построении составных квадратурных формул, в которых на каждом частичном интервале используется интерполяционный многочлен для амплитуды, и дальнейшее интегрирование выполняется точно.

Метод коллокаций Левина [9] предназначен для вычисления осциллирующих интегралов с более сложной фазовой функцией и может быть применим

для интеграла вида (1). Он заключается в переходе к решению обыкновенного дифференциального уравнения (ОДУ). Использование матрицы дифференцирования Чебышева позволяет далее свести задачу к решению системы линейных алгебраических уравнений (СЛАУ), чаще всего невырожденной. Основным недостатком данного метода является трудоемкость решения СЛАУ, поскольку получающаяся в результате матрица является плохо обусловленной, что может приводить к большой ошибке при получении решения. Тем не менее, во многих случаях использование метода коллокаций Левина позволяет получить более точный результат по сравнению с другими методами [13].

В данной работе приведены результаты сравнения стандартных квадратурных методов интегрирования дифракционного интеграла (1) в приближении Фраунгофера со специализированным методом коллокаций Левина и аналитическим решением на примере классической задачи дифракции плоской электромагнитной волны на прямоугольном отверстии в дальней зоне.

Аналитическое решение задачи дифракции плоской электромагнитной волны на прямоугольном отверстии в дальней зоне

Для сравнения методов численного интегрирования с точным аналитическим решением рассмотрим классическую задачу дифракции плоской электромагнитной волны на прямоугольном отверстии в дальней зоне. Ее решение подробно изложено, например, в [1 –2]. При нормальном падении плоской электромагнитной волны на прямоугольное отверстие шириной 2 a 0 и длиной 2 b 0 , лежащее в плоскости x y , а также разложении величины ρ по малому параметру теории дифракции и пренебрежении квадратичными членами по сравнению с линейными р = Z-(Xx + Yy )/ Z амплитуда дифрагированной волны E P в точке наблюдения P равна:

ikE₀ exp( - ikZ ) }      ikYy     a f      ikXx

E p ^— -- ^---- I exp^ ) dy I exp(     ) dx ,⁽²⁾

2 л     Z          Z ^j Z

- b                 - a о где (X, Y, Z) – координаты точки наблюдения P, (x, y, 0) – координаты произвольной точки М волновой поверхности.

Интегралы (2) легко вычисляются аналитически, и тогда амплитуда электромагнитной волны:

iE o 4 a о b о       .      . ( 2 a о X ) . Г 2 b о Y )

E p = ——^exP^{( - ikZ )sinc} l       I ^sinc l -ЛЛГ I - ⁽³⁾

A Z               \ A Z у \ A Z у

E P — Ah_x

sin

x h y

Здесь λ – длина электромагнитной волны.

Физической и измеряемой величиной является интенсивность света:

I P ^— I о X

^{4 a} о ^b о | A Z J

sinc2

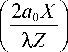
sinc2

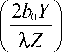
где I _о — c е _о E О2 /2 - интенсивность падающей волны, c -

скорость света в среде, ε 0 – электрическая постоянная.

Выражение (4) представляет собой аналитическое решение рассматриваемой задачи.

Построение численного решения с использованием стандартного квадратурного метода интегрирования

Рассмотрим построение решения интеграла (2) численным методом левых прямоугольников с постоянным шагом [5–6]:

b              N-1

Jf(x)dx = £f(j(j -xj) — h£f(xj, a                 j—1

где x j — a + ( j - 1 ) h , N — ( b - a ) / h .

Применяя (5) к выражению (2), получим:

E P — Ah_xh_y

N_x - 1

£ COS mx —1

N y - 1

£ cos my, —1

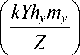
где

ikE 0

A —---- exp( - ik

2 л Z

( kXh x m x

I Z J

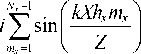
X

' Z + X (a о + hx) + Y (b о + hy)))

⁺ Z ⁺ Z I ¹

N_x — 2 a _о /h x + 1, N y — 2 b _о/ h y + 1.

Как известно [14]:

n            sin ( N a /2 ) - cos ( [ ( N + 1)/2 ] a )

£ cos (ja) —-----------— --------P jz1                       sin (a/2)

N

£ sin (ja) — j—1

sin ( N a /2 ) - sin ( [ ( N + 1)/2 ] a )

sin ( a /2 )

При подстановке (7) в (6) получим выражение для поля электромагнитной волны:

. ((Nx -1) kXhx) sin                c

I    2 Z    J

. ( kXh, sin

( 2 Z

Г ( N y - 1 ) kYh y

2 Z

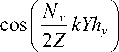
+ i

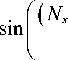
- 1 ) kXh_x

2 Z

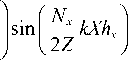
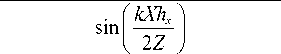
sin

Г kYh y ( 2 Z

Тогда аналитическое выражение для интенсивности, характеризующее решение рассматриваемой задачи численным методом левых прямоугольников:

I - 1 0

h x h y X Z

2 sin²

2 л a X ] . ₂1 2 л bY . _ I sin²1 „ _

X Z

sin2 —

I X Z

I X Z

. 2 ( л Yh sin²

( X Z

.

Как видно из решения (9), в окрестности точек:

n^x -л n , ^Л m™^? -л m , n , m - 1,2,...,         (10)

X Z       XZ

возникает неопределенность вида 0 / 0. Устраняя эту неопределенность, в пределе ε → 0 получим:

I - 1 0

h x h y

X Z

lim

sin2 {(Nx - 1)(лn + e)} sin2 (л n + e)

e^ 0

a x - a 0 /A x , a y - b 0/ A y и a x - ^a 0/ 6 A x , a y - ^ b 0/ 6 A y соответственно.

Формулы (13) представляют собой критерий для оценки шага интегрирования или количества узлов расчетной сетки в зависимости от размеров области наблюдения на экране и требуемой точности вычислений.

В табл. 1 приведена зависимость относительной погрешности ε i вычисления центрального и двух последующих максимумов в распределении интенсивности на одномерном экране от характерного параметра точности α x . Расчет приведен для следующих параметров задачи: интенсивность падающей волны I 0 =250 Вт / см², длина волны λ = 1 мкм, размеры пучка по оси х и y a 0 = b 0 = 1 см, расстояние от отверстия до экрана Z = 1 км, пределы наблюдения на экране X _max =20 см, Y _max =0 см.

sin2 {(Ny - 1)(лm + e)} sin2 (л m + e)

| 4 a 0 b 0 |

I .

01 X Z )

Формула (11) показывает, что значение интенсивности электромагнитной волны в точках ( X n , Y m ) существенно отличается от аналитического решения (4) и совпадает со значением для центрального максимума. В пределе h x → 0, h y → 0 формула (9) становится в точности равной аналитическому решению (4), которое не подразумевает наличие каких-либо максимумов вдали от центра экрана. То есть ( X n , Y m ) – координаты центров артефактных максимумов. Их возникновение в распределении интенсивности при численном интегрировании дифракционного интеграла методом левых прямоугольников неизбежно и связано с шагом интегрирования, а период определяется выражением:

A X - X n _{+ 1} - X n -X Z / h_x , A Y - Y_{m + 1} - Y_m -X Z / h y . (12)

Табл. 1. Зависимость относительной погрешности ε i от характерного параметра точности α x

α x , [–]	ε 0 , % ( Х =0 см)	ε 1 , % ( Х = 7,15 см)	ε 2 , % ( Х = 12,3 см)
0,3	4,66E-14	11,21	37,90
0,5	1,28E-13	4,81	15,05
0,8	1,16E-14	1,69	5,13
1,6	8,15E-14	0,42	1,25
8,0	6,75E-13	0,017	0,05

Если в заданных пределах области наблюдения на экране X max и Y max выполняются соотношения Δ X / X max < 1, Δ Y / Y max < 1, то метод левых прямоугольников неприменим для решения рассматриваемой задачи.

В связи с этим возникает необходимость введения ограничения на шаг интегрирования и количество узлов расчетной сетки:

hx -

Z 1

hy -

k^X max Z kY max

, N x - 1 + a x

a x

—, N y - 1 + a y a y

2 a 0 kX max

Z 2 b 0 kY max Z

,

.

где a x = f ( A x ), a y = f ( A y ) - характерные параметры точности, зависящие от заданной абсолютной погрешности квадратурного метода Δ x , Δ y , в частности, для метода левых прямоугольников и трапеций

Как видно из табл. 1, метод левых прямоугольников описывает центральный максимум в распределении интенсивности с точностью ~ 10 ^{– 13} %, которая практически не зависит от параметра α x . В то же время с увеличением α x погрешность вычисления интенсивности во втором и третьем максимумах уменьшается.

Таким образом, в заданных пределах области наблюдения на экране X max =20 см в точке Y =0 см для описания центрального и двух последующих максимумов в распределении интенсивности I ( X , 0) с погрешностью не более 2% характерный параметр точности должен составлять α x = 1,6, что соответствует N x =41 узлу расчетной сетки.

Построение численного решения методом коллокаций Левина

Рассмотрим решение поставленной задачи численного интегрирования выражения для электрического поля (2) специализированным методом коллокаций Левина. Как известно [9], данный метод приближенного вычисления интегралов от быстро осциллирующих функций основан на переходе к численному решению ОДУ с последующим сведением к СЛАУ для определения первообразной от подынтегральной функции p ( x ).

Функция p ( x ), удовлетворяющая условию:

4" [ P ( x )exp( i to g ( x )) ] - f ( x )exp( i to g ( x )), (14) dx

позволяет вычислить осциллирующий интеграл: Производную искомой функции dp / dx в дис- b jf(x)exP(i юg(x))dx -                          (15) - p (b) exp( i юg (b)) - p (a) exp( i юg (a)). кретном наборе точек [x0,…, xN] можно представить в виде: dp - Dp,                                   (17) dx Для определения функции p (x) достаточно удовлетворить уравнению: где p = [p (x0),...,p (Xn)]T D - матрица дифференцирования Чебышева. Элементы матрицы диффе- dp(x)     dg(x) я   +1ю Д   p(x) - f (x).                   (16) dx       dx ренцирования вычисляются по следующим формулам [15]: dj,k - ^1)—j, 0 < j # k < N, dk,k --1 -t^., 0 < k < N, d0,0 -1 (1 + 2N2), tj tk                                    2 1 tk                            6

d NN -- 1 ( 1 + 2 N ² ) , d 0, k - 2⁽—⁾ — , 0 <  k <  N , d k, 0 -- ^{1( z 1}^, 0 <  k <  N , 6                      1 - t k                        2 1 - t_k

d k , n - ^1(-^, 0 <  k <  N , d N , k - ^-( - ^ N ², 0 <  k <  N , d 0, N - ¹ ( - 1 ) N , d N ,0 -- ¹ ( - 1 ) N , 2 1 + t k                             1 + t k                        2                  2

где tj - cos(n/' / N), 0 < j < N - система узлов Гаусса–Лобатто.

Так как интеграл рассматривается на отрезке [ a , b ], то для перехода к стандартной области задания полиномов Чебышева [–1, 1] необходимо провести соответствующие преобразования переменных:

b-a b + a „ _ . __ xj - -y tj+ у, 0 < J < N.

Таким образом, при подстановке (17), (18) и (19) в уравнение (16) получим СЛАУ следующего вида:

(D + iюЛ) p - f,(20)

где

Л - diag

P ^- [ P ⁽ x 0 ),..., P ⁽ x N )f , f ^- [ f ⁽ x 0 ),..., f ⁽ x N ) ] T , b - adg ( x ₀ )    b - adg ( x_N )

2 dx 2 dx

Дифференциальная матрица D является сингулярной матрицей, но ее число обусловленности Cond( D ) = || D || || D ^–1|| улучшается при прибавлении к D диагональной матрицы i ωΛ. В этом случае || i ωΛ|| 2 показывает степень улучшения. Когда || i ωΛ|| 2 сравнительно велико, матрица ( D + i ωΛ) становится хорошо обусловленной Cond( D + i ωΛ) ~ 1, в противном случае она остается плохо обусловленной Cond( D + i ωΛ) >> 1, что ведет к большой ошибке при решении СЛАУ (20).

Применительно к рассматриваемой задаче с учетом (19) выражение (15) окончательно примет вид (21):

bb-a 1 drb - a j f (x) exp( i юg (x)) dx - —— j — [ p (x) exp( i юg (x))] dx - —— [ p (x0) exp( 1 юg (x 0)) - p ( Xn ) exp( 1 юg ( Xn ))].

a                           2 -1dX2

Тогда выражение (2) для амплитуды электромагнитной волны будет иметь вид:

ikE0a0b0 exp(-ikZ)             x0X

E p ^- — ------ p 1 ^{( x} 0 ) ^exP^{( ik} "^) ^- p 1 ^{( X} n ) ^exP^{( ik} ——)

2k     Z              ZZ p2(y0)exp(ik^ZY)- p2(yN )exp(ik^ZY) . (22)

Нетрудно заметить, что в окрестности точки X = Y =0 матрица ( D + i ωΛ) ≈ D , а значит, решение, полученное методом коллокаций Левина, может приводить к большой ошибке в распределении интенсивности вблизи центра экрана, поэтому возникает необходимость в выборе подходящего метода решения плохо обусловленной СЛАУ (20). В работе [13] отмечено, что надежным для решения данного типа задач является метод SVD (singular value decomposition), который и будет использоваться в дальнейшем.

Сравнение методов численного интегрирования с точным решением

Для сравнения двух квадратурных методов численного интегрирования (методы левых прямоуголь- ников и трапеций), а также специализированного метода коллокаций Левина с точным аналитическим решением (4) были выбраны следующие параметры задачи: интенсивность падающей волны I0 =250 Вт / см2, длина волны λ = 1 мкм, размеры пучка по оси x и y a0 = b0 = 1 см, расстояние от отверстия до одномерного экрана Z = 1 км, пределы области наблюдения на экране Xmax =20 см, Ymax=0 см.

На рис. 1 представлены графики зависимости интенсивности электромагнитной волны I от координаты Х на экране при Y =0 см, полученные в результате численного расчета методами левых прямоугольников, трапеций и коллокаций Левина, а также точное аналитическое решение. Численные расчеты квадратурными методами проводились на равномерной сетке с характерным параметром точности αx = 0,16, а специализированным методом – на сетке узлов Гаус-са–Лобатто. Количество узлов расчетной сетки во всех случаях составляло Nх =5. Для решения СЛАУ (20) применялся метод SVD.

I.Bm/cM2

О

• -20 -15 -10 -5    0    5   10   15 Х.см

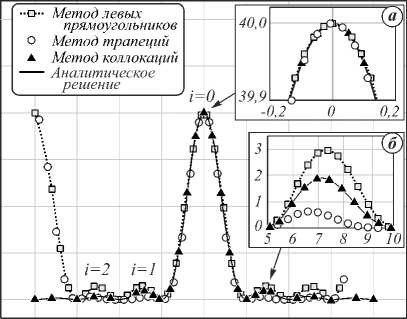
Рис. 1. Сравнение приближенного численного и точного аналитического решения: центральный максимум в увеличенном масштабе (а); второй максимум в увеличенном масштабе (б)

Из рис. 1 а , б видно хорошее качественное совпадение рассмотренных методов приближенного численного интегрирования с точным аналитическим решением при описании центрального максимума. Метод коллокаций Левина дает более точный результат при описании второго и третьего максимума в распределении интенсивности. Метод левых прямоугольников при этом завышает результат, а метод трапеций – занижает. Также из данных, представленных на рис. 1, виден артефактный максимум в распределении интенсивности, координата которого в соответствии с выбранными параметрами расчета совпадает с периодом Δ X =20 см.

В табл. 2 приведены результаты сравнения методов численного интегрирования по относительной погрешности ε i для центрального и двух последующих максимумов в распределении интенсивности. Количество узлов расчетной сетки во всех случаях составляло N х =41.

Табл. 2. Cравнение методов численного интегрирования по относительной погрешности ε i

Метод численного интегрирования	ε 0 , % ( Х =0 см)	ε 1 , % ( Х =7,15 см)	ε 2 , % ( Х =12,3 см)
Левых прямоугольников	8,15E–14	0,42	1,25
Трапеций	8,15E–14	0,84	2,48
Коллокаций Левина	2,68E–13	4,32E–13	3,75E – 13

Из табл. 2 видно, что на расчетной сетке, состоящей из Nx =41 узла, все рассмотренные методы количественно описывают центральный максимум с точ- ностью ~ 10 –13 %. Квадратурные методы оказываются в ≈ 3 раза точнее метода коллокаций Левина. Второй и третий максимумы при численном интегрировании методом коллокаций Левина описываются с точностью ~ 10 –13 %. В то же время максимальная погрешность вычислений методами левых прямоугольников и трапеций не превышает 3 %.

На рис. 2 показан график зависимости интенсивности I во втором максимуме с координатой Х = 7,15 см при Y =0 см от количества узлов расчетной сетки N x для трех методов численного интегрирования.

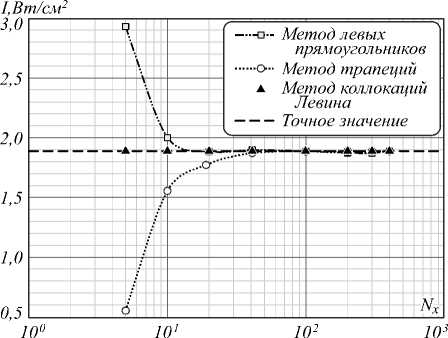
Рис. 2. Исследование методов численного интегрирования на сходимость

Из рис. 2 видно, что специализированный метод коллокаций Левина обладает наилучшей сходимостью и позволяет получать решение поставленной задачи уже на сетке, состоящей из N x ≈ 5 узлов. В то же время для описания второго максимума в распределении интенсивности стандартными квадратурными методами численного интегрирования с погрешностью не более 1 % потребуется сетка из N x ≈ 40 узлов.

На рис. 3 представлена зависимость отношения времени t , затрачиваемого на расчет различными методами, ко времени t ЛП , затрачиваемому на расчет методом левых прямоугольников от количества узлов расчетной сетки N x .

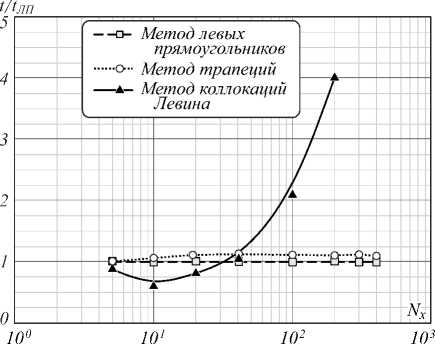
Рис. 3. Сравнение методов численного интегрирования по времени расчёта

Из данных, представленных на рис. 3, видно, что по временным затратам метод коллокаций Левина не уступает квадратурным методам вплоть до N x ≈ 40 узлов расчетной сетки. При N x >40 точек преимуществом по времени расчета обладают стандартные квадратурные методы численного интегрирования.

Заключение

На примере классической задачи дифракции плоской электромагнитной волны на прямоугольном отверстии в дальней зоне проведено сравнение трех алгоритмов численного интегрирования: метод левых прямоугольников, метод трапеций и специализированный метод коллокаций Левина.

Для квадратурных методов численного интегрирования получен критерий, определяющий выбор шага интегрирования в зависимости от размеров области наблюдения на экране и требуемой точности вычислений.

Показано, что для описания центрального и двух последующих максимумов в распределении интенсивности излучения на экране с погрешностью не более 2% метод коллокаций Левина требует ≈ в 8 раз меньшее количество узлов расчетной сетки по сравнению с методами левых прямоугольников и трапеций и не уступает им по временным затратам вплоть до N x ≈ 40 узлов. При N x >40 точек преимуществом по времени расчета обладают стандартные квадратурные методы численного интегрирования.

Таким образом, на примере решения задачи дифракции плоской электромагнитной волны на прямоугольном отверстии в дальней зоне показаны преимущества использования специализированного метода коллокаций Левина над стандартными квадратурными методами численного интегрирования.