Сравнение методов моделирования заводнения с учетом развития техногенных трещин средствами стандартных пакетов гидродинамического моделирования

Для вовлечения дополнительных запасов и рентабельной разработки месторождений с низкими фильтрационно-емкостными свойствами требуется проведение интенсификации добычи нефти уже на начальной стадии разработки. Одним из наиболее эффективных способов увеличения добычи является гидравлический разрыв пласта (ГРП). Одновременно с этим для поддержания пластового давления (компенсации отборов) используется технология заводнения пласта, в результате чего нефть вытесняется нагнетаемой водой под давлением [1]. Часто для достижения 100% компенсации отборов жидкости нагнетание воды производится при давлениях, превышающих давление разрыва породы, что приводит к значительному увеличению приемистости нагнетательных скважин. Данный факт связывают с образованием техногенной трещины (или системы трещин) в районе нагнетательной скважины [2], что в свою очередь приводит к эллиптическому фронту нагнетания. Для расчета технологических показателей разработки месторождений (уровней добычи жидкости, нефти и воды, уровней закачки и т.п.) все чаще используются гидродинамические модели. Однако как эффект от гидравлического разрыва пласта на добывающем фонде, так и развитие техногенных трещин на нагнетательном моделируются обычно скин-фактором, без учета геометрии и направления трещин.

Существует 2 основных момента, на которые необходимо обратить внимание при моделировании процесса заводнения с техногенными трещинами: задание давления разрыва/развития

техногенной трещины и использование в расчетах зависимости приемистости от давления нагнетания. Аналитически давление разрыва породы на нагнетательных скважинах можно получить, используя различные методики и корреляции, базирующиеся на результатах операций ГРП на добывающем фонде скважин и учитывающие в себе механические аспекты породы, термо- и пороупругие эффекты [3]. С теоретическим обоснованием зависимости приемистости от забойного давления, превышающего давление разрыва, дело обстоит не так очевидно. Автором был найден только один приближенный метод [4], основанный на интегральных законах сохранения энергии, выраженный формулой [1]:

_ P ₄ = X 64 khE'R Л Р  Q

= Д     h4     ch (Q"‘),      m где 5Р = Рзаб - Pf - перепад давления на трещине, Па; Рзаб - забойное давление, Па; Pf - давление в трещине, Па; ЛР = Pf - Рпл - репрессия на пласт, Па; Рпл - пластовое давление на контуре питания, Па; Q = Q^2nkh(ЛР) - безразмерный расход жидкости, Q - полный расход жидкости, м3/сек; ц - вязкость жидкости, Па^с; E' -плоский модуль Юнга, Па; h - мощность пласта, м; k - эффективная проницаемость, м2; R - радиус контура питания, м. Как утверждается в работе [4] расчеты по выше указанной формуле хорошо согласуются с промысловыми данными.

Для наиболее точного экспериментального определения давления разрыва используют так называемый метод пошаговой закачки (Step Rate Test). Суть его заключается в последовательном (пошаговом) увеличении скорости закачки жидкости в скважину и ожидания на каждом этапе стабилизации давления на забое (рис. 1,а). В отличие от записи индикаторной кривой метод пошаговой закачки – это исследование на неус-тановившихся режимах фильтрации. Кроме давления разрыва метод позволяет оценить такие параметры как среднее пластовое давление на контуре питания (рис. 1,б), проницаемость, скин и самое главное зависимость приемистости нагнетательной скважины от забойного давления. Тем самым для выбора оптимального метода моделирования заводнения при давлениях выше давления разрыва будем использовать критерий согласованности между результатами моделирования и теоретической зависимостью (1) или интерпретацией фактического исследования методом пошаговой закачки (рис. 1,б).

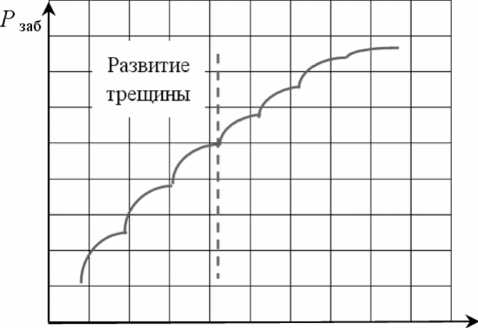
Время

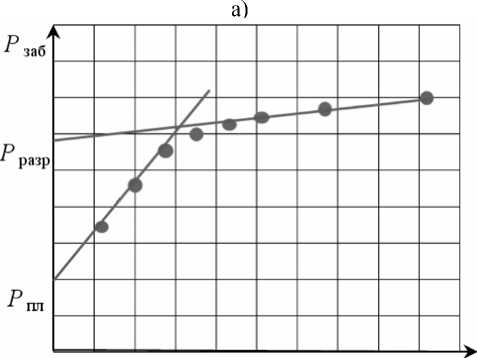
Приемистость

б)

Рис. 1. Метод пошаговой закачки: а) процедура проведения; б) интерпретация

К рассмотрению предлагается 3 способа учета развития техногенных трещин в гидродинамических моделях с помощью стандартных средств Eclipse. Сравнение проводилось на трехмерной секторной модели с пятиточечной системой расположения скважин. В тесте нагнетательная скважина работала на режиме управления по давлению, согласно схеме рис. 1,а. По результатам расчетов строились зависимости забойного давления от приемистости.

Первый способ: трещина моделировалась заданием повышенных проницаемостей ( k_x ^тр и k_y ^тр ) сеточных блоков, расположенных симметрично относительно нагнетательной скважины (рис. 2,а), рассчитанных по формулам:

к ? =

А х

Ах - w w kx      kfr

« к

" к Тр = (^ - w)ky + wkfr y            Ах        ’ (2)

где А х - размер ячейки, в нашем случае 20 м; w - средняя ширина трещины [3], k_fr = n w ² /64 -проницаемость трещины [5], k_x и k_y – проницаемости ячейки в перпендикулярном и параллельном направлениях трещины.

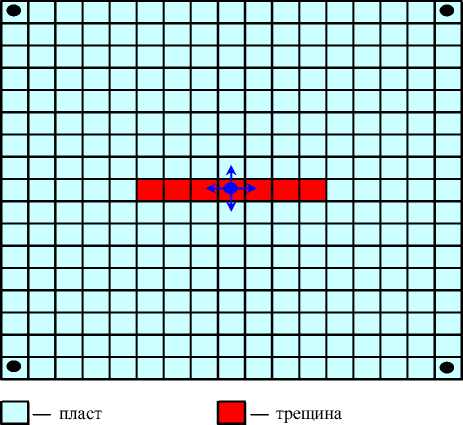
доб. скв.

нагн. скв.

а)

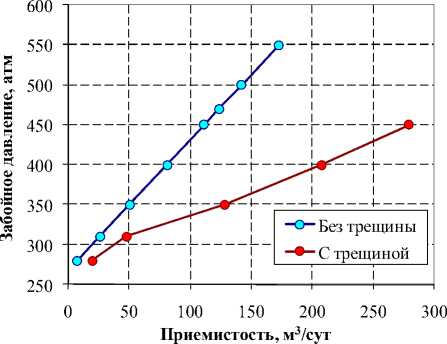
б)

Рис. 2. Прямой метод: а) модель трещины; б) зависимость забойного давления от закачки

Ориентация сетки каркаса должна совпадать с направлением развития трещины, которое в свою очередь может быть оценено обобщением проведенных исследований на месторождении (анализ кернового материала, тектонических условий региона, индикаторных исследований, результатов записи широкополосного акустического каротажа до и после операций ГРП на добывающем фонде, анализ динамики технологических показателей работы скважин). В результате наклон кривой приемистости относительно невозмущенного случая (рис. 2,б) становится положе (рост коэффициента приемистости). Отсутствие среди параметров модели давления разрыва породы является очевидным недостатком применения явного способа моделирования трещины. Также нет связи длины трещины с забойным давлением, т.е. исключена возможность согласованного развития техногенной трещины.

Второй подход – это увеличение коэффициента приемистости при давлениях выше давления разрыва с помощью ключевого слова WINJMULT, основными параметрами которого являются непосредственно давление разрыва и градиент увеличения подвижности (коэффициента приемистости). На каждом шаге происходит расчет мобильности флюида с дополнительным поправочным коэффициентом J:

J = 1

' 1 + ^{a ( Р}заб - ^Рразр } ^Рзаб ^ ^Рразр ,

1              P <  P

,                           ¹ заб разр ^,          (3)

где а -градиент увеличения подвижности (в нашем случае 0,1); P_разр – давление разрыва.

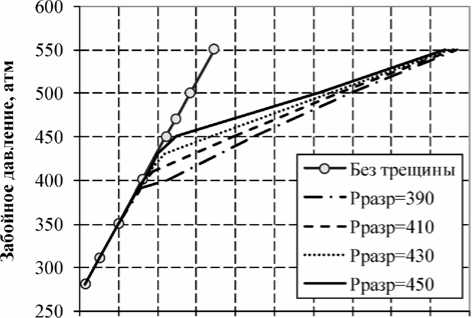
Анализируя вид кривых (рис. 3,а), полученных при различных давлениях разрыва, видно, что все кривые при росте забойного давления выходят на асимптоту. Предполагаем, что асимптотика связана с размерами ячеек, соединяющихся со скважиной, т.к. с ростом давления нагнетания проводимость этих ячейках растет, обеспечивая стремление всех кривых к одному значению. Достоинствами способа являются наличие среди параметров давления разрыва породы и возможность согласованного увеличения коэффициента приемистости. Недостатком остается отсутствие связи длины трещины с забойным давлением, что приводит к радиальному (неэллиптическому) оттоку от скважины.

Третий способ моделирования с учетом развития техногенной трещины связан с изменением проницаемости пласта в отдельных ячейках в зависимости от давления с помощью команды ROCKTAB. Этот метод сочетает в себе два предыдущих: выделение региона с возможным развитием трещины как на рис. 2,а, и переопределение проницаемости k_y ^тр ( k_x ^тр не изменяется (2)) в этом регионе по формуле:

^ 7 = 1

y , заб разр

Р 1^ у ,   заб — ¹ разр ,

0 где k_y

– начальная проницаемость ячейки; kyтр – модифицированная проницаемость ячейки, в1 -поправочный коэффициент, который может быть получен из формулы (2).

О 50 100 150 200 250 300 350 400 450 500

Приемистость, м3/сут

а)

О 50 100 150 200 250 300 350 400 450 500

Приемистость, м³/сут б)

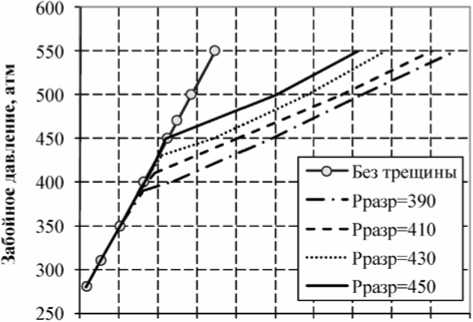
Рис. 3. Результаты расчета при разных давлениях разрыва с использованием команды: а) WINJMULT; б) ROCKTAB

По сравнению с предыдущими подходами применение команды ROCKTAB представляется наиболее физически обоснованным, учитывающим как давление разрыва, так и возможный рост техногенной трещины. Из рис. 3,б видно, что данный подход хорошо согласуется с видом интерпретации метода пошаговой закачки.

Выводы: рассмотрены основные подходы к гидродинмическому моделированию процесса заводнения с учетом развития техногенных трещин. Показано, что результаты реализованные подходом с изменением проницаемости в зависимости от давления нагнетания наиболее точно повторяют теоретические зависимости. Важно понимать, что корректное моделирование процесса заводнения при давлениях выше давления разрыва позволит правильно планировать и оптимизировать систему разработки месторождений.