Сравнение моделей с нейронной сетью и OLS-регрессией при построении стратегии управления риском от дохода по индексу

Введение.

Базовая структура сети проста: входной вектор из шести переменных и одномерный выход (переменная VWNY). Способность сети к обобщению может быть увеличена за счет прямых связей входных и выходных элементов [1–3]. Цель работы заключается в раскрытии перспективных эвристических подходов к оценке динамики функциональных связей в нейронной сети.

Если отсутствуют готовые схемы для оптимального выбора модели, необходимо апробировать различные критерии согласия. Для этого необходимо сравнить величины квадратного корня из среднеквадратичной ошибки (переменная RMSE) на тестовом множестве. После этого была задействована архитектура сети, которая выдавала наименьшую среднеквадратичную ошибку (табл. 1).

Т а б л и ц а 1

T a b l e 1

Квадратичный корень из средней квадратичной ошибки на подтверждающем множестве для обученных сетей различной архитектуры

Square root of the mean square root error on affirmative set for the trained networks of various architecture

Конфигурация / Configuration	Прямые связи / Direct links	Эпохи / Periods	RMSE
Коэффициент обучения / Learning factor – 0,93
6-2-1	Нет / No	29 000	0,12240
6-3-1	Нет / No	7 000	0,11090
6-5-4-1	Нет / No	1 800	0,11567
Коэффициент обучения / Learning factor – 2,00
6-3-1	Есть / Yes	22 300	0,10530

0,145

0,140

0,135

0,120

0,130

0,125

Обучение, коэффициент = 0,9 /

Learning, factor = 0,9

0,115

0,110

Тестирование, коэффициент = 0,9 / Testing, factor = 0,9

0,105

0,100

—I------------L___________I____________|| ।

2 500     5 000     7 500    10 000    12 500    15 000

Количество эпох / Number of periods

17 500

Р и с. 1. Квадратный корень из среднеквадратичной ошибки для 6-3-1

F i g. 1. Square root of the mean square root error for 6-3-1 network сети

Материалы и методы

Материалами для исследования послужили модели с непрерывной сетью

[4–7] и OLS-регрессия в пространстве стратегий управления от доходов, а также математическая статистика [8–10].

Результаты исследования

Рассматриваемый алгоритм включал в 2 раза больше эпох по сравнению с тем, в котором было достигнуто наилучшее обобщение. Таким образом, количество эпох было в 2 раза больше, чем показано в табл. 1 и рис. 1. При любом коэффициенте обучения RMSE на тестовом множестве будет меньше, чем на обучающем. Данный эффект мож- но объяснить зашумленностью обучаемого множества и отсутствием шума в тестовом множестве. Поскольку обучение прекращалось, как только значение RMSE начинало увеличиваться, можно предположить, что сеть не переобучилась, т. е. не «запомнила» шум. Таким образом, наличие больших погрешностей на обучаемом множестве объяснялось только белым шумом (рис. 1–3).

0,145

0,140

0,135

0,130

2c:

0,125

0,120 H

0,115 к

0,110

Обучение, коэффициент = 2,0 /

Learning, factor = 2,0

Тестирование, коэффициент = 2,0 / Testing, factor = 2,0

0,105

0,100

—1-------------1-------------1--1_____________।__i_____________।

2 500     5 000     7 500    10 000    12 500    15 000   17 500

Количество эпох / Number of periods

Р и с. 2. Квадратный корень из среднеквадратичной ошибки для 6-3-1 сети с коэффициентом обучения 2

F i g. 2. Square root of the mean square root error for 6-3-1 network with learning factor 2

Среди всех полученных нейронных сетей наилучшей является сеть с архитектурой 6-3-1 с прямыми связями и коэффициентом обучения 0,9. Для того чтобы получить решение в кратчайшие сроки, коэффициент обучения был увеличен в 2 раза. Шаги в направлении градиента значительно увеличились, вследствие чего произошло перескакивание через решение. В связи с этим для оптимального обучения сети понадобится намного большее количество эпох (~ 22 тыс.).

На рис. 1 показано, что RMSE убывает в первых 500 эпохах, а после 12 тыс. начинает колебаться. На рис. 3 представлены оценки, полученные на подтверждающем множестве с помощью OLS-регрессии и сети 6-3-1. Показания, которые вывела сеть, оказались как по значениям RMSE, так и по коэффициенту корреляции Пирсона. Однако на новых образцах данных сеть показывает лучшие результаты, чем на обучающем множестве (REG1).

До этого момента сравнивались архитектуры сетей и предполагалось влияние сигнала на результат. В связи с этим возникает вопрос: влияют ли данные переменные на конечный результат (табл. 2–3).

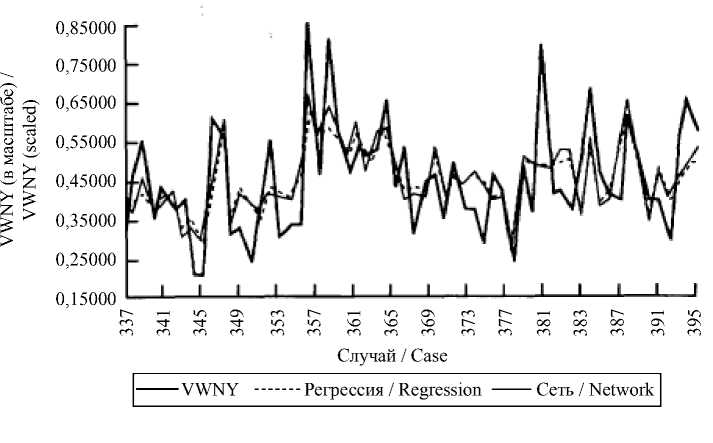
Р и с. 3. Сравнение значений переменной VWNY, полученных регрессией и сетью, с ее истинными значениями

F i g. 3. Comparison of VWNY variable values obtained by the regression and the network, with its true values

Т а б л и ц а 2

T a b l e 2

Критерии согласования для выходов регрессии и сети Concordance criteria for regression and network outputs

RMSE на обучающем и тестовом множестве / RMSE on learning and testing set
	REG1	REG2	Сеть / Network
Обучение / Learning	0,1210	0,1234	0,1189
Тестирование / Testing	–	0,1100	0,1030
Корреляция Пирсона / Pearson correlation
	VWNY	Регрессия / Regression	Сеть / Network
VWNY	1,00	–	–
Регрессия / Regression	0,66**	1,00	–
Сеть / Network	0,68**	0,98**	1,00

Примечание: ** – при 1%-ных хвостах распределения / Note: ** – in case of 1 % distribution tail areas

Т а б л и ц а 3

T a b l e 3

Для того чтобы оценить реальный вклад переменных в результат анализа нейронной сети, необходимо вычислить выход сети с оптимальным вектором. Предположим, что значение каждой переменной неизвестно и должно быть заменено на среднее арифметическое остальных пяти при их постоянных значениях. Таким образом были получены шесть новых входных матриц. После этого вычислялись выходные ряды для полученных входных матриц. Для данных рядов вычислили RMSE и сравнили ее с RMSE исходной входной матрицы. Дело в том, что если переменная активно влияет на решение, то ее RMSE будет значительно больше, чем в исходной матрице. Все найденные среднеквадратичные ошибки оказались больше исходных, а следовательно, замена переменной ее безусловным ожиданием только ухуд-

шает оценку целевой переменной. По результатам регрессионного анализа эти переменные квалифицируются как неактивные. Непредвиденная инфляция и месячная продукция имеют некоторое объясняющее значение и не могут быть заменены комбинациями других входных переменных.

При таком положении вещей различия между нейронной сетью и OLS-регрессией становится просто огромными. Чтобы улучшить результат за счет функции активации OLS-регрессии, можно использовать формулу:

R = дисперсия остатков (нелинейная модель) _, дисперсия остатков (линейная модель)

Значение данной функции лежит в промежутке между 0 и 1. Из-за того, что нейронные сети улавливают нели-

Вклад переменных в решение на обучающем множестве, тестовых множествах и всех данных

The contribution of all variables into the solution based on learning, testing sets and overall data

RMSE DC631 Ui(t) DEI(t) URP(t) UTS(t) MP(t + 1) YP(t + 12) Общее /Gen 0,117 0,118 0,120 0,141 0,148 0,117 0,119 Обучающее / Learn 0,119 0,120 0,123 0,143 0,139 0,119 0,121 Тестовое / Test 0,105 0,106 0,108 0,128 0,191 0,106 0,108 Разница в RMSE, % / Difference in RMSE, % Общее / Gen 100,00 0,94 2,88 20,30 26,45 0,33 1,74 Обучающее / Learn 100,00 0,91 2,87 20,02 16,54 0,26 1,51 Тестовое / Test 100,00 1,19 2,95 22,27 82,91 0,82 3,39 нейности в содержащихся данных, погрешность может только уменьшиться. Значения этих отношений оказываются примерно равными 0,94 и 0,92. Следовательно, либо в данных отсу-ствует нелинейность, либо нейронная сеть недостаточно эффективно использует свои нелинейные возможности. Предположим, что нелинейность в данных отсутствует, поскольку база данных строится с помощью линейных моделей. Большое значение данного отношения можно объяснить тем, что нейронная сеть лишь незначительно превосходит OLS-регрессию по критерию RMSE. Однако стоит заметить, что нейронные сети все же превосходят OLS-регрессию даже в работе с такими данными, в которых очень слабо выражена нелинейность между входами и целевой переменной.

Обсуждение и заключения

Нейронные сети имеют преимущество перед более традиционными методами в тех случаях, когда точное описание всех имеющихся взаимосвязей невозможно, но выделяется некоторый набор показателей, характеризующих исследуемое явление. В отсутствие четкой концептуальной модели применение регрессионных методов не представляется возможным. Данные по макроэкономическим факторам, использованные после предварительной

обработки оказываются почти идеально связанными с целевой переменной (доходом на NYSE) линейными связями, на что указывают большие значения коэффициента смешанной корреляции при регрессионном анализе и отношения R.

Выбранная архитектура сети с непосредственными связями между входами и выходами для такой ситуации является довольно удачной.Однако стоит отметить, что даже в сложной ситуации MBPN-сеть может превосходить метод OLS-регрессии по показателю RMSE и коэффициенту корреляции Пирсона. Более того, 6-3-1 сеть даже при работе с новыми данными позволяет составить более точный прогноз, чем оценка регрессии на уже ранее обработанных данных. Очевидна высокая степень согласованности результатов, касающихся вклада отдельных переменных, которые дают обычная регрессия и многослойная сеть. Такое соответствие повышает уверенность в правильности результатов и одновременно говорит о том, что, по крайней мере, линейная составляющая связи между доходом по индексу и выбранным фактором улавливается нейронной сетью достаточно успешно. Таким образом, работа нейронных сетей обретает большую прозрачность.

Все авторы прочитали и одобрили окончательный вариант рукописи.

Submitted 27.10.2016; revised 25.01.2017; published online 31.03.2017

All authors have read and approved the final manuscript.