Сравнение моделей вероятного кода числа PNC и циклического избыточного кода CRC

В настоящее время существует тенденция развития энергосберегающих технологий. Известно, что большой объем вычислений приводит к существенным затратам энергии. В результате актуальными являются исследования по снижению вычислительной сложности моделирования обработки данных. В сетях передачи данных важным показателем является достоверность и корректность входящих и исходящих потоков данных.

Турдиев Одилжан Акрамович аспирант Петербургского государственного университета путей сообщения Императора Александра I, Санкт-Петербург. Сфера научных интересов: вычислительная техника и сети в отрасли, моделирование информационных систем, программирование. Автор 10 опубликованных научных работ.

Существует много моделей и методик кодирования кодов, например, CRC, для контроля и формирования передаваемых данных с помощью добавления контрольных сумм к пакетам данных. Эти модели позволяют обнаружить ошибки, обработать полученные и отправленные данные в целях обеспечения достоверности.

Несмотря на то, что модель CRC широко используется, для нее по-прежнему сложно определить подходящие многочлены. Определение их характеристик становится очень сложным и критически важным для передачи информации в сетях, в которых необходимо обмениваться множеством данных с минимальными остаточными вероятностными ошибками. Эта задача решается с помощью детерминированных и стохастических методов [1].

Для обнаружения и исправления ошибок было разработано несколько методов коммуникации, например, Blahut (2003) [2]; Mac Williams and Sloane (1991) [3]; Суини (1991) [4]. Целью коммуникации, критически важной для безопасности, является обнаружение ошибок и инициирование перехода всего процесса в безопасное состояние, например, МЭК 61508 (2007) [5]. Это состояние не всегда является нормальным, но может быть причиной ограничения функциональности (например, состояние низкой скорости или нулевое напряжение).

Кроме того, в реальных условиях передачи на канал связи могут воздействовать различного рода помехи, проявляющиеся в исследуемом процессе в виде ошибочных бит, которые приводят к нарушению целостности данных [6]. В работе В.В. Яковлева [7] пред-

Сравнение моделей вероятного кода числа PNC и циклического избыточного кода CRC ложен выбор порождающего полинома для увеличения вероятности распознавание ошибок при формировании контрольных сумм в передаваемых данных.

Создание высококачественных, быстродействующих и достаточно простых алгоритмов формирования контрольных сумм с помощью параллельного генератора случайных чисел является одной из основных задач организации передачи данных с помощью низкочастотных энергосберегающих систем. От решения этой задачи в конечном счете зависит успех построения модели вероятного кода числа PNC (Probable Number Code), так как характеристики параллельного генератора случайных чисел (далее – ПГСЧ) во многом определяют параметры PNC.

Характеристика модели формирования контрольных сумм PNC

Передача данных – важная функция системы сети каналов передачи данных. Система передачи данных отправляет данные на обработку с помощью таких устройств, как программируемые логические контроллеры (далее – ПЛК), а ПЛК отправляют данные получателям. Важным является вопрос обеспечения целостности передаваемых данных, что делает его одним из самых важных функций низкой вычислительной сложности без уменьшения уровня обнаружения ошибки [7–9].

Актуальность вопроса синтеза вероятного кода числа PNC тесно связана с актуальностью задачи реализации принципов вероятностных методов моделирования и вычислений контрольных сумм данных, передаваемых по каналам связи.

На Рисунке 1 представлена модель структуры формирования PNC.

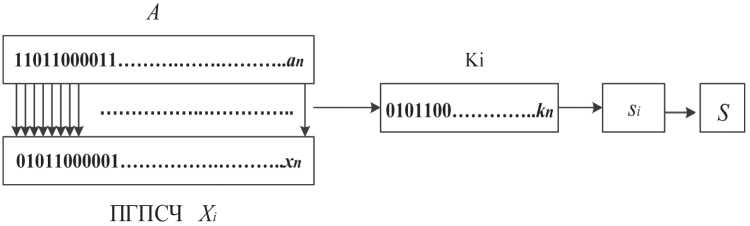
Рисунок 1. Пример структуры формирования PNC

Вычисление контрольной суммы для двоичной последовательности

A = (a1, a 2, a 3,..., an ), al ^{ 0;1}, осуществляется при помощи нескольких параллельных генераторов псевдослучайных чисел (далее - ПГПСЧ). С помощью i-го (i е{1,...,M}) ПГПСЧ генерируется случайная последовательность

Xi =(xi,1,xi,2,xi,3,...,xi,n), xi,j e{0;1}, je{1,-",n}, при этом x1,j = 1. Элементы последовательностей Xi с элементами последовательности A подвергаются логической операция «И» по mod 2 (обозначается символом &); в результате получаются следующие двоичные последовательности:

ki _, j= (a j & xi _, j )mod2 .

Элемент контрольной суммы получается с помощью K_i :

^ n

Si = I ki , j

A mod2 .

V

j=1

V

Таким образом, контрольная сумма представляет собой двоичную последовательность ^S (s i , s i , s i ,..., s M ) ,

где М – это число используемых ПГПСЧ.

Все эти действия можно представить в матричной форме следующим образом. Эле- менты xi,j формируют матритцу

X =

x1,1   x1,2

V x m ,1    x m ,2

^x1,n A

X^

2, n

X m , n у

Здесь X – это матрица ПГПСЧ; xi,j – случайное равномерно распределенное целое число, принимающее значения из множества {0; 1}, однако первая строка этой матрицы состоит только из единиц.

Элементы a_j формируют вектор

^ a 1 a

A =

a ₂

V an V

На линии передатчика вычисляется следующая сумма: матрица x _mn умножаются на a _n – вектор (исходной код), в результате получается сумма по каждой строке, s _m и S – контрольная сумма (PNC),

( s i

s =

s ₂

^a 1 Y ^{x i,} 1 a 2     ^x 2,1

x 1,2

x 2,2

x ¹ '' x ² , n

.

V s m V  V a n Y x m ,1   x m ,2

у

Если передаваемые A и S получили помехи и сбои, то имеем в приемнике A и S ,

^-

s = A ■ X

Чтобы обнаружить помехи и сбои, нужно сравнивать S – проверочный код с S : если

S ^ S , не равно есть ошибка, если равно - нет ошибки.

Пример с A = 11010, PNC = 5 показан на Рисунке 2.

1101010000 = A + S

Также это действие можно представить следующей формулой:

S[nА] = A[m■ n]■ X[nА].

Пример с вероятными помехами показан на Рисунке 3. 01010 10100

01010 00111

Сравнение моделей вероятного кода числа PNC и циклического избыточного кода CRC

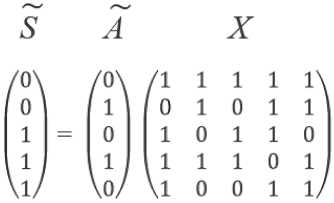
Рисунок 3. Пример вычисления с ошибками (помехами) PNC

Основные понятия модели формирования контрольных сумм CRC

Метод контрольного суммирования CRC основывается на свойствах деления с остатком многочлена (двоичное число). По сути результатом CRC является остаток деления многочлена, соответствующего исходным данным, на порождающий многочлен фиксированной длины.

Стандартный способ представления генераторного многочлена состоит в том, чтобы показать те позиции, на которых двоичные единицы являются степенями X . Примеры порождающих многочленов, используемых на практике, выглядят следующим образом [10]:

CRC 16 = x ¹⁶ + x ¹⁵ + x ² + 1

CRC - CCITT = x¹⁶ + x ¹⁵ + x ⁵ + 1

CRC 32 = x ³² + x ²⁶ + x ²³ + x ¹⁶ + x ¹² + x ¹¹ + x ¹⁰ + x ⁸ + x ⁷ + x ⁵ + x⁴ + x ² + x + 1 .

Следовательно, CRC-16 в двоичной форме эквивалентен записи 11000000000000101.

При таком генераторном многочлене до генерации FCS будет добавлено 16 нулей. Последний будет 16-битным остатком.

CRC-16 и CRC-CCITT широко используются в таких сетях, как ISDN, тогда как CRC-32 используется в большинстве локальных сетей. Метод CRC можно легко реализовать в аппаратном и программном обеспечении.

Один набор контрольных цифр генерируется (вычисляется) для каждого переданного кадра на основе содержимого фрейма и добавляется передатчиком к хвосту кадра. Затем приемник выполняет аналогичное вычисление по полному фрейму плюс контрольные цифры. Если ошибки не были найдены, всегда должен быть получен известный результат; если получен другой ответ, это указывает на ошибку.

Количество контрольных цифр на кадр выбирается в соответствии с ожидаемым типом ошибок передачи; наиболее часто встречаются 16 и 32 бита. Вычисленные контрольные цифры обозначаются как последовательность проверки кадров FCS (Frame Check

Sequence) или циклической избыточности CRC.

По существу метод использует свойство двоичных чисел. При использовании арифметики по модулю 2 [11]

M ( x ) - k - разрядное число (сообщение, которое должно быть передано);

G ( x ) - ( n + 1 ) - битное число (делитель или генератор);

R ( x ) - n - разрядное число такое, что k ^ n (остаток).

M ^{( x} )*2 " = q ( x ) + R ( x ) ,

G ( x )             G ( x )

где Q ( x ) является частным;

M ( x )*2 n + R ( x ) G ( x )

= а ( x ) ,

предполагая арифметику по модулю 2.

Этот результат можно легко подтвердить, подставив выражение для M(x) *2n G(x) во второе уравнение

M(x)*2n + R(x) = Q (x. + R(x) + R(x) G(x)                 G(x) G(x) , равное Q. (x), так как все добавленные к нему числа по модулю 2 будут равны нулю, то есть остаток будет равен нулю.

Чтобы использовать полное содержимое кадра M (x) вместе с добавленным набором нулей, равным по количеству FCS, которые должны быть сгенерированы (то есть умно- женные на 2n, где n - количеств FCS), разделены по модулю 2 на двоичное число ( G (x) – генераторный многочлен, содержащий на одну единицу больше, чем FCS). Операция деления эквивалентна выполнению операции «исключающее ИЛИ» по параллельному биту, так как обрабатывается каждый бит в кадре. Тогда остаток R (x) является FCS, который передается в хвосте информационных кадров.

Аналогично при получении принятый поток битов, включающий в себя число CRC, снова делится на один и тот же генераторный многочлен, то есть M ( x ) *2 n + R ( x )/ G ( x ) , и если ошибок нет, остаток – все нули. Однако если присутствует ошибка, остаток не равен нулю.

Выбор генераторного многочлена важен, поскольку он определяет типы обнаруженных ошибок. Предположим, что переданный кадр

M ( x ) = 110101100110, а шаблон ошибки

E ( x ) = 000000001001.

Таким образом, 1 в битовой позиции указывает на ошибку. С применением булевой функции «сумма по модулю 2» полученный кадр - M ( x ) + E ( x ) :

M ( x ) + E ( x )_ M ( x ) E ( x ) G (x)    " G (x) G (x) '

Поскольку M ( x )/ G ( x ) не дает остатка, то ошибка присутствует, если E ( x )/ G ( x ) дает остаток.

Сравнение моделей вероятного кода числа PNC и циклического избыточного кода CRC

Например, G ( x ) имеет по крайней мере три не нулевых слагаемых (1 бит), и E ( x )/ G ( x ) будет давать остаток для всех однобитовых и всех двубитовых ошибок с арифметикой по модулю 2, следовательно, ошибки обнаруживаются. И наоборот, ошибка длиной G ( x ) не дает остатка и остается незамеченной [12].

Генераторный многочлен из R бит обнаруживает [13]:

– все однобитовые ошибки;

– все двухбитные ошибки;

– все нечетные числа бит-ошибок;

• -    все пакеты ошибок ^ R ;

• -    большинство пакетов ошибок >  R .

Пример вычисления остатка для построения CRC кодового слова и оценки вычислительной сложности

Вычисление CRC детально показано на Рисунке 4, где информационный кадр – 1101011011

генераторный полином – 10011

кадр с дополнительными нулями – 11010110110000

1100001010 частное

10011 111010110110000

00101 „

01011 V

00000 *

Dioic 4

10100 '

1110 остаток (CRC)

Рисунок 4. Вычисление CRC (CRC кодовое слово (передаваемый кадр) – 11010110111110 [13–15])

Таким образам, пример показывает, что при генераторном полиноме CRC-4-TU (10011) и битовой длине информационного кадра, равной 10 бит, требуется 10 делений и 50 сложений по модулю 2. В общем случае неочевидна зависимость между вычислительной сложностью (число сложений и делений), размером порождающего полинома и размером информационного полинома [16–18].

Сравнение вычислительной сложности моделей PNC и CRC

Расчет числа вычислений, являющегося одной из важных характеристик алгоритма модели PNC в модели PNC, выполняется по следующей формуле:

T pnc = s = X ,                                     (1)

где T_PNC – число тактов операций для вычисления остатка PNC; S – разрядность полинома PNC; X – разрядность полинома, определяющего ПГПСЧ.

Таким образом, число тактов операций зависит от числа использования ПГПСЧ и от разрядности PNC.

R pnc = ( P ■ X ) ,                                        (2)

где R_PNC – число вычислений по операции &; P – размер информационного кадра.

Рассмотрим пример оценки вычислительной сложности с полиномом PNC разрядности 8 и информационным кадром размера 48 по формуле (2): R PNC = (48 • 8) = 384 двоичных операций.

Результаты оценки вычислительной сложности алгоритма формирования PNC, выраженные в числе операций, показаны на гистограмме (Рисунок 5).

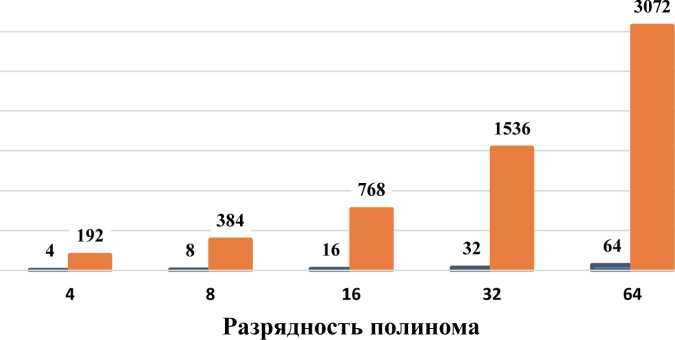
Рисунок 5. Числа операций при формировании PNC для 48-битовых данных

Количество двоичных операций для модели CRC можно определит по формуле

R CRC = N • ( P + N ) mod2 ,                             (3)

где R_CRC – число вычисления по модулю 2; P – размер информационного кадра; N – степень полинома CRC.

Рассмотрим пример оценки вычислительной сложности с полиномом CRC степени 8 и информационным кадром размера 48 по формуле (3): R_crc = (48 + 8) ^ 8 = 448 двоичных операций.

Сравнение моделей вероятного кода числа PNC и циклического избыточного кода CRC

Расчет T_CRC – числа тактов операций для вычисления остатка CRC определяется следующим образом:

T CRC = ^{R CRC} .                                     (4)

N

Результаты оценки вычислительной сложности алгоритма формирования CRC, выраженной в числе операций, показаны на гистограмме (Рисунок 6).

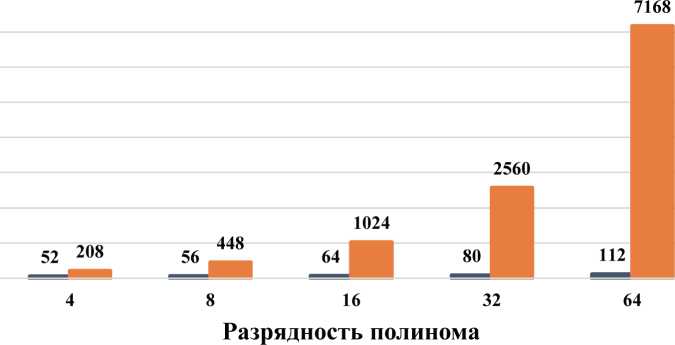
□ Тактовые операции Вычисления мод2

Рисунок 6. Числа операций при формировании CRC для 48-битовых данных

Результаты сравнительного анализа количества тактов (см. формулы (1), (4)), требуемых для вычисления контрольных сумм в моделях PNC и CRC, приведены на Рисунке 7.

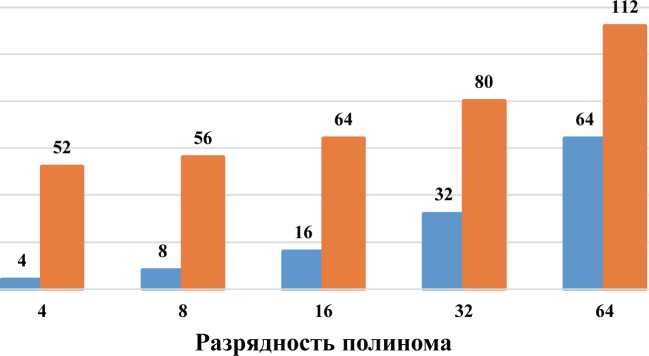
Тактовые операции PNC Тактовые операции CRC

Рисунок 7. Число тактовых операцийв зависимости от разрядности полинома

Таким образом, результаты анализа показали, что по числу тактовых операций модель формирования PNC более эффективна, чем модель CRC.

Сравнение модели PNC и CRC по обнаружению ошибки

Коды PNC и CRC обладают высокой достоверностью обнаружения искажений. Вероятность P ₀ обнаруживаемых искажений не зависит от длины защищаемого информационного данных, а определяется только степенью N порождающего полинома [19]:

P o = 1 - 2 ^- N •

Таким образом, для PNC4 и CRC4 P0 = 1 - 2-4 = 0.9375. Исходя из того, что разрядность контрольной суммы PNC4 и CRC4 составляет 4 бита, очень высока вероятность возникновения коллизий, поскольку максимально допустимое число комбинаций кон- трольной суммы PNC4 и CRC4 = 24 = 16 [20].

Для оценки вероятности необнаружения искаженных битов и выявления факта коллизий была определена формула для оценки требуемого количества экспериментов по передачи пакетов через канал при фиксированном количестве ошибок в канале. Расчет для сравнения PNC и CRC при n -битовом пакете и при k ошибках реализуется как число сочетаний из n по k :

Ск = n !

n    к !( n - к )!

.

Таким образом, с помощью имитационного моделирования передачи пакетов через канал при фиксированном количестве ошибок в канале получены оценки вероятности не- обнаружения искажений Рне о6 в пакетах:

Y

^Рнеоб      к ,                                             ⁽⁶⁾

Cn где Y – количество пакетов с не обнаруженными искажений.

Результаты расчетов, полученные с помощью формулы (6), приведены на Рисунке 8.

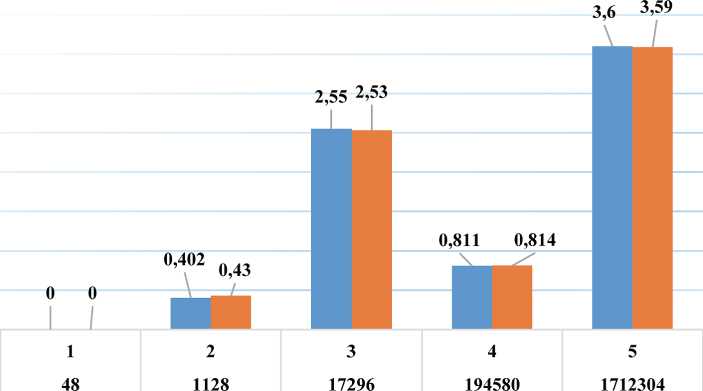
■ Р не o6_PNC ■ Р не o6_CRC

Рисунок 8. Сравнение результатов оценки значении Р _{не о6} , представленных в логарифмическом масштабе, для модели PNC и CRC на необнаруженных ошибочных пакетах

В качестве примера рассмотрим следующую задачу, составленную на основании Рисунка 8. Расчет выполнен с помощью формулы (5):

Сравнение моделей вероятного кода числа PNC и циклического избыточного кода CRC

48 ■ 47 ------= 1128.

2!

В целях упрощения действий приведем ее к следующему виду в соответствии с формулой (6):

----= 0,402.

На Рисунке 8 видно, что модель PNC по сравнению с традиционной моделью CRC обеспечивает меньше вероятности необнаружения искажений, когда количество ошибок оказывается нечетным. Следует отметить, что при четных ошибочных битах модель CRC оказывается лучше.

Заключение

В статье приведено сравнение модели PNC с традиционной моделью CRC. Показано, что у CRC увеличение размера пакета данных при фиксированном размере порождающего полинома увеличивает число тактов.

В статье также показано, что количество таков, требуемых для вычисления контрольной суммы пакета данных в модели PNC, не зависит от размера пакета при фиксированном размере порождающего полинома.

Характеристика обнаружения ошибки не снижается в PNC в отличие от CRC, когда количество ошибок пакетов нечетное. Анализ сравнения позволяет сказать, что PNC не на много уступает при четном количестве ошибок, но показывает лучшие результаты, чем CRC, при нечетном количестве ошибок. Результаты анализа открывают путь для дальнейшего исследования по снижению вычислительной сложности операции расчета контрольных сумм.