Сравнение некоторых методов решения систем линейных уравнений на вычислительных комплексах с гибридной архитектурой на примере задачи вытеснения нефти

«Московский физико-технический институт (национальный исследовательский университет)», 2020

необходимо решать систему линейных алгебраических уравнений. Таким образом, быстродействие используемых численных методов существенно определяется скоростью решения линейных систем. Решение трехмерных задач даже на сравнительно грубых пространственных сетках требует значительных вычислительных ресурсов, из-за чего такие задачи решаются на вычислительных комплексах, состоящих из множества узлов. Для этого расчетная область разделяется на подобласти между всеми процессами, при этом каждый процесс хранит лишь переменные, которые относятся к его подобласти. При необходимости, посредством библиотеки передачи сообщений МРІ, процессы обмениваются между собой значениями переменных, которые прилегают к границе с соседними подобластями. Ниже эффективность методов решения систем линейных уравнений на вычислительных комплексах с гибридной архитектурой изучается на основе симулятора многофазных течений [1], разработанного в лаборатории флюидодинамики и сейсмоакустики МФТИ. При моделировании типичных двумерных задач в однопроцессорном режиме на решение линейных систем указанный симулятор затрачивает до 50% общего времени расчета. При переходе к трехмерным постановкам доля затрачиваемого времени еще более возрастает.

Графические ускорители являются перспективным направлением развития суперкомпьютерной вычислительной техники. Этому способствует их высокая производительность (один графический ускоритель способен производить до 5 • 1012 операций с плавающей точкой в двойной точности в секунду) и высокая скорость обмена данными с памятью ускорителя (порядка 400 Гб/с). В то же время, графический ускоритель является существенно векторным устройством, то есть для эффективного использования его потенциала алгоритмы должны производить операции над большим объемом данных за одну инструкцию. Другой сложностью является тот факт, что ускоритель фактически является внешним устройством. Любые обмены между графическим ускорителем и центральным процессором, а также между двумя графическими ускорителями, расположенными на различных узлах, производятся через шину данных, обладающую существенно меньшей пропускной способностью (до б Гб/с).

В данной работе изучается вопрос целесообразности применения графических ускорителей на базе архитектуры CUBA [2] для уменьшения времени, затрачиваемого на решение линейных систем в характерной задаче моделирования многофазной фильтрации.

• 2.    Рассматриваемые системы линейных уравнений

• 2.1.    Численный метод решения системы

Будем рассматривать системы линейных уравнений, которые возникают при дискретизации уравнений в частных производных эллиптического или параболического типа на прямоугольных равномерных расчетных сетках. Пространственные операторы будем аппроксимировать на минимальном семиточечном шаблоне типа «крест» (изображен на рис. 1). Далее предполагаем, что под индексами i,j,k имеются в виду номера ячеек по трем осям декартовой системы координат.

Дискретизированное уравнение относительно неизвестной сеточной функции и в узле (i, j, k) имеет вид x-j,k Ui-1,j,k + У-k Uij-1k + Z-,k Ui,j,k-1 + ci,j,k п^к +

+ Z+,j,k Ui,j,k+1 + y+j,k Ui,j+1,k + xt,j,k Ui+1,j,k = fi,j,k, где x-,y-,z-,c,x+,y+,z+ — известные коэффициенты дискретизации. / — известная правая часть. В матричном виде система записывается как Au = f. Строго нижнюю часть матрицы A обозначим как A-. а строго Bej:>хиюю — как A+. Несложно видеть, что A-будет содержать лишь значения коэффициентов с индексом « —», a A+, наоборот, с индексом «+». Диагональную часть матрицы A обозначим как C, она будет состоять лишь из коэффициентов Ci,j,k- Таким образом, A = A- + C + A+.

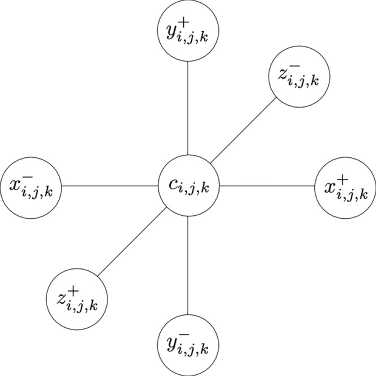
Рис. 1. Трехмерный пространственный шаблон разностной дискретизации

Матрица системы A относится к классу разреженных. В настоящей работе система с данной матрицей решается итерационным методом BiCGStab с правым предобуславлива-нием [3] (алг. 1). Хорошее предобуславливание является ключевым фактором при решении больших разреженных систем, полученных при дискретизации эллиптических операторов, поскольку такие системы характеризуются большим числом обусловленности, которое растет при измельчении разностной сетки. Выбор хорошего предобуславливателя является компромиссом между скоростью решения вспомогательных систем и уменьшением количества итераций метода. Так как решение вспомогательной задачи с предобуславливателем выполняется на каждой итерации метода, для снижения количества обменов между процессами используется локальное предобуславливание. При этом матрица предобуславливателя является блочно-диагональной. Каждый блок матрицы соответствует одной подобласти

А =	/ А11 А 21 • •	А12 . А 22  . •                  • •	..  А1р\ ..   А2р • •                      •	, м =	/М11 М 22 •	⎟
	• \А р1	• А р2  .	•                • .. Арр/		1	м J

,   М_гг = ILUo (А _гг ) .

Все векторы в алгоритме хранятся в распределенном по процессам виде, при этом векторы ж, / дополнительно хранят копию значений в приграничных узлах соседних подобластей. Синхронизация этих значений происходит непосредственно перед выполнением операции MATVEC. Межпроцессное взаимодействие также происходит в операциях вычисления скалярного произведения DotProduct (u, v) и нормы вектора ||w||, но в этом случае требуется лишь просуммировать значения, полученные при вычислении частичного скалярного произведения независимо для каждой подобласти. Остальные операции, включающие PrecondSolve и линейные операции с векторами, не требуют взаимодействия между процессами.

• 2.2.    Неполное LU-разложение

Для данной задачи были протестированы различные предобуславливатели семейства ILU( к). При увеличении параметра к количество итераций алгоритма, необходимых для достижения сходимости, снижалось недостаточно быстро, чтобы скомпенсировать увеличивающуюся вычислительную сложность операции предобуславливания, вызванную увеличением степени заполнения треугольных факторов матрицы. Поэтому, как наиболее удачный по соотношению «эффективность / стоимость», был выбран предобуславливатель ILU(O).

Известно [4], что если матрица имеет структуру ненулевых элементов, полученную дискретизацией на шаблоне «крест», то для ее 1Ы1(0)-разложения справедливо представление

A

M — ( D + A ^-) D ^-1( D + A ⁺), ⏟⏞⏟ ⏞

LU где матрица D состоит из диагональных элементов di,j,k, получаемых из рекуррентного соотношения di,j,k — Ci,j,k

^x i,j,k ^x i - 1,j,k ^d i - 1,j,k

—

^У і jk ^y i,j - 1,k

^d i,j - 1,k

^z i,j,k ^z i,j,k - 1 ^d i,j,k - 1

Это свойство позволяет бвістро и экономно вычислять неполное разложение рассматриваемых матриц.

• 2.3.    Решение систем с треугольными матрицами

Факторизованная структура матрицы M — LU позволяет сводить решение вспомогательных систем Mv — g к последовательности задач с треугольными матрицами

( D + A ) w — g , ( D + A ⁺) v — Dw .

Рассмотрим задачи (1) и (2) подробнее. В индексной форме их можно представить как набор уравнений xi,j,k wi-1,j,k + di,j,k wi,j-1,k + zi,j,kwi,j,k-1 + di,j,kWi,j,k — 9i,j,k, di,j,k vi,j,k + z+j,k vi,j,k+1 + y+j,k Vi,j+1,k + x+j,k Vi+1,j,k — di,j,kWi,j,k.

Предполагается, что для всех i,j,k коэффициенты, лежащие вне расчетной подобласти, равны нулю. Решение таких систем может быть записано в виде рекуррентных соотношений

^ i,j,k ^— л--- ^d i,j,k

(9 i,j,k ~ х-^^ i - 1,j,k ^- y- j,k ^w i,j - 1,k ^{- z-} j,k ^w i,j,k - 1

^X ijA ^— W i,j,k ^- ---- ^d i,j,k

(^x tj,k ^{Vi+1,j,k +} y +j,k^d* ¹ * ^{+ z}i⁺j,k'^Wi,j,k+1) .

Сложность параллельного решения систем уравнений с треугольными матрицами состоит в зависимости по данным в этих рекуррентных формулах. Несмотря на это указанная задача все же обладает потенциалом распараллеливания. Введем так называемый ярус параллельной формы [5] — совокупность неизвестных между которыми нет зависимости. Такими ярусами будут множества {(i,j, k) : i + j + k — const}. Вели чину a = i + j + k будем называть номером яруса. Заметим, что при решении подсистемы с нижнетреугольной матрицей неизвестные величины с яруса а выражаются через неизвестные величины с яруса а — 1, а при решении подсистемы с верхнетреугольной матрицей — наоборот, через неизвестные величины с яруса а + 1.

• 2.4.    Формат хранения данных

Эффективная параллельная реализация алгоритмов решения систем с треугольными матрицами требует, чтобы неизвестные, которые находящиеся на одном ярусе, располагались в последовательных ячейках памяти. В этом случае удается максимально эффективно использовать пропускную способность шины памяти.

Введем индекс 3; который позволяет отличать переменные в рамках одного параллельного яруса. В данной работе был выбран вариант 3 — jNk + k. С использованием этих индексов формулы решения треугольных систем принимают вид

™ а,3 =

"Г1- (Ра,3

^ a,3 ^V

^{— Х-} р W < -1 ,3 ^- y

^ < -1 ,3 __Nk

— ^Z- , ₃ ^W a -1,3-1

X aP = W_a p

-

1— Др « а +1 ,р + У+ р V_a+i ,p ₊ N _k + Щ U_a+i p +1) . ^<,3 +                                                    ⁷

Шаблоны, соответствующие формулам (3), (4), изображены на рис. 2.

Рис. 2. Шаблоны схем решения нижне- и верхнетреугольной системы в а-р индексах

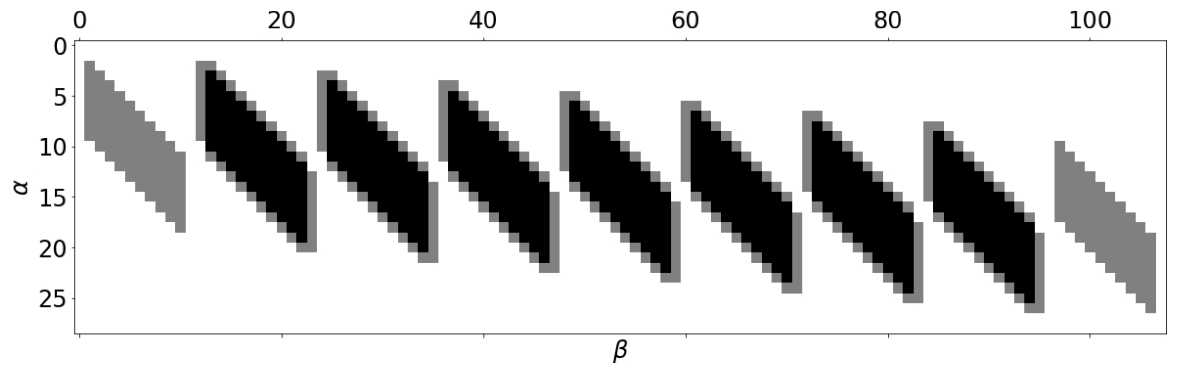
Хранение прямоугольных блоков в а — Р нумерации занимает больше памяти. На рис. 3 представлен блок из 8 х 7 х 10 ячеек в виде двумерного массива в координатах а — р. Белым изображены неиспользуемые элементы, серым — граничные элементы из соседних подобластей, черным — элементы из самой подобласти. Такая схема хранения является довольно избыточной — почти 2/3 элементов никак не используются. Однако она обеспечивает требуемое свойство локальности — ярус параллельной формы целиком располагается в одной строке этого массива. Для краткости будем называть этот способ хранения данных ярусным форматом.

Рис. 3. Прямоугольный блок в ярусном формате. Белым цветом отмечены неиспользуемые ячейки, черным — ячейки, лежащие внутри блока, серым — ячейки, принадлежащие соседним блокам

как на скорости б Гб/с (характерная скорость обмена данными между хост-системой и графическим ускорителем) это займет по 8 нс на один передаваемый элемент. Это время учитывает передачу данных с ускорителя на хост и обратно. Данное время составляет величину порядка времени выполнения операции PRECONDSOLVE на центральном процессоре, что лишает целесообразности использование графического ускорителя в таком сценарии. Таким образом, выделение границ необходимо выполнять на самом графическом ускорителе, передавая минимально необходимый объем данных через память хост-системы и межпроцессную сеть.

Таблица!

Распределение времени работы алгоритма решения линейных систем по отдельным операциям

операция	ВЫЗОВОВ	общее время	время вызова	доля
1Ги(0)-факторизация	864	324 мс	375 мкс	0,58%
синхронизация векторов ж, у	35268	1,37 с	38,9 мкс	2,46%
Matvec	34404	14,2 с	412 мкс	25,5%
PrecondSolve	33540	26,0 с	775 мкс	46,6%
вычисление нормы вектора	18498	1,08 с	58,5 мкс	1,94%
DotProduct	67080	4,44 с	66,2 мкс	7,97%
масштабирование вектора	16770	759 мс	45,3 мкс	1,36%
операция у = у + аж	98892	7,31 с	73,9 мкс	13,12%
Другие		271 мс		0.47%

• 3.1.    Реализация отдельных операций на графическом ускорителе

Операции линейной алгебры (скалярное произведение, взятие нормы, масштабирование и линейная комбинация) реализованы посредством функций из библиотеки cuBLAS [6]. При этом функции библиотеки интерпретируют данные в косом формате как обыкновенный массив. Для корректной работы этих функций достаточно заполнить нулями неиспользуемые элементы ярусного представления. Несмотря на трехкратную избыточность этого представления, скорость работы библиотечных функций позволяет перекрыть накладные расходы на сложность работы с данными в косом представлении.

Операции извлечения и внедрения границ подобластей, необходимые для эффективного обмена данными между процессами, реализованы в варианте без оптимизации шаблона доступа к памяти, каждый элемент выгружается отдельной нитью на графическом ускорителе. Неэффективность реализации компенсируется сравнительно небольшим объемом выгружаемых данных. С ростом линейного размера подобласти доля времени, приходящаяся на выгрузку граничных элементов, будет только уменьшаться, так как на O(N 3) элементов подобласти приходится лишь O(N ²) граничных элементов. Здесь под N понимается характерное количество ячеек вдоль одного пространственного измерения подобласти.

Реализация операции Matvec достаточно прямолинейна. Каждый элемент произведения вычисляется одной нитью на графическом ускорителе. При этом нити с последовательными номерами обращаются к последовательным элементам массивов с данными. Это условие гарантирует эффективное использование пропускной способности шины памяти на видеокарте. Быстродействие данной операции определяется скоростью доступа к памяти и при скорости 500 Гб/с составляет порядка 0.14 нс/элемент. Здесь учтено, что для вычисления одного элемента результата требуется прочитать 7 коэффициентов и один элемент сомножителя.

Наибольший интерес и сложность представляет реализация алгоритмов решения систем уравнений с треугольными матрицами на графическом ускорителе. В отличие от остальных операций, которые могли быть произведены множеством нитей независимо, эта one- рация требует синхронизации между вычислениями каждого яруса параллельной формы. Синхронизация нитей на графическом ускорителе возможна одним из следующих способов:

• 1)    Синхронизация нитей в блоке, которая выполняется на одном физическом мультипроцессоре видеокарты.

• 2)    Неявная барьерная синхронизация между запусками двух последовательных ядер на видеокарте.

• 3)    Глобальная синхронизация нитей, не требующая остановки ядра.

• 4.    Результаты4.1.    Модельная задача

Указанные подходы имеют как преимущества, так и недостатки. Первый вариант является достаточно дешевой операцией, но ограничивает исполнение алгоритма лишь одним мультипроцессором видеокарты, что сокращает ее быстродействие примерно в 20-30 раз (в зависимости от количества мультипроцессоров в видеокарте). Второй вариант требует запуска большого количества очень простых ядер, каждое из которых вычисляет один параллельный ярус. Такое разбиение может быть слишком мелким и накладные расходы на запуск большого числа ядер могут быть значительными. Последняя возможность появилась начиная с версии CUDA 6.1 (архитектура Pascal) и работает с так называемыми коллективными ядрами. Этот вариант выглядит многообещающим, так как лишен недостатков первых двух. Каждый из этих трех вариантов был реализован.

В качестве типичной использовалась задача вытеснения нефти водой в рамках модели Баклея-Леверетта: обе фазы несжимаемы, пористость постоянна. Рассматривается двухфазная фильтрация в пласте прямоугольной формы с непроницаемыми стенками. Фильтрационное течение описывается системой уравнений рЦ- Ч^V = ^-

<9(1 ^{- s)}       / ^^Ko(s)    \

■         — dr, (К     Vp) = Д.

Здесь <р — пористость, К — абсолютная проницаемость, s — водонасыщенность, k _w ,k_o — относительные фазовые проницаемости, p_w,д_о — вязкости в оды и нефти, р — давление, /_w, /_о^— источниковые члены. В роли источников выступают нагнетающая и добывающая скважины, расположенные в разных концах области. Относительные проницаемости были приняты в виде K_w(s) = s², k_o(s) = (1 — s)², вязкости фаз д _ш = 1 мПа • с, р_о = 10 мПа • с, пористость р = 0.1, абсолютная проницаемость К = 1 Дарси, источники/стоки интерпретировались как писмановские скважины с постоянными давлениями 200 и 100 бар соответственно.

Временная аппроксимация уравнений производится неявно по давлению и явно по насыщенности. Аппроксимация конвективных слагаемых производится по противопоточной схеме, причем направление потока определяется противоположно направлению градиента давления. На каждом временном шаге решается эллиптическая задача относительно давления на неизвестном слое по времени р

• —div (к [- + ^) ] Vp^ = /w + /о. V L ^w      До J /

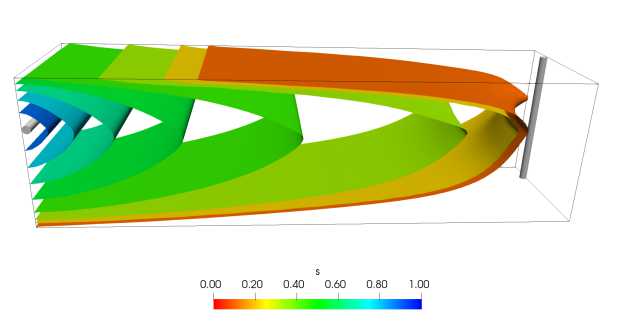
• 4.2.    Сравнение реализаций

Из решения этого уравнения производится перенос поля насыщенности по явной схеме. На рис. 4 приведена картина течения в момент, когда фронт вытеснения достигает добывающей скважины.

Рис. 4. Картина течения в модельной задаче. Цветные изоповерхности являются изолиниями насыщенности, серыми цилиндрами изображены нагнетающая и добывающая скважины

Эксперименты проводились на рабочей станции с графическим ускорителем NVIDIA Titan Хр, имеющим 30 128-ядерных мультипроцессоров. Пиковая пропускная способность памяти видеокарты заявлена в 548 Гб/с. Заявленная пиковая производительность видеокарты на вычислениях с одинарной точностью составляет 12,15 ТФ, а с двойной точностью — 380 ГФ. Несмотря на существенное отличие производительности указанного ускорителя на вычислениях с одинарной и двойной точностью (ровно в 32 раза), для рассматриваемой задачи это оказывается несущественным. Все рассматриваемые операции, реализованные на видеокарте, относятся к классу ограниченных быстродействием памяти. Действительно, во всех этих операциях на один обрабатываемый элемент приходится всего лишь несколько (менее 5) операций с плавающей точкой. Несложно видеть, что при скорости выгрузки данных в 68,5 • 109 элементов в секунду, вычислительные ядра будут успевать обрабатывать данные быстрее.

Итерационный алгоритм решения линейной системы был реализован в нескольких вариантах — в виде программы для центрального процессора, а также в виде трех различных программ, использующих графический ускоритель. Отличие этих программ заключалось в способе реализации операции PrecondSolve. В варианте vl использовался только один мультипроцессор видеокарты, а синхронизация нитей производится в пределах одного блока нитей. В варианте v2 последовательно запускается множество ядер, каждое из которых вычисляет результат на одном параллельном ярусе. В варианте v3 используется глобальная синхронизация нитей в ядре, доступная в последних версиях архитектуры CUDA.

Сравнение производилось на задачах различного размера — на сетках от 40 х 22 х 22 до 200 х 110 х 110 ячеек. Сравнение производилось с использованием одного процесса, но с имитацией межпроцессного обмена. В табл. 2 и табл. 3 приведено сравнение общего времени, занимаемого каждым этапом решения линейной системы. Под Sync понимаются операции межпроцессного обмена, а в случае графического ускорителя — еще и затраты на обмены между ним и центральным процессором. Под BLAS-1 подразумеваются все операции линейной алгебры с векторами (вычисление норм и скалярных произведений, линейная комбинация и масштабирование).

Можно заключить, что оптимальная реализация операции PrecondSolve на графическом ускорителе — это v2. Она быстрее остальных на всех сетках, кроме самой грубой. Как в версии для центрального процессора, так и в версии для графического ускорителя, более половины времени решения линейной системы занимает операция PrecondSolve.

При увеличении размера задачи растет и ускорение А, которое определяется как отношение общего времени работы варианта для центрального процессора к общему времени работы варианта для графического ускорителя. Максимальное ускорение в 12 раз было достигнуто на самой подробной сетке. Можно предположить, что дальнейшее увеличение размера сетки приведет к еще большему ускорению. Однако на практике количество ячеек, приходящееся на одну подобласть, редко выбирают большим 106. Результаты также показывают, что использование графического ускорителя для небольших задач (с количеством ячеек на подобласть менее 105) бессмысленно, так как накладные расходы на синхронизацию между графическим ускорителем и центральным процессором перекрывают время решения задачи на центральном процессоре.

Т а б л и ц а 2

Сравнение времен в мс, затраченных на каждый этап решения задачи на разных расчетных сетках. Вариант для центрального процессора

Сетка	Sync	BLAS-1	Matvec	PrecondSolve
40 х 22 х 22	4,74	69,14	50,5	154,5
80 х 44 х 44	39,6	1320	1160	2990
120 х 66 х 66	180	6900	6000	15480
160 х 88 х 88	384	21030	17580	45630
200 х 110 х 110	1180	49960	43340	107100

Т а б л и ц а 3

Сравнение времен в мс, затраченных на каждый этап решения задачи на разных расчетных сетках. Вариант для графического ускорителя

Сетка	Sync	BLAS-1	Matvec	PrecondSolve			Ускорение
				vl	v2	v3
40 х 22 х 22	37	78	10	267	350	557	0,71x
80 х 44 х 44	127	305	75	1880	1290	2090	3,06x
120 х 66 х 66	240	1090	307	7580	2900	4180	6,30x
160 х 88 х 88	371	2610	846	18400	5360	7050	9,21x
200 х 110 х 110	615	5350	1850	38020	8890	11000	12,06x

• 5.    Заключение

В настоящем исследовании изучен вопрос о целесообразности применения графических ускорителей для решения систем линейных алгебраических уравнений, полученных дискретизацией эллиптических задач на прямоугольных сетках. Существенного ускорения удается добиться на задачах, в которых в подобласти имеется хотя бы 105 ячеек. При этом значения ускорения не могут быть слишком высокими, так как определяются не вычислительной мощностью графического ускорителя, а пропускной способностью шины памяти и накладными расходами на внутреннюю синхронизацию. Данная картина достаточно типична для задач, которые не являются вычислительно-трудоемкими.

В этих условиях требуется обеспечить максимально эффективное использование шины памяти графического ускорителя. Показано, как этого можно добиться, переупорядочив неизвестные «косым» образом.

Авторы благодарят И. В. Цыбулина, без консультаций которого эта работа была бы невозможна.

Работа выполнена при финансовой поддержке РФФИ, грант 16-29-15123.