Сравнение непараметрических критериев проверки гипотез о распределениях случайных величин

Для проверки гипотез о распределениях случайных величин широко используется критерий согласия Пирсона, который не зависит от распределений случайных величин и их размерности [1]. Однако методика формирования критерия Пирсона содержит трудно формализуемый этап разбиения области возможных значений случайной величины на многомерные интервалы. Данный этап отсутствует в критерии Смирнова [2] и методике, основанной на использовании непараметрических алгоритмов распознавания образов [3; 4].

Проведем сравнение эффективности указанных критериев при проверке гипотезы о тождественности законов распределения одномерных случайных величин по данным вычислительных экспериментов.

Традиционные непараметрические критерии. Пусть X ₁ и X ₂ – две генеральные совокупности с произвольными законами распределения.

Необходимо по независимым выборкам V 1 = ( x i , i = 1, n 1 ) и V 2 = ( x i , i = 1, n ₂ ) , извлеченным из данных генеральных совокупностей, проверить либо опровергнуть гипотезу

H . : P ( X 1> P ( X 2 )

о тождественности законов распределения.

Методика проверки статистической гипотезы H _о на основе критерия Смирнова сводится к выполнению следующих шагов.

Шаг 1. По независимым выборкам V ₁ , V ₂ построить оценки функций распределения

1 n_j

Pj(.x)      Z'lx-xi), j =1,2, nj i=1

где

< i\ 10, еслиx-xi <0, 1( x - xi ) = < v 7 11, если x - xi > 0.

Шаг 2. Найти максимальное расхождение между эмпирическими функциями распределения

D 12 = max | P ( x ) ^- P 2 ( x )| .

x

Шаг 3. В соответствии с критерием Смирнова [5] сравнить полученное максимальное расхождение D ₁₂

с пороговым:

al 1      1 I

D„ = - ln— — + — /2 , a

V      ² I ⁿ 1 ⁿ 2 )

где a - принятый уровень доверия, т. е. риск отвергнуть гипотезу H _о .

Если выполняется условие D ₁₂ <  D _a , то гипотеза H „ справедлива, иначе эмпирические законы распределения различаются.

Критерий Пирсона предполагает выполнение следующих шагов.

Шаг 1. Разбить область изменения исследуемых случайных величин на N непересекающихся интервалов. Их количество может быть определено по эвристическим формулам Старджесса

N = log₂ n + 1,

Брукса и Каррузера

N = 5 lg n или Гаеде

N = V n , где n = n 1 + n ₂.

Шаг 2. Вычислить частоты P ₁ ^j , P ₂ ^j , P ₁₂ ^j попадания элементов последовательностей V 1 , V ₂ и V 1 ^ V ₂ в каждый j -й интервал, j = 1, N . Если для некоторого j -го интервала значение P 1 ₂ = 0, то количество интервалов уменьшается на единицу и производится перерасчет размера интервалов и соответствующих им частот. Эта процедура повторяется до тех пор, пока не будет определено количество интервалов N <  N , для которых выполняются условия P 12 * 0, j = 1, N .

Шаг 3. Рассчитать значение случайной величины по формуле [1, с. 330]

( j p4

2 N

Z = Z n t Z t =1 j =1

которое имеет % ²-распределение с к = N - 1 степенями свободы.

Шаг 4. По таблице % ² -распределения определить порог X ( к , а ) одностороннего критерия Пирсона при заданных значениях к и уровне значимости а .

Гипотеза H „ справедлива, если Z < % ² ( к , а ) , иначе она отвергается.

Методика 1 проверки гипотезы о распределениях. Будем полагать, что элементы последовательностей случайных величин V ₁ и V ₂ принадлежат соответственно классам Q ₁ и Q 2 . Сформируем обучающую выборку V = ( x , g ( i ) , i = 1, n ) для решения задачи распознавания образов, где n = n₁ + n ₂; g ( i ) -указание о принадлежности значения xⁱ к тому либо иному классу. На этой основе построим непараметрический алгоритм распознавания образов, соответствующий критерию максимального правдоподобия [6]:

m ( x ) :

x e Q1, x eQ2,

если f i2 ( x ) < 0, если f_; 2 ( x ) > 0.

При формировании оценки уравнения разделяющей поверхности

f12 ( x ) = P2 ( x )- P1 ( x )              (2)

можно использовать непараметрические оценки p ₁ ( x ) , p ₂ ( x ) плотностей вероятности распределения x в классах Q ₁, Q 2 типа Розенблатта-Парзена [7]. Тогда статистика (2) будет представлена выражением

( - I f2 (x) = (nc) ZCT1 (i) Ф|------ I, i=1

где

J- P — ¹ V x i eQ i ,

°i (1 M,

[ P ₂ ^{- 1} V x i eQ ₂;

nj

Pj = — - оценка априорной вероятности принадлеж-n ности ситуаций обучающей выборки к классу Q j, j = 1,2. Ядерные функции в статистике (3) удовлетворяют условиям Ф(и) = Ф(-и), 0 <Ф(и) <да, +х j Ф(и)du = 1, а значения их коэффициентов размыто--да сти c убывают с ростом количества элементов множеств Vj, j = 1,2.

Выбор оптимального значения c коэффициента размытости непараметрического решающего правила m ( x ) осуществляется по условию минимума оценки вероятности ошибки распознавания образов

n

р( ct), 5( t)), n t=1

где индикаторная функция

, _ Jo V

1(°( t), c( t )) = •! v

°⁽ t ) = с⁽ t ) g ( t ) * 5 ( t ) ;

g ( t ) - решение о принадлежности значений x¹ к классу Q ₁ либо Q ₂ , полученное в соответствии с алгоритмом распознавания образов (1).

При вычислении р(c) решение 5(t) алгоритма (1) определим в соответствии со знаком статистики ~                       n              ( yt — Yi I f2 (xt ) = (nc )-1ZG1 (i ) Ф| ------- I , i=1            v c J i * t т. е. ситуация xt , которая подается на контроль, исключается из процесса обучения.

Известно, что если при решении двуальтернативной задачи распознавания образов вероятность ошибки классификации равна 0,5, то законы распределения случайных величин в области определения классов совпадают. Поэтому появляется возможность перехода от задачи сравнения законов распределения случайных величин к проверке гипотезы Hо о равенстве статистической оценки вероятности ошибки распознавания образов значению 0,5.

Проверим гипотезу H„: р( c) = 0,5 в соответствии с критерием Колмогорова. Для этого сравним его по- роговое значение

D

а

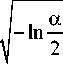
ⁿ 1 ^{+ n} 2

/2

с отклонением D₁₂ = 0,5 -р ( c ) при вероятности а отвергнуть правильную гипотезу H „ .

Гипотеза H _о справедлива при выполнении условия D ₁₂ <  D _а , иначе она отвергается.

Существуют условия, когда использование предлагаемой методики и критерия Смирнова приводит к сопоставимым результатам. К таким условиям относятся задачи проверки гипотез при разных законах распределения случайных величин и одинаковых законах распределения, когда объемы сравниваемых последовательностей V ₁ , V ₂ отличаются незначительно [3].

Для различных объемах случайных последовательностей, например при n1 = 2n2, установлено снижение эффективности методики 1 по сравнению с критерием Смирнова. Данный факт согласуется с результатами работы [8], где показано значительное снижение аппроксимационных свойств непараметрической оценки уравнения разделяющей поверхности при увеличении степени неравномерности распределения элементов обучающей выборки между классами.

Методика 2 проверки гипотезы о распределениях. Пусть количество элементов исследуемых последовательностей случайных величин отличается значительно, например n 1 >  n 2 . Сформируем набор сравниваемых последовательностей ( V ( j ) = ( x , ^{1 е} I j ) , V 2 = ( x i , i = 1, n 2 ) ) , j = 1, T , где I_j – множество номеров элементов последовательности V ₁ , составляющих сравниваемую последовательность V 1 ( j ) . Элементы выборки V 1 ( j ) объемом n ₂ формируются случайным образом из последовательности V ₁ .

В соответствии с методикой 1 проверим гипотезы H о ( j ) : P j ( c ) = 0,5 и по полученным данным рассчитаем оценки вероятностей Р _о = ST , P = S/T справедливости гипотезы H _о и ее отклонения соответственно. Здесь S – количество решений о справедливости, а S - об отклонении гипотез H _о ( j ) , j = i? T .

Проверим достоверность отличия P ¹ и P с использованием критерия Смирнова. Для этого вычислим его пороговое значение

D = - in ^a / t , ^a V 2

которое сравним с разностью D = р _о - P |.

Исходная гипотеза H _о подтверждается, если D >  D _a и Р _о >  P , в противном случае, т. е. при Р _о <  P , она отвергается.

Анализ результатов вычислительных экспериментов. Сравним эффективность приведенных выше методик проверки гипотезы о распределениях случайных величин по данным вычислительных экспе- риментов.

Последовательности случайных наблюдений

V1 =(xi, i = 1, n1) и V2 =(xi, i = 1, n2) формирова- лись на основе датчиков случайных величин с равномерным    xi = е i    и нормальным

( 12        )

xi = 0,5 + 0,15 ^еj -б|, i = 1, n, законами распре деления. Случайные величины е с равномерным законом распределения определены на интервале [0,1].

При их формировании использовался стандартный датчик псевдослучайных величин среды визуального программирования Delphi.

Вычислительные эксперименты при фиксированных условиях исследования проводились 100 раз. По полученным результатам оценивалась вероятность Fo выполнения гипотезы Hо о тождественности законов распределения случайных величин на основе исследуемых методик. Риск а отвергнуть гипотезу Hо принимался равным 0,05.

Синтез непараметрического классификатора осуществлялся на основе параболических ядерных функции В. А. Епанечникова [9]. При формировании методики 2 значение T = 10. В критерии Пирсона использовалась формула Старджесса для разбиения области изменения исследуемых случайных величин на N интервалов.

Были получены следующие зависимости оценок вероятностей Fo выполнения гипотезы Hо от объема экспериментальных данных при априори тождественных (табл. 1, 2) и разных (табл. 3) законах распределения случайных величин. В таблицах использованы следующие обозначения: КС – критерий Смирнова; М1, М2 – методики 1 и 2 соответственно; КП – критерий Пирсона.

Таблица 1

Зависимости оценок вероятностей Fo справедливости гипотезы Ho от объема экспериментальных данных n=n1+n2 при n1=1,2n2 в условиях сравнения двух априори тождественных законов распределения случайных величин

n	Равномерные законы распределения				Нормальные законы распределения
	КС	М1	М2	КП	КС	М1	М2	КП
22	0,97	0,98	0,99	0,98	1,00	0,98	0,98	0,98
66	0,96	0,95	0,96	0,94	0,98	0,96	0,98	0,98
110	0,98	0,95	0,96	0,99	0,99	0,99	1,00	0,97
154	0,96	0,92	0,97	0,96	0,96	0,93	0,97	0,97
198	0,98	0,93	0,96	0,92	0,99	0,97	1,00	0,96
242	0,97	0,96	0,97	0,95	0,96	0,96	0,96	0,91
286	0,96	0,92	0,94	0,98	0,96	0,94	0,95	0,96
330	0,96	0,94	0,95	0,97	0,97	0,94	0,98	0,97
374	1,00	0,93	0,97	0,99	0,96	0,93	0,95	0,95
418	0,97	0,93	0,95	0,98	0,97	0,93	0,96	0,96
462	0,96	0,91	0,94	0,94	0,96	0,9	0,94	0,95

Таблица 2

Зависимости оценок вероятностей Fo справедливости гипотезы Ho от объёма экспериментальных данных n=n1+n2 при n1=2n2 в условиях сравнения двух априори тождественных законов распределения случайных величин

n	Равномерные законы распределения				Нормальные законы распределения
	КС	М1	М2	КП	КС	М1	М2	КП
30	0,99	0,98	1,00	0,98	0,99	0,98	1,00	0,94
90	0,98	0,93	0,99	0,99	0,98	0,92	0,99	0,95
150	0,96	0,86	0,97	0,95	0,97	0,87	0,99	0,98
210	0,98	0,82	0,96	0,96	0,97	0,73	0,99	0,94
270	1,00	0,77	0,99	0,99	0,96	0,69	1,00	0,97
330	0,93	0,70	0,97	0,91	0,98	0,65	0,99	0,97
390	0,94	0,74	0,96	0,96	0,97	0,63	0,97	0,94
450	0,96	0,67	0,97	0,97	0,94	0,61	0,98	0,95

Таблица 3

Зависимости оценок вероятностей Fo справедливости гипотезы Ho от n в условиях сравнения нормального и равномерного законов распределения случайных величин

n = n 1 + n 2 при n 1 = 1,2 n 2					n = n 1 + n 2 при n 1 = 2 n 2
n	КС	М1	М2	КП	n	КС	М1	М2	КП
22	0,84	0,76	0,93	0,65	30	0,9	0,45	0,89	0,53
66	0,58	0,21	0,27	0,22	90	0,53	0	0,10	0,02
110	0,23	0,01	0,03	0,01	150	0,17	0	0,02	0
154	0,14	0	0	0,01	210	0,03	0	0	0
198	0	0	0	0	270	0	0	0	0

Анализ данных табл. 1 показывает, что если сравниваемые законы распределения случайных величин априори тождественны, то эффективность критериев Смирнова и Пирсона и методики 2 достоверно не отличается. Показатели методики 1 сопоставимы с ними при малых объемах обучающей выборки ( n < 100). Однако эффективность это методики существенно

n снижается с ростом отношения — (n1 > n2) и зна-n2

чений n .

При анализе последовательностей случайных величин с равномерным и нормальным законами распределения в условиях n > 200 сравниваемые критерии безошибочно отклоняют гипотезу H0 (см. табл. 2). При n < 30 результаты их использования неудовлетворительны. В интервале 30 < n < 180 применение критерия Смирнова нецелесообразно, так как ему свойственна большая вероятность подтверждения гипотезы Hо в условиях априори разных законов распределения случайных величин. При этом эффективность критерия Пирсона, методик 1 и 2 сопоставима n и повышается с ростом отношения 1 .

n ₂

Таким образом, применение принципов коллективного оценивания позволяет повысить эффективность методики 1 проверки гипотезы о распределениях случайных величин, основанной на непараметрическом алгоритме распознавания образов. Показатели методики 2 и критерия Пирсона сопоставимы.

Их применение по сравнению с критерием Смирнова является более предпочтительным в условиях малого объема анализируемых случайных последовательностей. Преимущество методики 2 состоит в обходе проблемы декомпозиции области значений случайных величин на интервалы, свойственной критерию Пирсона. Перспективность этой методики заключается в возможности ее обобщения на решение задач проверки гипотез о распределения многомерных случайных величин.