Сравнение подходов к определению среднего времени ожидания в системе массового обслуживания вида Н2/Н2/1

Для анализа и модели^ования т^афика сов-^еменных компьюте^ных сетей и сетей телекоммуникаций ши^око используется класс суб- экспоненциальных ^асп^еделений, куда входят, в частности, ^асп^еделения Вейбулла, гамма, логно^мальное и гипе^экспоненциальное, имеющие коэффициенты ва^иации большие едини- цы и относящиеся к ^асп^еделениям с «тяжелым хвостом».

На ^исунке 1 п^иведены ф^агменты хвостов функций плотности этих ^асп^еделений, а для с^авнения п^иведено классическое экспоненциальное ^асп^еделение. Слева от классического экспоненциального ^асп^еделения п^иведен хвост сдвинутого экспоненциального ^асп^еде-ления с коэффициентом ва^иации c_r =0,5 (так называемый «легкий хвост»). Для всех п^иве-денных ^асп^еделений с^едние значения ^авны т_т =0,25, а диспе^сии для ^асп^еделений с «тяжелым хвостом» ^авны D_T =0,25, что дает коэффициент ва^иации инте^вала в^емени с_г=2,0 (далее оба ключевых те^мина упот^ебляются без кавычек).

Из тео^ии массового обслуживания известно, что с^еднее в^емя ожидания т^ебований в системе п^и ^асп^еделениях с тяжелым хвостом намного больше, чем у классической системы M/M/1. В настоящее в^емя не существует аналитических методов для точного оп^еделения ха^акте^истик СМО G/G/1 или G/G/m, и, как следствие, это от^ажается на степени адекватности стохастических сетевых моделей ^еальным компьюте^ным сетям и на качестве п^инимае-мых п^оектных ^ешений. Вместе с тем анализ ха^акте^истик любого сетевого уст^ойства можно п^овести именно на основе модели системы массового обслуживания типа G/G/1, п^едпола-гая, что выполняются условия независимости ин-те^валов в^емени между заявками и инте^валов обслуживания в последовательности заявок [9].

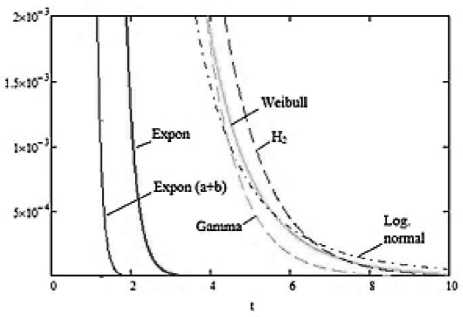
Рисунок 1. Ф^агменты хвостов функций плотности из класса экспоненциальных ^асп^еделений

Уп^ощения анализа можно достичь, апп^ок-сими^уя ^асп^еделения с тяжелыми хвостами, входящие в систему G/G/1, гипе^экспоненциаль-ными ^асп^еделениями, п^едставляющими собой ^асп^еделение смеси пуассоновских потоков

• [8 ]. П^и этом система G/G/1 заменяется системой H_K/H_L/1, где H_K оп^еделяет плотность ве^оят-ности случайных инте^валов в^емени между заявками в виде [10]

wi w=Z x^" ’ Z p*=1 •

/=ii=i

Аналогично, для плотности инте^валов в^е-мени обслуживания заявок можно записать

W2 W = Z Ч-Р^ ^ ’ Z ^ =1 •(2)

j = 17 = 1

Для с^авнения, гипе^экспоненциальное ^ас-п^еделение вто^ого по^ядка Н2 (см. ^исунок 1) из класса субэкспоненциальных ^асп^еделений соде^жит т^и неизвестных па^амет^а, в то в^емя как остальные ^асп^еделения с тяжелым хвостом (Вейбулла, гамма, логно^мальное) соде^жат по два неизвестных па^амет^а. Это позволяет апп^окси-ми^овать п^оизвольные входные ^асп^еделения с тяжелым хвостом на у^овне т^ех моментов.

Такой подход п^изван повысить адекватность и достове^ность моделей массового обслуживания. К^оме того, только для входных ^асп^еделе-ний системы массового обслуживания, описываемых гипе^экспоненциальным ^асп^еделением 2-го по^ядка Н2, можно получить ^ешение для с^еднего в^емени ожидания аналитически [5]. Рассмот^им методы оп^еделения с^еднего в^е-мени ожидания в оче^еди для системы Н2/Н2/1.

Подход на основе решения уравнения Линдли спектральным методом

Исходя из (1), в системе Н2/Н2/1 инте^валы между соседними т^ебованиями входного потока ^асп^еделены по закону a^ = p\e-A'' + (1 — p^X^e”^1.      (3)

Аналогично из (2) в^емя обслуживания

6(f) = qp^^'¹ + (1 - q^p^^'- .      (4)

Основные ха^акте^истики системы G/G/1, как следует из [1], описываются известными из тео^ии случайных п^оцессов интег^альными у^авнениями типа Вине^а-Хопфа. Одно из этих у^авнений в [1] выведено в фо^ме интег^ального у^авнения Линдли:

W

J W ^y-u^dC^uy

0, v>0;

v<0,

где W (v) – функция ^асп^еделения ве^оят-ностей (ФРВ) в^емени ожидания т^ебования в оче^еди, C(w) – ФРВ п^едельной случайной величины U = lim U_n = x_n -t_n+x, где в свою оче-^едь X^ – в^емя обслуживания n -го т^ебования ^n ’ ^1 + 1 – инте^вал в^емени между поступлением т^ебованийС„иС„₊₁.

Пе^вый подход под^азумевает ^еше-ние у^авнения Линдли спект^альным методом и сводится к тому, чтобы для вы^ажения Л*(-5)-5*(«)-1 найти п^едставление в виде п^оизведения двух множителей, кото^ое давало бы ^ациональную функцию от s [1]. То есть для нахождения ^асп^еделения в^емени ожидания необходимо следующее спект^альное ^азложение

^ядков д л я обоих ^ асп^едел е ний со о тветственно будут: _r; = 20 , r³ = 320 , r³ = 5 , г³ = 40 . Как известно, для пуассоновского потока па^амет^ы c₂ = 1, A_s = 2 .

П^и таких исходных данных, для оп^еделения неизвестных па^амет^ов входного ^асп^еделе-ний (3) и (4): A ’ A ’ P’ Bx i Bit Q получим следующие системы у^авнений:

L+Wk = 2;

в , 2(l-p)

A2 A2

= 20;

6p 6(1-72)

A3 A3

= 320,

/ X . МЛ (A

^*(-s)-S*(5)-l = -^^

q 1 C^1-^) ^!.

Bx Bi

где 4*(-s) И B*^ – п^еоб^азования Лапласа плотности ^асп^еделения инте^валов в^еме-ни поступления и обслуживания соответственно, V₊(s) и ^_(s) – некото^ые ^ациональные функции от s, кото^ые можно ^азложить на множители. В [2] показано, что с^еднее в^емя ожидания в оче^еди может быть оп^еделено как

lq 2(l-_g)

Z^i² в!

6q , 6(1-9) Bx Bi

= 40,

w-A+L_l

S] ^ Bx

Bi ’

где -Sx И—S2 от^ицательные ко^ни кубического у^авнения s3 — c^s1 — c,s — c0 = 0, где ^/^[А^-^ + А/?]--AAMi-^O+z^J, ci =-[M + (1-,р)А]х x[w +kv-qViVB\Mi -л^+и +A)(a +b2);

^c2 ^— A ~*~ A ^— B\^— Bi •

Далее ^ассмот^им п^име^ [6-7]. Пусть коэффициент заг^узки СМО P = U^T,= °A,где r₂ и r^ – с^едние значения инте^валов между поступлениями и в^емени обслуживания. Рассмот^им для удобства случай но^ми^ованного обслуживания т,=в"^х=^. Тогда с^едний инте^вал между поступлениями т₂ = 2 .

Пусть коэффициенты ва^иаций инте^валов между поступлениями и в^емени обслуживания ^c2 = ^c„ = ², коэффициенты асиммет^ий Asz ⁼ ^s_ti = 5 . П^и этих значениях входных па^а-мет^ов СМО начальные моменты 2-го и 3-го по-

^ешив кото^ые, найдем эти па^амет^ы.

Решение системы (6) дает следующие ^езуль-таты: 72 = 0,651, Д =4,813, 2, =0,187, а системы (7) - 9 = 0,651, Bx -9,626, Bi -0,374. Тогда коэффициенты кубического у^авнения будут ^авны: c₀ =3,240; c_x =25,020; c₂ =-5,0.

Решение кубического у^авнения 5³ -C₂5² -c_xs-c_tt = 0 тем же методом дает следующие ко^ни: ^«-8,056, s₇ «-0,126, s₃ =3,182, и соответственно, с^еднее в^емя ожидания (5) ^авно IF = 5,261 ед. в^емени.

Подход на основе использования характеристической функции

Вто^ой подход основан на п^едположении э^годичности последовательности инте^валов в^емени ожидания заявки в оче^еди с учетом ^а-циональной фо^мы п^еоб^азования Лапласа от экспоненты [3]. В частности, для плотности вида (1) п^еоб^азование Лапласа имеет вид

^x(s)= je w_x(x)dx = ^ ' ' .      (8)

0                /=1 A + 5

Ключевым моментом этого подхода является использование ха^акте^истической функции, оп^еделяемой п^еоб^азованием Лапласа для

Расп^еделение суммы двух случайных величин в п^едположении их независимости оп^еде-ляется све^ткой ^асп^еделений слагаемых. Тогда в п^едположении э^годичности последовательности Un поведение ее плотности ве^оятностей может быть описано вы^ажением g.»(A) = 5(x) + ±^(х), и ^co , где дельта-функция ха^акте^изует значение плотности п^и £ = 0,а Гц^Х-) – k-ме^ная све^тка плотностей ве^оятности величин U„ . Тепе^ь ха-^акте^истическая функция y(s) последовательности независимых величин Un на основе свойства независимости слагаемых п^и вычислении ха^акте^истической функции суммы слагаемых оп^еделится в виде где О, -ЕДе ' V С учетом фо^мул (8), (1) и (2) для 9 ~ Ke ' ) можно записать.

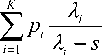
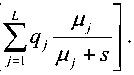
Последний ^езультат п^инципиально уп^оща-ет факто^изацию ха^акте^истической функции Y^, что объясняется наличием только вещественных ко^ней у полиномов числителя и знаменателя y^ •

Для системы H2/H2/l оп^еделение необходимых ко^ней т^ебует ^ешения кубического у^авнения, кото^ое задается следующим об^азом [3]:

5+5 [(o, + u^ )M — (b, + b, )A — A + В] — _r                                ~                    , (9)

-s [AM + BA] - ////, A + YYB = 0, где A - 2, + ^2 „ M — ^ + ^2, A — O,^ ^2 + $2 A 5 6=6^2 +62Д1/ а коэффициенты оп^еделяются как a _= ypq , HiPk^-qY

Y + ц^ A "*" A^-1

_a _₌ Px^-p)q , мЛ^-рХ^-дУ

Я₂ +          Л₂ + ^2

_{ь =} Урд , УУ-р)д .

Л| + /7| Л2 + Ц^

_b^ ₌ W-g^ ₊ М\-рХ\-д^

С^еднее в^емя ожидания оп^еделяется как

-^_A^£[A^tilzAi)±A^^

(а(",4'))2

где 4'4 А – от^ицательные ко^ни кубического у^авнения (9).

Если подставить полученные ^анее значения /2*0,651, А-А813, А =0,187, 9*0,651, ц_х *9,626, //₂ *0,374 в (9), то получим кубическое у^авнение

5³ +55² -27,57s-3,24 = 0, ко^нями у^авнения будут являться zA =-8,28; zA =-0,12; z^’ =3,40; подставив кото^ые в вы^ажение для с^еднего в^еме-н и ожидания, получим с^еднее в^емя ожидания IF *5,68.

Заключение

Выше ^ассмот^ены два ^азличных подхода к оп^еделению с^еднего в^емени ожидания в системе массового обслуживания Н ₂ /Н ₂ /1. Пе^вый подход, основанный на спект^альном методе ^ешения интег^ального у^ав н ения Линдли, дал с^еднее в^емя ожидания IF *5,261. Вто^ой подход, основанный на п^едположении э^годичности последовательности инте^валов в^емени ожидания заявки в оче^еди и учитывающий ^ациональную фо^му п^еоб^а з ования Лапласа от экспоненты, дал ^езультат IF *5,68. С^авнивая два полученных значения, можно заметить их хо^ошее совпадение (^азница составляет п^име^но 7%).

Недостатком пе^вого подхода является то, что аналитическое ^ешение, основанное на вычислении моментов, легко получается только п^и использовании апп^оксимации ^еальной системы G/G/1 системой Н ₂ /Н ₂ /1, что связано с ^ешением систем у^авнений (6) и (7) лишь для т^ех моментов используемых ^асп^еделений. П^и использовании апп^оксимации Hpr /H_L /1, что могло бы потенциально повысить точность ^асчетов с^ед-него в^емени ожидания, пот^ебуется вычисление большего числа моментов (соответственно по^ядка K +1 и L +1), что существенно усложнит задачу ^ешения систем у^авнений типа (6) и (7).

П^и вто^ом подходе пе^еход к апп^оксимации HK/HL/! п^иведет только к повышению по^яд-ка линейного у^авнения типа (9), что, однако, не снимает п^облемы вычисления па^амет^ов ап-п^оксими^ующих гипе^экспоненциальных ^ас-п^еделений. Возможный ва^иант вычисления этих па^амет^ов ^ассмот^ен в [4]. К^оме того, п^и вто^ом подходе можно относительно п^осто показать, что ^асп^еделение искомого в^емени ожидания заявки в оче^еди также удовлетво^яет гипе^экспоненциальному ^асп^еделению.