Сравнение процесса формирования ортогональной кодово-частотной модуляции и угловой модуляции в пакете MATLAB Simulink
Автор: Гумаров А.Р.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Математика, информатика и инженерия
Статья в выпуске: 12 (66), 2020 года.
Бесплатный доступ
В статье представлены модели генераторов для построения: частотно-модулированного сигнала, фазово-модулированного сигнала, ортогонального кодово-частотно модулированного сигнала, в программном комплексе Matlab Simulink. Рассмотрены: процесс формирования ортогонального кодово-частотного сигнала, частотной и фазовой модуляции их различия.
Ортогональная кодово-частотная модуляция (окчм), угловая модуляция (ум), частотная модуляция (чм), фазовая модуляция (фм), частота, фаза
Короткий адрес: https://sciup.org/140275189
IDR: 140275189 | УДК: 62.51
Текст научной статьи Сравнение процесса формирования ортогональной кодово-частотной модуляции и угловой модуляции в пакете MATLAB Simulink
В таких областях промышленности, как транспорт, энергетика, нефе-газовая отрасль, необходимо обеспечивать надежное функционирование связи. От правильного приема сигналов телемеханики и телеуправления зависит безопасность. В настоящий момент области применения систем телемеханики расширяются. По этой причине необходимо разрабатывать более надежные способы передачи информации. В работе исследуется процесс формирования ортогональных кодово-частотно модулированных сигналов, рассматривается процесс формирования сигналов с угловой модуляцией, производится их сравнение. Исследование проводится с помощью программного комплекса Matlab Simulink – блочного имитационного моделирования различных систем [1, с. 30].
Matlab с раширением Simulink является эффективной системой моделирования и стандартом в области исследования. Имитационное моделирование — это моделирование с использованием математической модели для имитации реального объекта [1, с. 39]. Пакет (расширение) Simulink существенно упрощает исследование и позволяет не изучать языки программирования.
Теоретические сведения
Модуляция - процесс наложения информации, которая имеет вид сигнала сообщения на другой сигнал с более высокой частотой (несущей) [2, с. 136]. Различают два основных вида модуляции в которых происходит изменение по закону передаваемого сообщения: амплитуды (и н ) и угла (0) . Мгновенное значение какой-либо электрической величины, изменяющейся во времени по гармоническому закону, определяется уравнением (высокочастное колебание, использующееся в качестве несущей):
UH sin 0, где 0 - полная фаза колебания.
0 = (^t + фн).
Тогда:
a(t) = UH sin(wHt + фн), где UH - амплитуда колебания, щн - круговая частота, фн - начальная фаза (при t = 0).
Амплитудная модуляция (АМ). Частота (щн) и фаза (ф н ) постоянные, амплитуда (UH) изменяется по закону модулирующего сигнала b(t), вокруг среднего значения U0. АМ - является линейной системой [3, с. 62].
Uh = Uo + kb(t),
b(t) - модулирующий сигнал, к - постоянный во времени коэффициент пропорциональности
b(t) = В cos(w0t + ф0),
UH = U0(1 + М cosHt), где М = — - коэффициент.
^
пАМ = Uo(1 + М cos Ht) sin(wot + ф0).
При фазе ф0 = 0, путем тригонометрического преобразование произведение может быть приведено к виду: 3
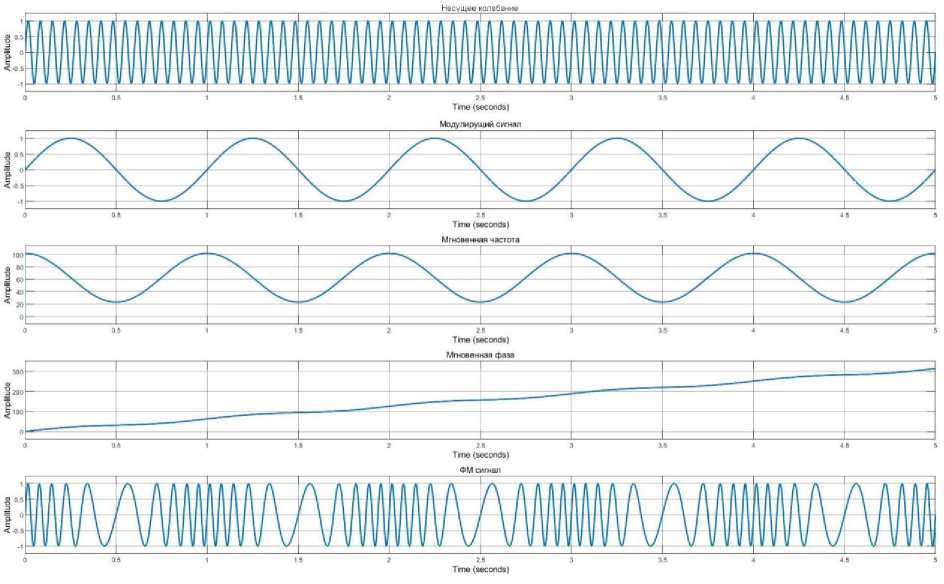
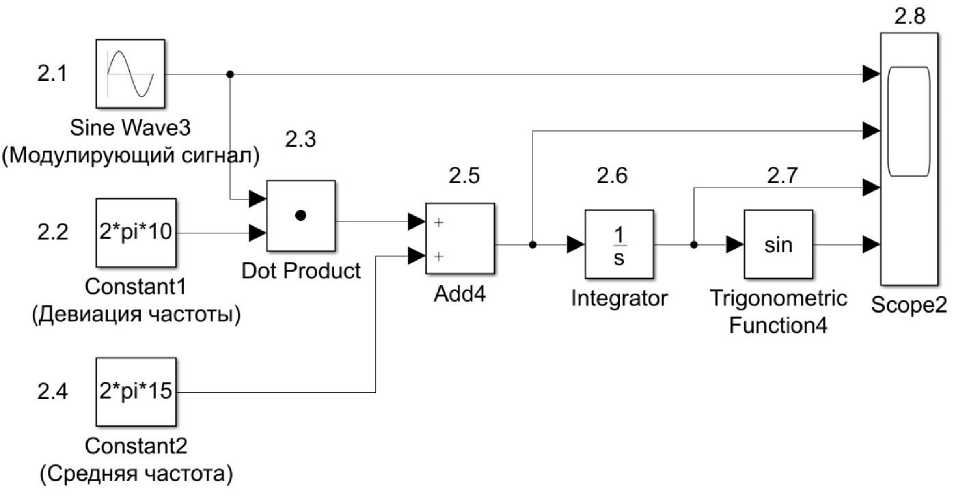
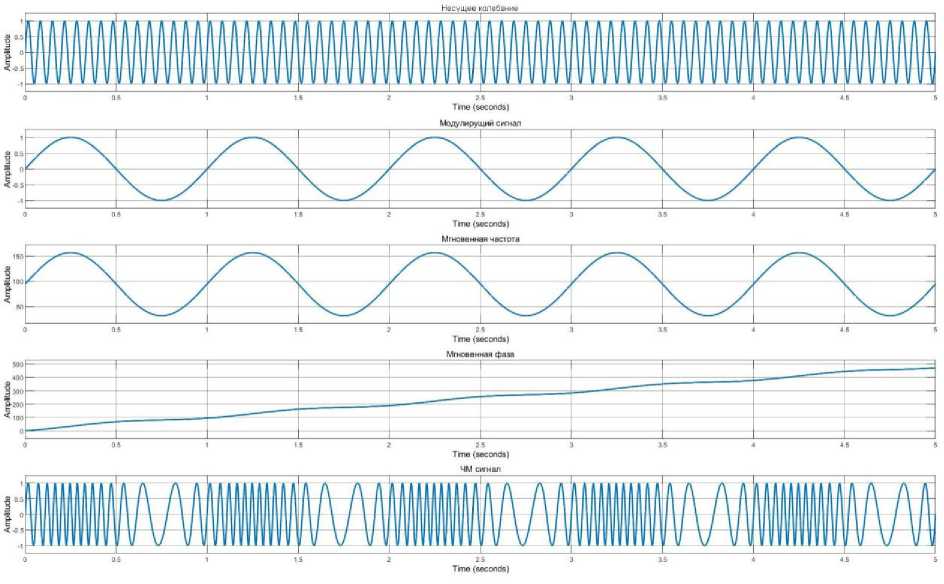
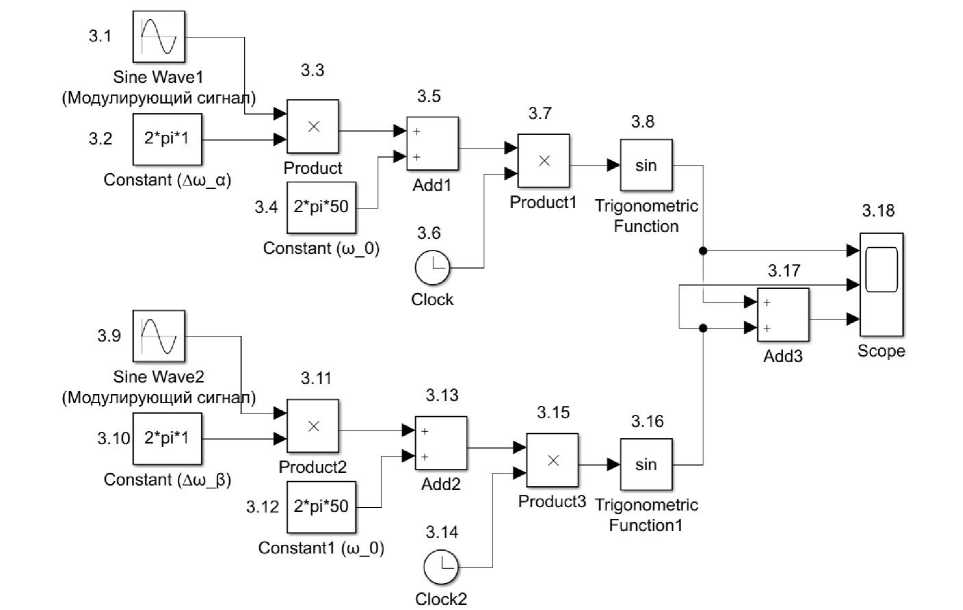
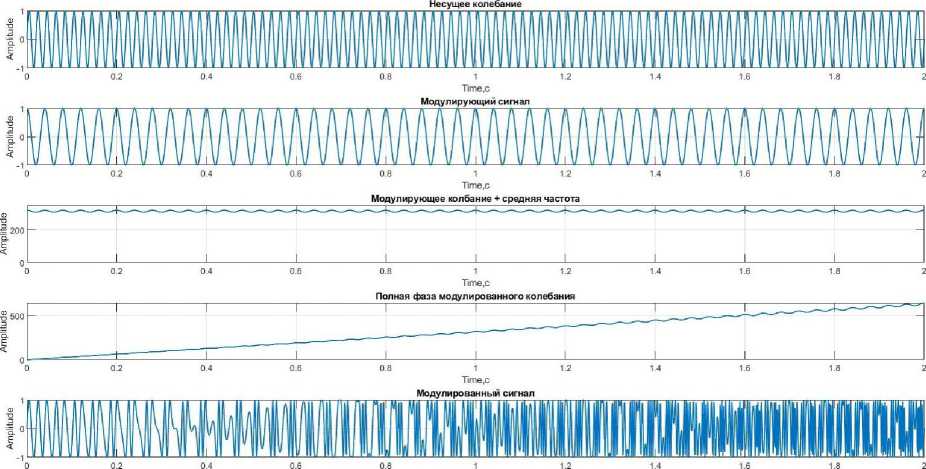
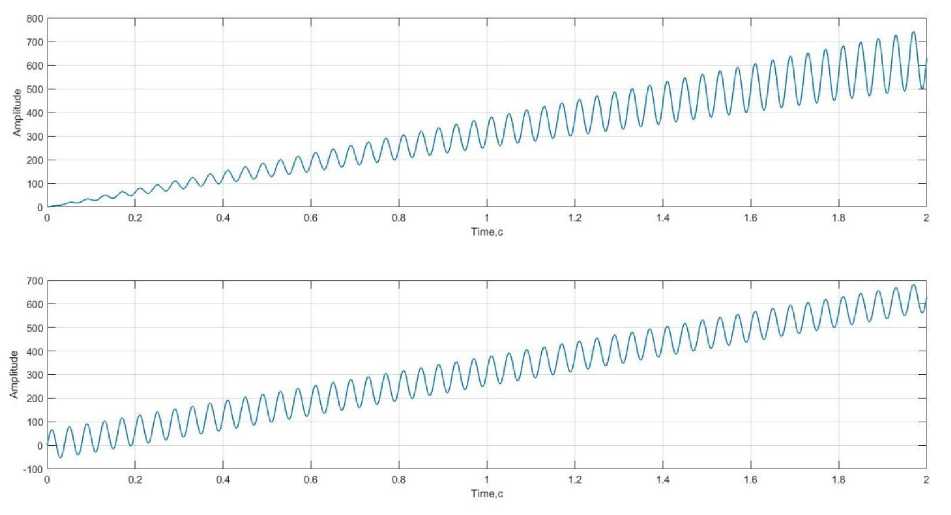
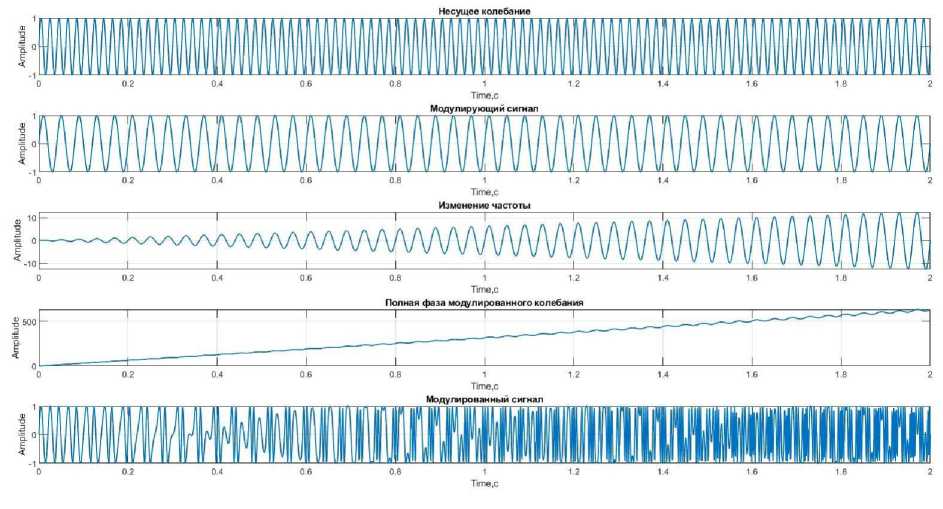
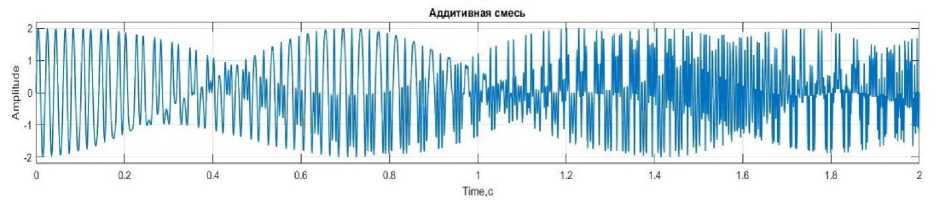
пАМ = U0 sin a)0t + ^^0sin(ca0 + П) t + ^°sin( Угловая модуляция (УМ). При УМ изменяется полный угол (0) несущего колебания. УМ может быть реализована: с помощью фазовой модуляции, когда фаза изменяется в соответствии с изменением амплитуды модулирующего сигнала; частотной модуляции, когда частота несущей изменяется пропорционально амплитуде модулирующего сигнала. Полная фаза: 0 = w0t + kb(t). Круговая частота по определению представляет собой скорость изменение начальной фазы. Мгновенная частота - это производная полной фазы по времени: mW) — т,., + ~. at 0 at Тогда полная фаза [4, с. 525]: 0 = f w(t) dt. Фазовая модуляция (ФМ). ФМ является прямым нелинейным видом модуляции сдвиг фазы ф изменяется от начального значения ф0 пропорционально модулирующему сигналу b (находится под знаком тригонометрической функции): Фн = Ф0 + kb(t), где к - размерный постоянный коэффициент пропорциональности, b(t) - модулирующий сигнал. b(t) = U sin(^t + фм), Фн = Ф0 + k(U sin(Ht + фм)), «фм = Uh sinC^t + Ф0 + k(U sin(Ht + Фм))), т = kU - индекс ФМ, равен максимальному отклонению начальной фазы колебания от среднего значения ф0. При фазе ф0 = 0. аФМ = Uh sin(^0t + т sin(Qt + фм)). Частотная модуляция (ЧМ). При ЧМ частота to(t) изменяется относительно среднего значения (to0), пропорционально модулирующему сигналу b(t). ЧМ является нелинейным интегральным видом модуляции, т.к. её можно представить, как ФМ, у которого фаза изменяется пропорционально не модулирующему сигналу, а интегралу от него. В ЧМ частота изменятся по закону: ^(t) = ш0 + kb(t), где к - размерный постоянный коэффициент пропорциональности, b(t) - модулирующий сигнал. b(t) = U cos(Ht + фм) цЧМ = UH sin J ^(t) tit = Um sin J (ш0 + kb(t)) tit = UH sin(^0t + C + J kb(t)) tit, где C = ^0 - постоянная интегрирования, играет роль начальной фазы [5, с. 13]. цЧМ = UH sin(^0t + ^0 + J U cos(Ht + фм)) tit = UH sin(^0t + ^0 + ^sin(Ht + фм)), m = ~~ = ~Д — девиация частоты (индекс ЧМ). При фазовом угле ф0 = 0: пЧМ = UH sin(^0t + m sin(Ht + ^м)), где ш0 - средняя частота колебания (немодулированная частота), H -частота модуляции [4, с. 75]. Для краткости положим, что ^м = 0, тогда уравнения для ЧМ и ФМ имеют вид: аФМ = UH sin(w0t + msinHt), нЧМ = UH sin(w0t + m sin Ht). Уравнения для ФМ и ЧМ, аналитическая форма аналогична [6, с. 102], отличаясь только индексом модуляции m. Ортогональная кодово-частотная модуляция (ОКЧМ). Способ ортогонально кодово-частотной модуляции предложен в диссертационной работе А.В. Авсиевичем. В отличии от стандартной ЧМ в ОКЧМ происходит изменение частоты Д со( t) sin Ht относительно среднего значения оз0. Несущее колебание: y(t) = UmsinC^Ht + ^H)- У которого частота изменяется по закону: ^н = ^0 + b(t), где ^w(t) - значения девиации частоты, b(t) - модулирующий сигнал. b(t) = A^(t) sin(Ht + фм). Тогда: ^н = С^0 + A^(t) sin(Ht + фм)')t, Учм = Um sin((^o + A^(t) sin(Ot + ^))t + ^0)• При фазе ф0 = фм = 0 уравнение принимает вид: уЧМ = Um sin((^0 + A^(t) sinHt)t). Раскрыв скобки получим уравнение, частотной модуляция с синусоидальной модулирующей частотной: у1 = Um sin(^0t + Ama(t)t sin Ht). Аналогично формируется частотная модуляция с косинусоидальной модулирующей частотной, итоговое уравнение которой: у2 = Um sin(^0t + A^(t)tcosHt), Ортогональный кодово-частотный модулятор описывается уравнением: у = Umsin(w0t + Awa(t)tsinHt) + Umsin(^0t + A^^(t)tcosHt), где ta0 - средняя частота, Um - амплитуда модулируемого сигнала, П - частота модулирующего сигнала, Awa(t)u A^(t) - значения девиации частоты [7, с. 38]. Модель генератора для формирования фазово-модулированного сигнала Рис. 1. Модель генератора ФМ сигнала блок 1.1 «Sine Wave» – генератор синусоидального сигнала (генерирует модулирующий синусоидальный сигнал sin nt); блок 1.2 «Constant» – источник постоянного воздействия задает константу или вектор констант девиации фазы (т); блок 1.3 «Product» - блок умножения (т sin nt); блок 1.4 «Constant» - источник постоянного воздействия задает константу или вектор констант средней частоты (to0t); блок 1.5 «Clock» -источник текущего времени служит для генерации чисел, которые являются значениями текущего времени моделирования (t); 1.6 «Product» -7 блок умножения (to0t); блок 1.7 «Add» - блок сложения для вычисления полной фазы несущего колебания (w0t и m sin nt); блок 1.8 «Trigonometric Function» – блок вычисления тригонометрических функций от полной фазы (m0t + m sin nt); блок 1.9 «Scope» - осциллограф для наблюдения временных и иных зависимостей; блок 1.10 «Derivative» – дифференцирующий блок для вычисления w(t). На рисунке 2 представлен результат работы модели генератора ФМ сигнала, графики: 1) несущий сигнал UHsin(wHt); 2) модулирующий сигнал sin nt; 3) изменение мгновенной частоты w(t) = w0+^^; 4) изменение мгновенной фазы ^н = ^0 + kb(t); 5) итоговый ФМ сигнал Um sin(^0t + m sin nt). Рис. 2. Временные диаграммы процесса формирования синусоидальной ФМ сигнала Изменение мгновенной фазы несущего колебания повторяет закон изменения модулирующего колебания (линейное изменение фазы накладывается переменное приращение). Изменения мгновенной частоты несущего колебания определяется производной [8, c. 72]. Модель генератора для формирования частотно- модулированного сигнала Рис. 3. Модель генератора ЧМ сигнала Для формирования модулированного сигнала разработаны в ПП Matlab Simulink блоки генератора ЧМ (рисунок 3): блок 2.1 «Sine Wave» – генератор синусоидального сигнала (генерирует модулирующий косинусоидальный сигнал cos Qt); блок 2.2 «Constant» – источник постоянного воздействия задает константу или вектор констант (к); блок 2.3 «Product» - блок умножения к cos Qt; блок 2.4 «Constant» – источник постоянного воздействия задает константу или вектор констант средней частоты (<у0); блок 2.5 «Add» - блок сложения 9 средней частоты и модулирующего сигнала (to0 и к cos fit); блок 2.6 «Integrator» - блок интегрирования входных данных волной фазы J (ш0 + kb(t))dt; блок 2.7 «Trigonometric Function» - блок вычисления тригонометрических функций от результат интегрирования (^0t + т sin fit); блок 2.8 «Scope» - осциллограф для наблюдения временных и иных зависимостей. На рисунке 4 (результат работы модели генератора ЧМ сигнала) представлены графики: 1) несущий сигнал Umsin(w0t); 2) модулирующий сигнал sin fit; 3) изменение мгновенной частоты ш; 4) произведение индекса и модулирующего сигнала: Awa(t)t sin fit; 5) итоговый частотно модулированный сигнал Um sin(w0t + Awa(t)tsinfit). Рис. 4. Временные диаграммы процесса формирования синусоидальной ЧМ сигнала Изменения мгновенной частоты несущего колебания повторяет изменения модулирующего сигнала. Девиация частоты пропорциональна амплитуде модулирующего колебания. Изменения мгновенной фазы несущего колебания определяется интегрированием [8, c. 73]. Модель генератора для формирования ортогонально кодовочастотного модулированного сигнала Рис. 5. Модель генератора ОКЧМ сигнала Для формирования модулированного сигнала разработаны в ПП Matlab Simulink блоки генератора ОКЧМ (рисунок 5): блок 3.1 «Sine Wave» - генератор синусоидального сигнала (sinHt, cos Ht, генерирует модулирующий синусоидальный или косинусоидальный сигнал); блок 3.2 «Constant» – источник постоянного воздействия задает константу или вектор констант для (A ta0); блок 3.3 «Product» - блок умножения; блок 3.4 «Constant» - источник постоянного воздействия задает константу или вектор констант для (ш0); блок 3.4 «Constant» – источник постоянного воздействия задает константу или вектор констант величины (са0); блок 3.5 «Add» - блок сложения щ0 и A^a(t) sin Ht; блок 3.6 «Clock» - источник текущего времени служит для генерации чисел, которые являются значениями текущего времени моделирования (t); блок 3.8 «Trigonometric Function» - блок вычисления тригонометрических функций от (w0t + A^a(t)t sin Ht) или (w0t + A^(t)t cos Ht); блок 3.17 «Add» – блок сложения синусоидальной и косиусоидальной составляющей ОКЧМ сигнала; блок 3.18 «Scope» – осциллограф для наблюдения временных и иных зависимостей. Для упрощения исследования примем произведение девиации частоты и времени равной m: Awa(t)t = m. Рассмотрим процесс формирования синусоидальной составляющей (по аналогии с процессом формирования угловой модуляцией) сигнала ОКЧМ. На рисунке 6 (результат работы модели генератора ОКЧМ сигнала) представлены графики: 1) несущее колебание Cmsin(w0t); 2) модулирующий сигнал sinHt; 3) изменение частоты Awa(t)t sin Ht; 4) полная ваза модулированного колебания w0t + Awa(t)t sin Ht; 5) итоговый частотно модулированный сигнал Um sin(^0t + Awa(t)t sin Ht). Time,с Рис. 6. Временные диаграммы процесса формирования синусоидальной составляющей ОКЧМ сигнала Наглядо отличие ЧМ от ОКЧМ можно увидеть на рисунке 7, амплитуда колебния полной фазы ОКЧМ сигнала постоянно возрастает со временем, амплитуда мнгновенной фазы ЧМ остается постоянной. Графики 1) полная фаза ОКЧМ сигнала; 2) мнгновенная фаза ЧМ сигнала. Рис. 7. Временные диаграммы процесса изменения полной фазы несущего колебания В отличии от стандартной ЧМ в ОКЧМ происходит изменение частоты Д6)a(t)sinПt около среднего значения ю0. Рассмотрим трансформацию сигнала в этом случае. Сигнал с косинусоидальный модулирующей частотой у2 = Um sin()0t + Дa)p(t')t cos Ht). После преобразования уравнение принимает вид Um sin()0 + A)^(t) cos Ht)t. В таком случае графики процесса формирования косинусоидальной составляющей ОКЧМ сигнала будут принимают вид, представленный на рисунке 7: 1) несущее колебание Um sin()0t); 2) модулирующий сигнал cosHt; 3) сумма модулирующего колебания и средней частоты (колебание около среднего значения): )0 + Дшa(t)t cos H; 4) полная фаза модулированного колебания ()0 + A)a(t)t cos H)t; 5) итоговый частотно модулированный сигнал Um sin()0 + Д) (t) cos Ht)t. Рис. 7. Временные диаграммы процесса формирования косинусоидальной составляющей ОКЧМ сигнала Итоговый график ортогонального кодово-частотного сигнала, который представляет собой аддитивную смесь представлен на рисунке 8. Рис. 8. Временные диаграммы процесса формирования ОКЧМ сигнала Заключение Результатом проделанной работы является исследование процесса формирования ортогонального кодово-частотно модулированного сигнала, сравнение с частотной модуляцией и фазовой модуляцией. Представлены временные диаграммы изменения параметров несущего колебания в процессе его формирования с помощью программного комплекса Matlab Simulink. Наглядно приведены отличия ОКЧМ от стандартной ЧМ, выражаемой в законе изменения мгновенной фазы колебания при ФМ (ЧМ) и частоты при ОКЧМ.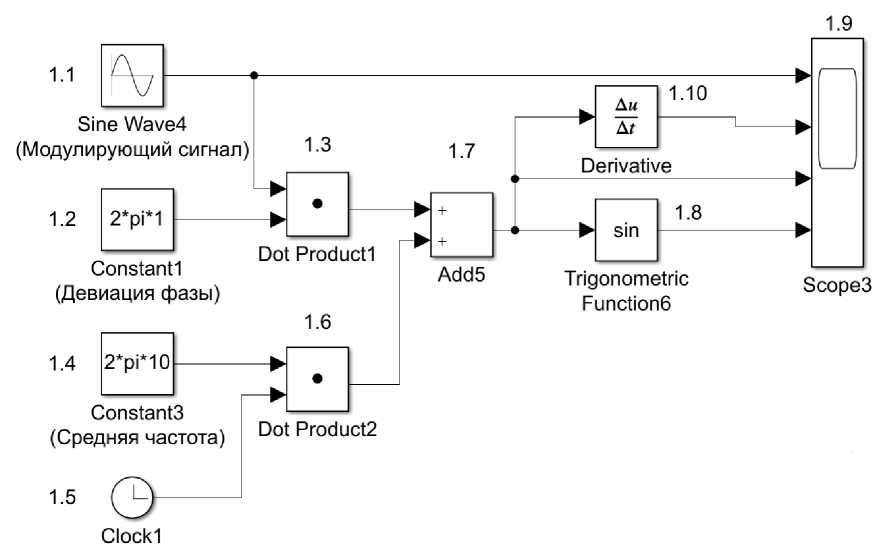
Список литературы Сравнение процесса формирования ортогональной кодово-частотной модуляции и угловой модуляции в пакете MATLAB Simulink
- Дьяконов В. П. Simulink 5/6/7: Самоучитель. - М.: ДМК_Пресс, 2008. - 784 с.
- Рид Р. Основы теории передачи информации. М: Вильямс, 2004. 304 c.
- Горелов Г. В. Теория передачи сигналов на железнодорожном транспорте: учебник. М.: УМЦ ЖДТ, 2013. - 532 с.
- Сергиенко А. Б. Цифровая обработка сигналов: учеб. пособие. - 3-е изд. - СПб.: БХВ-Петербург, 2011. - 768 с
- Гоноровский И. С. Частотная модуляция и ее применения. М: Связьиздат, 1948. - 285 с.
- Баскаков С. И. Радиотехнические цепи и сигналы: учеб. для вузов по специальности "Радиотехника" / С.И. Баскаков. - Изд. 5-е, стер. - М.: Высш. школа, 2005. - 462 с.
- Авсиевич А. В. Разработка метода идентификации нестационарных процессов с ортогональной кодово-частотной модуляцией: диссертация кандидата технических наук: Братск, 2002. - 118 с.
- Теория электрической связи: учебное пособие / К.К. Васильев, В.А. Глушков, А.В. Дормидонтов, А.Г. Нестеренко; под общ. ред. К.К. Васильева. - Ульяновск: УлГТУ, 2008. - 452 с.


