Сравнение результатов решения задачи механики разрушения для трубы с несквозной трещиной

Причиной опасного состояния, а в отдельных случаях и разрушения трубопроводных систем, предназначенных для транспортировки углеводородов, как правило, является наличие острых трещиноподобных дефектов технологического или эксплуатационного происхождения [1, 2]. Наибольший интерес здесь представляют несквозные и в первую очередь (учитывая сравнительно малую толщину стенки трубы) поверхностные трещины. Такие дефекты имеют пространственный характер и в общем случае являются многопараметрическими. Современными методами эксплуатационного неразрушающего контроля полную исчерпывающую информацию о выявленном дефекте удается получить лишь в некоторых отдельных случаях. В связи с этим в отечественной и зарубежной практике при неполноте информации о дефекте, а также для упрощения расчетных методик дефекты принято аппроксимировать трещиной полуэллиптической формы [3–16].

В настоящей статье рассматривается стальная труба 220×10, ослабленная несквозной полуэллиптической трещиной осевой ориентации, располагающейся на наружной поверхности. Размеры дефекта приняты следующими: глубина l = 5 мм; полудлина a = 10 мм. Труба находится под действием внутреннего давления p = 5 МПа. Здесь выбрана достаточно толстостенная труба малого диаметра для усиления эффекта влияния кривизны оболочки на получаемые результаты.

Решение задачи механики разрушения проводится в CAE-системе ANSYS с использованием программ-макросов, описанных в работе [17]. Моделируемый фрагмент стенки трубы с трещиной представлен на рис. 1.

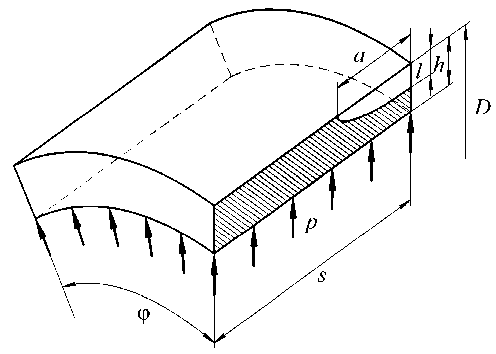
Рис. 1. Фрагмент трубы с осевой наружной трещиной:

2 s

5 = 4max ( l,a ) ; ф = —

Нагружение здесь осуществляется давлением р , которое прикладывается к внутренней поверхности трубы. В качестве граничных условий выступают условия симметрии, наложенные на все боковые грани рассматриваемого фрагмента. При этом они не оказывают какого-либо влияния на напряженно-деформированное состояние в области рассматриваемого дефекта, поскольку размеры фрагмента 5 и ф являются достаточно большими.

Конечно-элементная разбивка в окрестности трещины показана на рис. 2. Следует отметить, что использование здесь регулярной радиальной сетки в объеме, окружающем фронт трещины, обеспечивает высокую точность вычисления параметров механики разрушения.

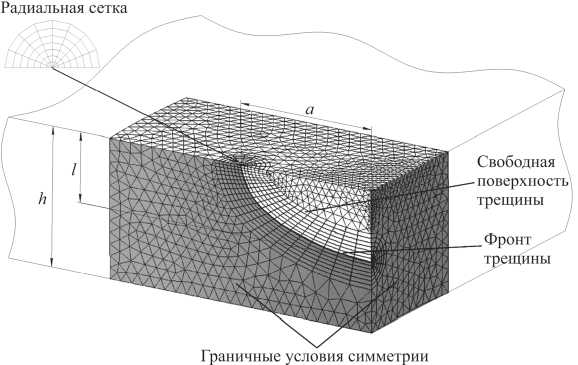
Рис. 2. Разбивка на конечные элементы

Расчет значений коэффициента интенсивности напряжений вдоль фронта дефекта выполняется по формуле

—..( ( о ) , 1 -Ц ²

где E и ц - модуль упругости и коэффициент Пуассона материала трубы; J ( 0 ) - значения J -интеграла в точках фронта, определяемые численно методом интегрирования по области, который в настоящее время является наиболее точным при конечно-элементном моделировании; 0 - угловая координата точки линии фронта [17].

Следует отметить, что в литературе содержится значительное количество формул для вычисления коэффициентов интенсивности напряжений в трубах и сосудах давления с поверхностными трещинами.

Так, в работах [18, 19] для расчета K _I вдоль фронта продольной несквозной полуэллиптической трещины в цилиндрической оболочке, нагруженной внутренним давлением, приводится следующее выражение:

^|(0)=

iR. ^ C h C c h Ф

(           1 2          Г 0,25

sin² 0+— 2-cos² 0

I        a       )

где R _o и h – соответственно наружный радиус и толщина оболочки.

Под Ф здесь понимается полный эллиптический интеграл второго рода, вычисляемый по формуле п2 /   a 2 -12                            ( l\X65

Ф = f J1-- 2— sin ² ф d ф = , 1 + 1,464 1 — 1

О V a              У        I a)

В выражении (1) величина C_h представляет собой поправку на геометрию трещины и определяется как

C h =

1 + 0,122 ⁽ 1 - — |

( 2 a )

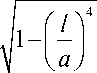
а величина C_c имеет смысл поправки на кривизну и толщину оболочки и вычисляется по следующей формуле:

C c = [ 0,481 a+ 0,386 e

^{1,25 a} + 0,614 - 1 1 - - 1, , ^J h

a ²

где a = R-h^12(1 -Ц2) - безразмерный параметр, характеризующий относительную длину трещины.

Другая наиболее используемая и опробованная формула вычисления коэффициентов интенсивности напряжений для цилиндрических сосудов давления с продольной несквозной полуэллиптической трещиной на внутренней или наружной поверхности имеет следующий вид [20]:

K I ( e ) = 0,97 / c F ( 9 ) CT

n a

Q ^,

где f_c – поправка на кривизну оболочки, вычисляемая по формулам [21, 22]:

– для трещины на внутренней поверхности

/ c =

R o ² + R-

R o - R i

+ 1 - 0,5

g 1 h N h R.’

– для трещины на наружной поверхности

fc =

R ² + R ² o i

R ² - R ² o i

- 1 + 0,5

g 1 h_

N h R/

причем R_i и R _o – внутренний и наружный радиусы соответственно.

В формуле (2) под о понимается среднее окружное напряжение

о =

p (Ro + R)

2 h

Величина Q находится по формуле

1,65

Q = 1 + 1,464 | ^— I

V a )

= Ф ².

И, наконец, функция F ( 0 ) определяется как

F (0) =

M 1 + M ₂

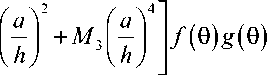
где

M 1 = 1,13 - 0,09 ^- ;

a

0,89

M₂ = - 0,54 +-- г- ;

0,2 + l

a

• 1    -Ц ;

a)

a

₂                         0,25

cos² 0+ sin² 0

;

g ( 0 ) = 1 + 0,1 + 0,35

Для поверхностных наружных полуэллиптических трещин осевой ориентации в цилиндрических сосудах в работе [23] для вычисления коэффициентов интенсивности напряжений в точках фронта дефекта приводится следующее выражение:

^K I    ^iF e (⁶) ,

где Q находится по формуле (3); F_e – корректировочный коэффициент, определяемый как

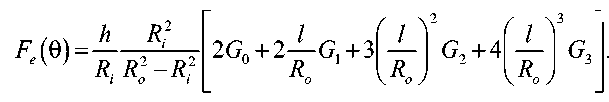
Здесь G_j – коэффициенты влияния, значения которых представлены в таблицах, приведенных в работе [23].

Европейский стандарт SINTAP [24] и созданная в Великобритании методика оценки дефектов R6 [25] для вычисления коэффициентов интенсивности напряжений в отдельных точках фронта продольной полуэллиптической трещины на наружной поверхности бесконечно длинной трубы используют следующую формулу:

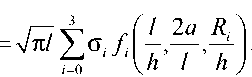
где о i - коэффициенты разложения окружных напряжений в неповрежденной части трубы в ряд

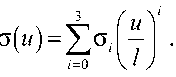
^о( и ) = 2 о i = 0

Здесь u – координата, отсчитываемая от наружной поверхности трубы в направлении глубины дефекта (пределы изменения 0 <  и <  l ).

Коэффициенты f_i в формуле (5) представляют собой табулированные функции, зависящие от геометрических параметров трубы и дефекта. Для наиболее глубокой точки трещины и точек вблизи выхода дефекта на наружную поверхность значения коэффициентов приведены в стандарте [24].

Сравнение различных решений приведено на рис. 3, где показано распределение параметра K _I по всему фронту рассматриваемой полу-эллиптической трещины. Здесь сплошная линия 1 представляет наше решение, кривые 2 , 3 и 4 построены с использованием соответственно выражений (1), (2) и (4), а кружочками отмечены результаты, рассчитанные по формуле (5).

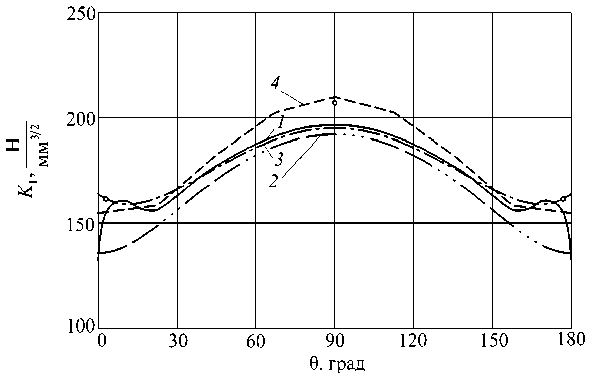
Рис. 3. Распределения коэффициента интенсивности напряжений вдоль фронта трещины

Как видно, наше решение, полученное при помощи CAE-системы ANSYS, хорошо согласуется с результатами других авторов. При этом применение регулярной сетки с большим числом элементов вдоль фронта дефекта существенно повышает точность вычисления параметров механики разрушения и позволяет выявить наличие краевых эффектов в виде локальных максимумов, расположенных вблизи выхода трещины на поверхность трубы. Значения в этих точках выше, чем в концевых точках фронта, и именно их следует использовать для исследования роста трещины полуэллиптической формы при наличии пульсации давления. Как показывают результаты параметрических расчетов (в которых относительная глубина трещины lh варьировалась в диапазоне от 0,1 до 0,8 с шагом 0,1, а относительная длина дефекта la изменялась от 0,1 до 2,0 с тем же шагом), подобные краевые эффекты наблюдаются и при других размерах трещины. Это можно объяснить тем, что на свободной поверхности тела определяющим является плоское напряженное состояние, а внутри тела – плоская деформация. Переход от одного состояния к другому и приводит к появлению краевого эффекта.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ.